Výpis souhrnů
Elektromagnetická indukce
Podtémata
Elektromagnetická indukce
Pokud se v místě vodiče mění magnetické pole (je tzv. nestacionární), vyvolává tato změna vznik elektrického napětí (a následně i elektrický proud).
To je podstata elektromagnetické indukce. Mnohdy je tento efekt zanedbatelný, ale zejména pro prstence nebo smyčky vodiče může být za některých okolností velmi silný a může úplně nahradit existenci zdroje elektromotorického napětí v obvodu.
NahoruElektromagnetická indukce: základy
Každá změna magnetického pole vyvolává ve vodiči vznik elektrického napětí. To je elektromagnetická indukce. Důležitá je zejména pro prstence nebo smyčky vodiče, které se tak mohou začít chovat jako zdroj elektromotorického napětí. A když je závitů vodiče víc, jako u cívky, celý efekt (velikost napětí) se násobí.
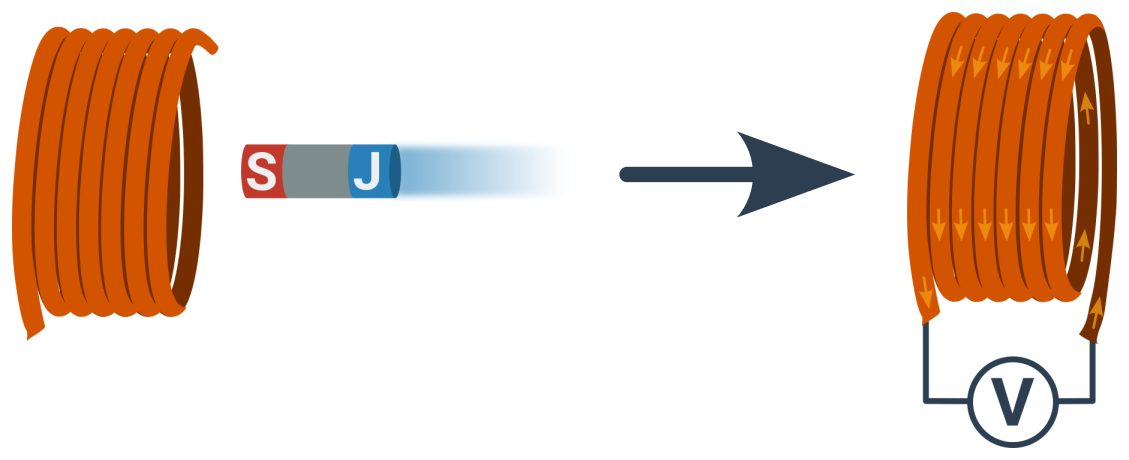
Podle Faradayova zákona vzniká ve smyčce indukované elektrické napětí U_\mathrm i úměrné rychlosti změny magnetického pole. Typickým příkladem je pohyb permanentního magnetu poblíž namotané cívky vodiče, vyvolat ji ale může i elektromagnet (druhá cívka pod proudem, viz transformátory).
Pro onen magnet a cívku je indukované napětí úměrné:
- síle magnetu (velikosti jeho magnetické indukce B)
- rychlosti pohybu magnetu
- počtu závitů cívky
Příklad: Různé cívky
- Jedna cívka má 5 závitů a druhá (stejně velká) 10 závitů.
- Druhá cívka tedy za stejných podmínek indukuje 2krát větší napětí.
Příklad: Různě rychlý pohyb
- Máme tři stejné cívky, stejně daleko od magnetu.
- K první cívce se k magnet blíží 1 m/s, ke druhé 1 cm/s a vůči třetí se nepohybuje.
- První cívka tedy indukuje 100krát větší napětí než druhá.
- Indukované napětí třetí cívky je nula.
Protože je napětí úměrné okamžité změně magnetického pole, jakmile se magnetické pole přestane měnit, indukované napětí klesne zase na nulu.
Princip elektromagnetické indukce se používá v elektrárnách ke generování střídavého napětí, i jeho transformaci na 230 V do našich zásuvek. Založeno je na ní ale mnoho dalších vynálezů – od indukčních vařičů po dynamické mikrofony.
NahoruElektromagnetická indukce: vzorce a vztahy
Elektromagnetickou indukci a indukované napětí můžeme popsat kvantitativně pomocí Faradayova zákona. Potřebujeme ale rozumět magnetickému indukčnímu toku.
Magnetický indukční tok
Vyjadřuje, kolik magnetického pole právě prochází nějakou plochou – např. průřezem smyčky vodiče. Značíme jej \Phi a jednotkou je weber.
Intuitivně si jej můžeme představit jako množství magnetických indukčních čar, které procházejí skrz smyčku (a vracejí se vnějškem). Zřejmě tedy záleží na velikosti B (obvykle jej znázorňujeme právě hustotou čar), velikostí plochy S a orientací S vůči směru B. Předpokládáme, taky že je B v rovině této smyčky alespoň přibližně homogenní. A to je vlastně celé – B, S a úhel. Přesný vzorec záleží na tom vůči, čemu tento úhel vztahujeme (jestli k rovině smyčky nebo ke kolmici na ni). Více v obrázku.
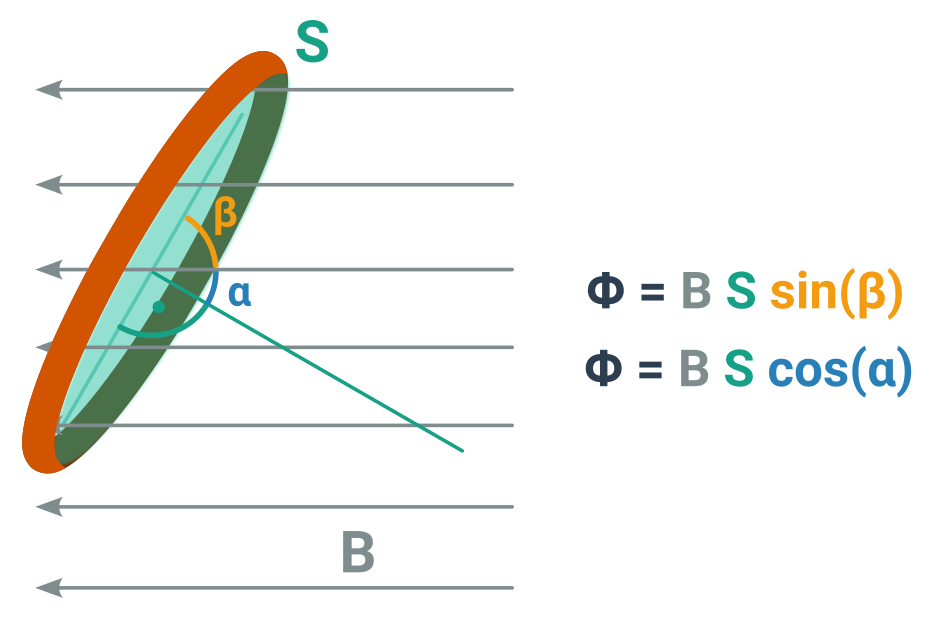
Pokud míří B kolmo na smyčku, dostaneme každopádně \cos 0° resp. \sin 90° (tedy jedničku) a tok je:
\Phi=B\cdot S
a pokud jdou rovnoběžně, dají goniometrická funkce nulu a tok je nulový.
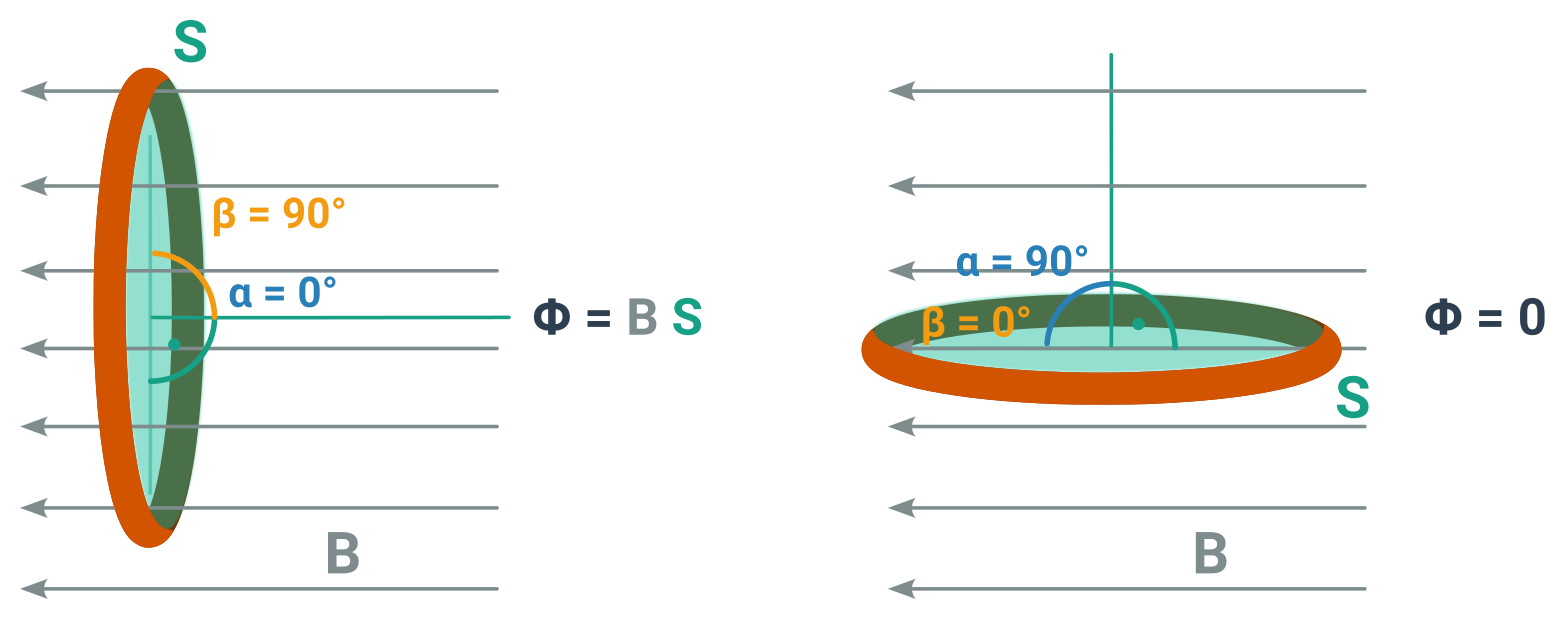
Faradayův zákon
Indukované napětí U_\mathrm i je rovno mínus změně magnetického toku za změnu času:
U_\mathrm i=-\frac{\Delta \Phi}{\Delta t}
Příklad: Přibližující se magnet
- K vodivé smyčce se přibližuje magnet:
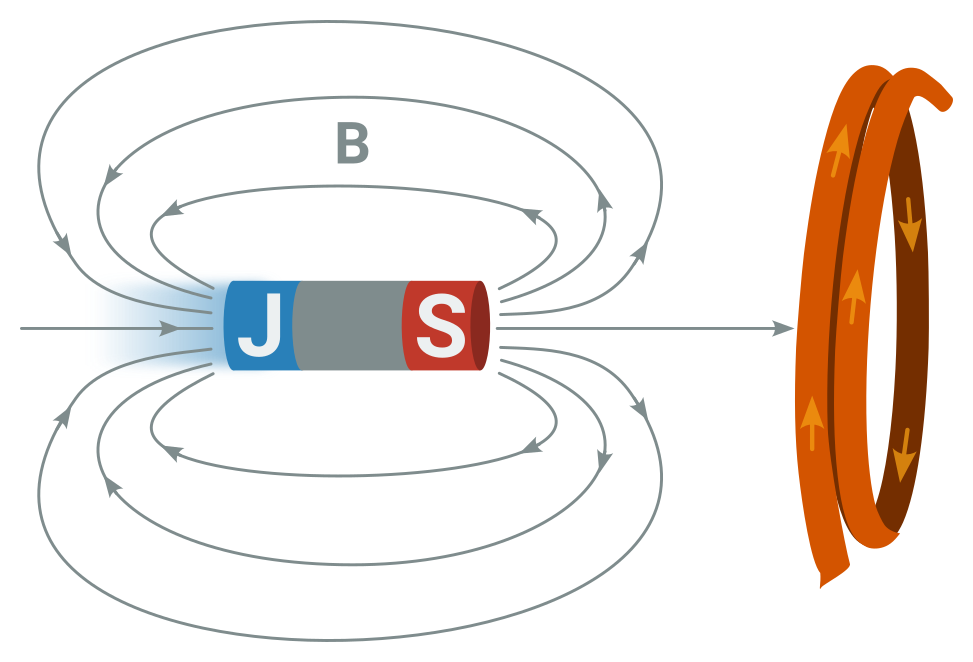
- Smyčkou prochází čím dál tím více indukčních čar, roste magnetický tok \Phi.
- Za poslední 0,1 s (\Delta t) je rozdíl magnetického toku 0,2 Wb (\Delta\Phi).
- Dosadíme to do U_\mathrm i=-\frac{\Delta \Phi}{\Delta t}=-\frac{0{,}2}{0{,}1}\,\mathrm{V}.
- Během poslední 0,1 s bylo tedy indukované napětí (průměrně) −2 V.
Příklad: Kdy je během průletu magnetu okamžité \,U_\mathrm i \, nulové?
- K vodivé smyčce se přibližuje magnet a projde jí skrz:

- Okamžité U_\mathrm i je úměrné okamžité změně magnetického toku.
- Tok se nemění jen když je konstantní, nebo v okamžicích svého maxima nebo minima.
- Dokud se magnet přibližuje, magnetický tok \Phi roste.
- Po průchodu smyčkou se magnet vzdaluje a \Phi klesá.
- Nejvyšší magnetický tok tedy bude, když je magnet uprostřed smyčky. A právě tehdy bdue indukované napětí procházet nulou.
Příklad: Rotující prstenec v neměnném magnetickém poli
- Vodivý prstenec se otáčí v magnetickém poli. Za čas t se otočí o čtvrtinu:

- Na levém obrázku je tok \Phi roven BS.
- Na pravém obrázku je tok \Phi roven 0.
- \Delta\Phi je tedy -BS.
- \Delta t je přímo čas t ze zadání.
- Průměrné indukované napětí během tohoto pootočení je tedy U_\mathrm i=-\frac{\Delta \Phi}{\Delta t}=-\frac{-BS}{t}=\frac{BS}{t}.

