Pohyb po kružnici

Z nepřímočarých pohybů je nejdůležitější rovnoměrný pohyb po kružnici. Popisuje situace jako točení na kolotoči, prádlo v bubnu ždímačky nebo otáčení planety Země. Přibližně odpovídá i řadě složitějších situací (např. pohyb v trolejbusu v zatáčce).

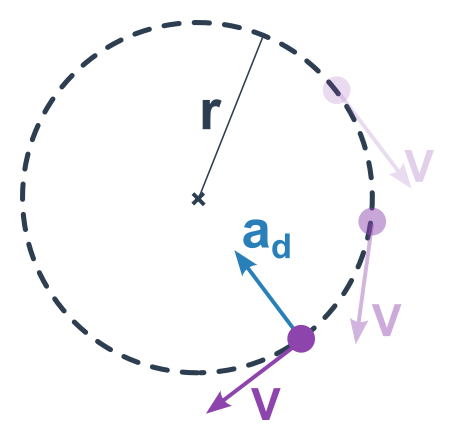
Tedy trajektorií je kružnice. Rychlost v je tečnou k trajektorii (i proto se nazývá obvodová) a má konstantní velikost, mění se ale směr. Zrychlení (které právě popisuje změny směru rychlosti) směřuje do středu kružnice. Říká se mu proto dostředivé a značíme jej a_\mathrm d. Má velikost:

a_\mathrm d=\frac{v^2}{r}

Často nás nezajímá, jak rychle se pohybujeme, ale jak rychle se otáčíme dokola (úhel za jednotku času). Proto definujeme úhlovou rychlost \omega. Pro rovnoměrný pohyb po kružnici je \omega konstantní a úhel otočení \varphi je přímo úměrný času.

Platí vztahy jako \omega=\frac{v}{r} resp. v=\omega\cdot r. Po dosazení za v tak můžeme dostat alternativní vztah pro a_\mathrm d:

a_\mathrm d=\omega^2\cdot r