Výpis souhrnů
Tělesa a látky
Podtémata
Co je těžší? Kilo železa, nebo kilo peří?
Komu někdy spadla na nohu železná činka, mohl by si myslet, že kilo železa je mnohem těžší. Ale kilogram a kilogram je stejná hmotnost. Liší se jen objemem.
Bylo by tedy dobré mít nějakou veličinu popisující, jak je něco těžké na jednotku objemu. A právě to je hustota. Značíme ji \rho, má jednotku kg/m³ a spočítá se přesně tak, jak jsme to řekli slovně – hmotnost dělíme objemem.
\rho=\frac{m}{V}
Na rozdíl od hmotnosti je hustota vlastností látek, a proto ji najdeme v tabulkách (např. hustota železa je kolem 7800 kg/m³ ať jde o hřebík nebo tank).
Příklad: dva materiály ze stejných částic
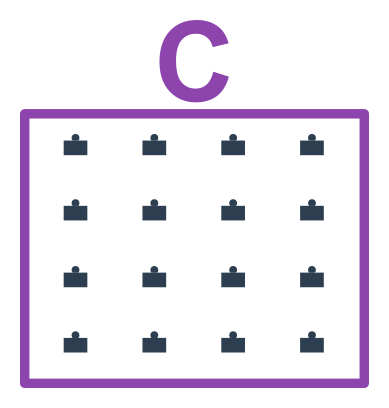
Dva materiály ze stejných (stejně těžkých) částic. Částice jsou ale různě nahuštěné. Proto platí \rho_A>\rho_B


Příklad: dva materiály ze stejně nahuštěných částic
Dva materiály ze stejně nahuštěných částic. Částice mají ale jiné hmotnosti. Proto platí \rho_A>\rho_C

Pokud chceme pomocí \rho=\frac{m}{V} počítat hmotnost nebo objem, můžeme (vztahový trojúhelník) dojít k tvarům m=\rho V a V=\frac{m}{\rho}.
Zajímavosti
Hustota může být i vlastnost tělesa (např. průměrná hustota mobilního telefonu).
Pokud již znáte Archimédův zákon, víte, že kilo peří je dokonce nepatrně těžší. Díky svému velkému objemu, je totiž při vážení na vahách nadlehčováno větší vztlakovou silou než kilo železa.
Skupenství
Látky kolem nás existují v mnoha formách. Pro ty nejzákladnější odlišnosti různých forem (schopnost držet stálý tvar nebo objem) se zavádí rozdělení na skupenství. Existují skupenství pevné, kapalné a plynné. Jako čtvrté skupenství se někdy označuje plazma.
Například látka jménem VODA se kolem nás běžně vyskytuje pevném (led), kapalném (voda z kohoutku) i plynném (vodní pára nad hrncem) skupenství.
Kapaliny a plyny označujeme souhrnně jako tekutiny.
Pevné skupenství
- stálý objem (nestlačitelné), stálý tvar a struktura (působením vnější síly ale je možná deformace/rozbití)
- částice látky jsou pevně provázány (vůči sobě se nepohybují, drží „formaci“)



Kapalné skupenství
- stálý objem (kapaliny jsou téměř nestlačitelné), proměnný tvar (přizpůsobuje se nádobě, ve které se nachází), je ohraničené (hladina rybníka, tvar kapky)
- částice látky na sebe slabě působí (ale vzájemně se pohybují)



Plynné skupenství
- snadno mění objem (vnější silou), proměnný tvar (přizpůsobuje se nádobě, ve které se nachází), nemá jasnou hranici
- částice látky se volně pohybují, jsou mezi nimi velké mezery, působí na sebe jen během srážek



Plazma
- skoro stejné jako plyn, ale některé částice jsou elektricky nabité (ionty a elektrony), vede tedy elektrický proud, obvykle svítí
- jde například o blesky, některé typy osvětlení, polární záři, ale i hvězdy nebo mlhoviny
- podle některých kritérií nejde o „opravdové“ skupenství



Přeměny skupenství
Pokud látce dodáváme, nebo odebíráme energii (např. ohříváme nebo ochlazujeme), může dojít ke změně jejího skupenství. Jednotlivé změny skupenství jsou znázorněny na diagramu níže:
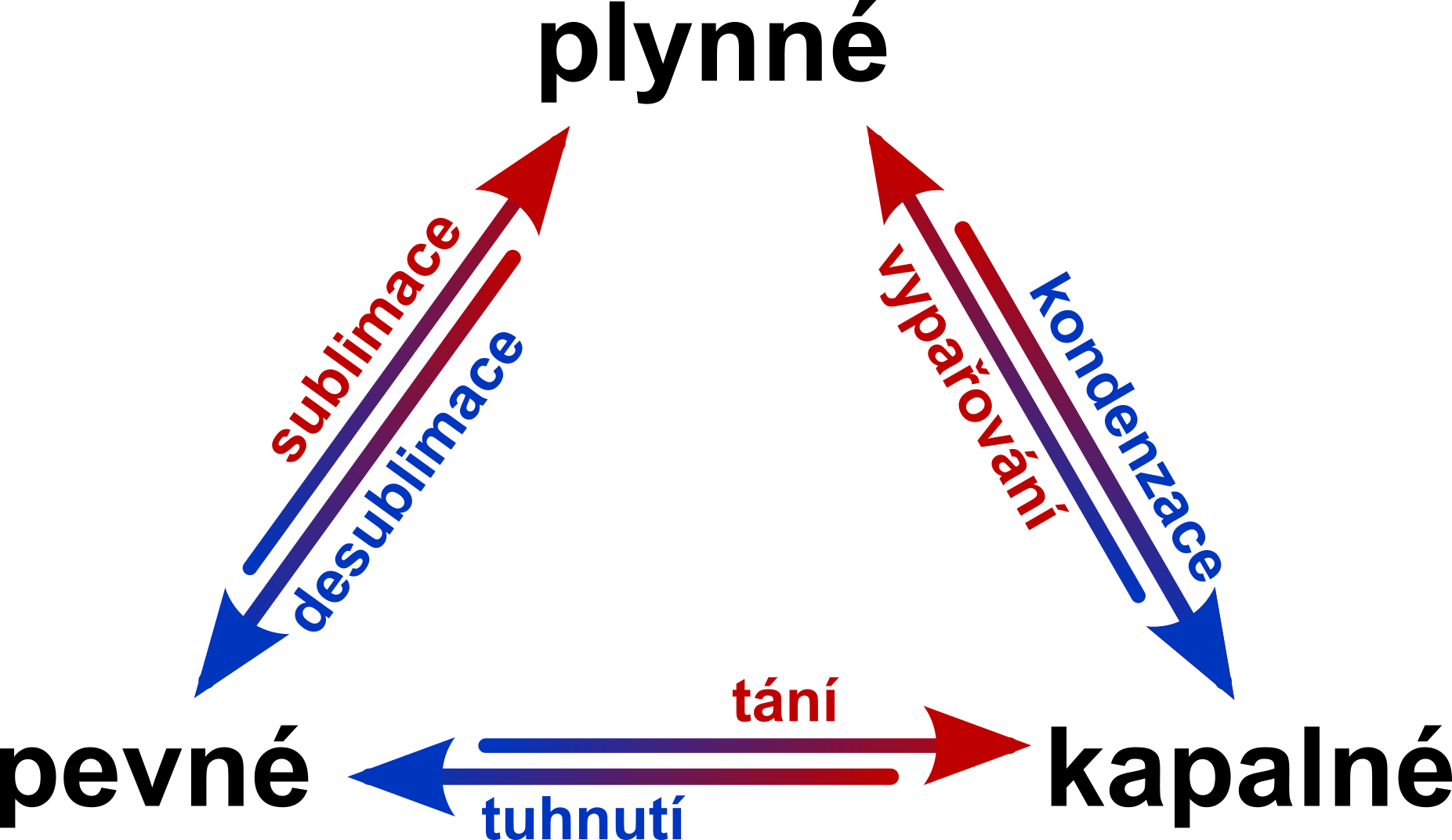
U přeměny kapaliny na plyn je dobře znám i pojem var. Jde o typ vypařování, kdy se kapalina přeměňuje na plyn v celém objemu (a ne pouze na svém okraji).
Tání, vypařování a sublimace spotřebovávají energii (musíme dodávat teplo). Při tuhnutí, kondenzaci a desublimaci se energie naopak uvolňuje. Tato energie souvisí se samotným procesem přeměny (ne se změnou teploty).
Příklad: od ledu k páře
Led (pevné) má −10 °C a zahříváme jej.
- Nejprve se ohřeje na teplotu tání 0 °C.
- Pak zůstává na 0 °C a teplo spotřebovává na přeměnu na vodu (tání).
- Tato voda (kapalné) se dále ohřívá až do 100 °C. Přitom se pomalu vypařuje.
- Zůstává na 100 °C a přeměňuje se na páru v celém objemu (var).
- Nakonec máme páru (plynné), která se může dále ohřívat (teoreticky neomezeně).
Pokud jde o plazma, to není skupenstvím v pravém slova smyslu, protože mezi plynem a plazmatem není ostrá hranice (změnu na plazma bychom ale mohli označit jako ionizaci plynu).
Zajímavosti
- Díky sublimaci cítíme například vůni pevného WC bloku.
- To, kdy nastane změna skupenství, je ve skutečnosti určeno jak teplotou, tak i okolním tlakem.
Struktura pevných látek
Podle struktury můžeme rozdělit pevné látky na krystalické (pravidelná struktura), amorfní (nepravidelná struktura) a polykrystalické. Na struktuře záleží i to jestli se látka chová ve všech směrech stejně. Taková látka je izotropní. Pokud tomu tak není (například kusy slídy se dobře lámou pouze v určitém směru), říkáme, že je látka anizotropní.
Krystalické látky
Částice jsou pravidelně rozmístěny v tzv. krystalové mřížce. Obecně mohou být anizotropní. Jde třeba o diamant, tuhu, krystalky síry, nebo led. 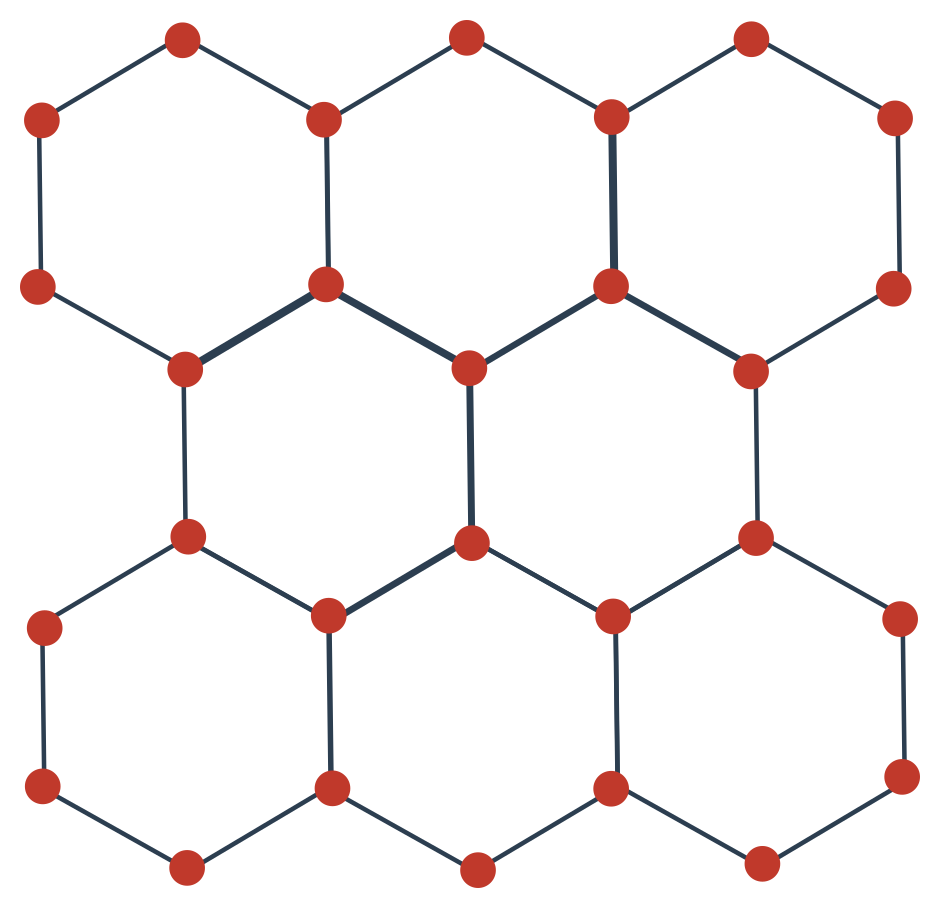
Amorfní látky
Částice nejsou v prostoru nijak uspořádány. Rozmístění je náhodné. I proto se látka vždy chová izotropně. Například jde o umělé látky, vosky nebo sklo.
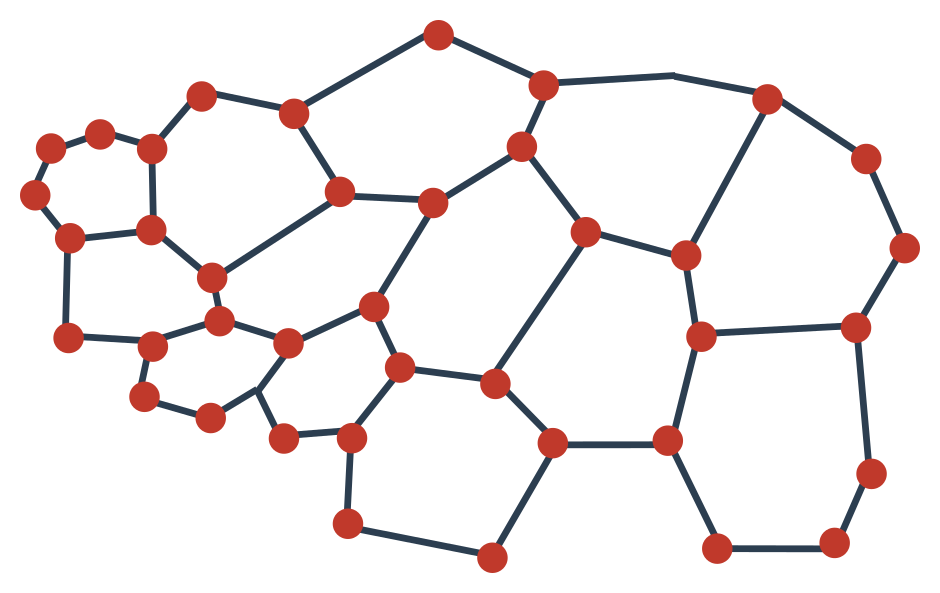
Polykrystalické látky
Jde o takový hybrid mezi předchozími. Mnoho malých pravidelných zrn (krystalků) naskládaných a natočených náhodně. Patří sem všechny kovy.
Základní typy krystalové mřížky
Nejmenším celkem mřížky je elementární buňka. Může mít různý tvar (podle toho rozlišujeme různé krystalické soustavy) a taky různé rozmístění částic. Prostá buňka mřížky je tvořena jen částicemi v jejích rozích. Pokud mřížku tvoří prostorově centrované buňky, obsahují navíc jednu částici uprostřed. Plošně centrovaná buňka má navíc částici ve středu každé své stěny. Nejlépe je to vidět na krychlové mřížce:
- prostá
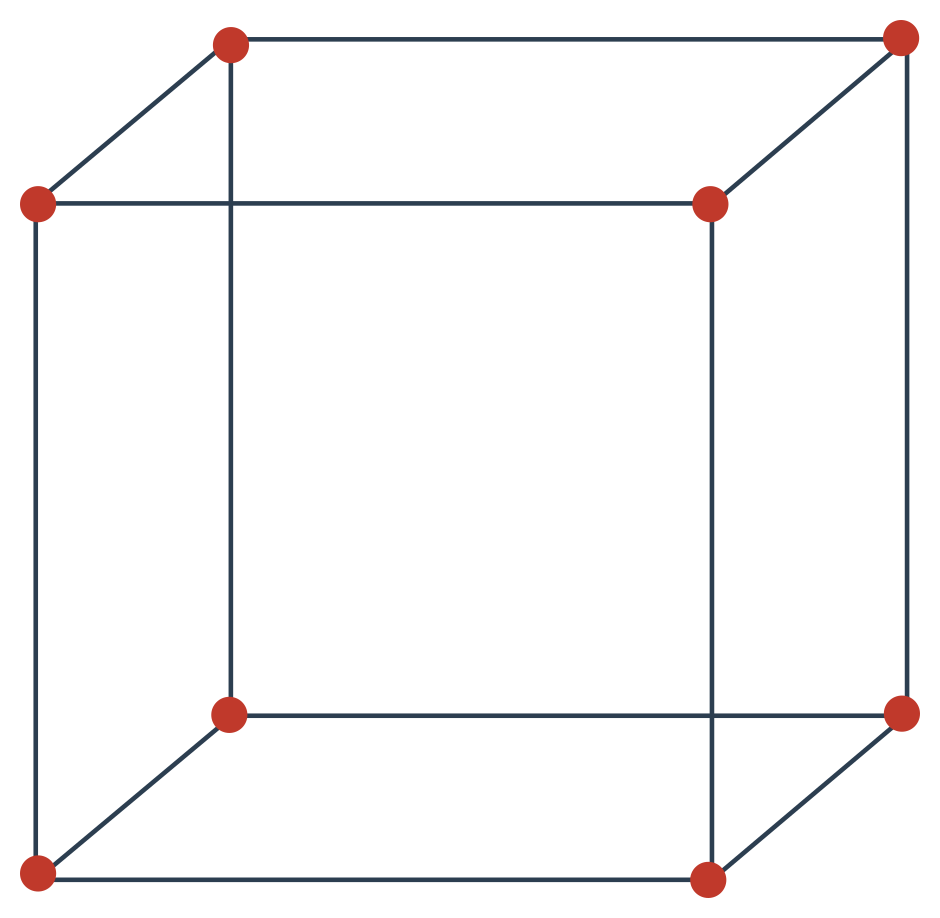
- prostorově centrovaná
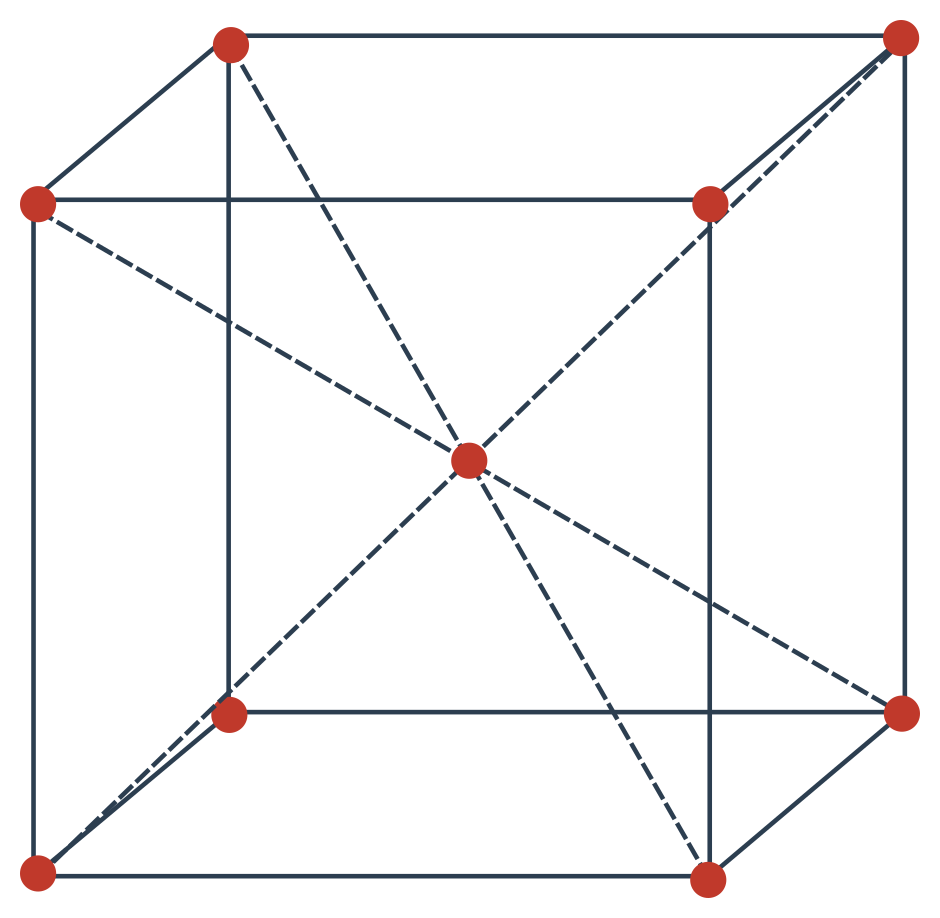
- plošně centrovaná
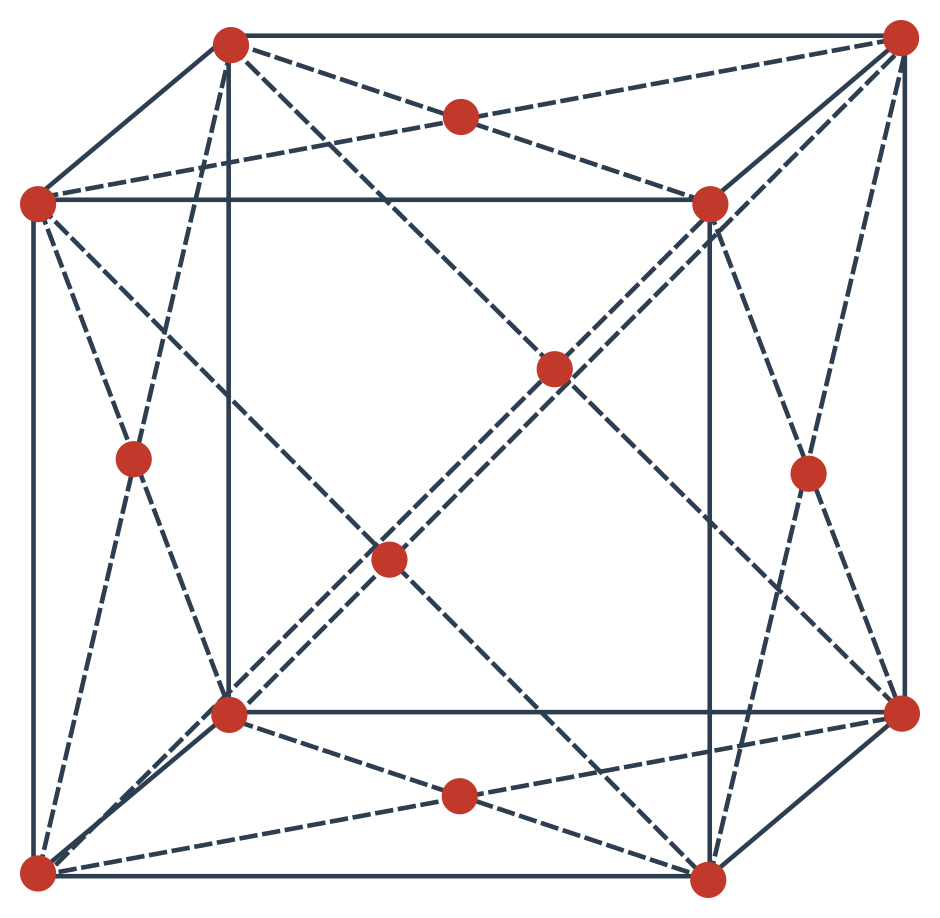
Počet částic připadající na jednu buňku
- Můžeme spočítat počet částic připadající na jednu buňku.
- Prostá: Každou částici sdíli osm buněk, jedna buňka se skládá z osmi částic, potom: \frac{1}{8}\cdot 8 = 1. Na jednu prostou buňku připadá jedna částice.
- Prostorově centrovaná: Stejné jako u prosté buňky plus jedna částice uvnitř, která celá připadá této buňce, proto: \frac{1}{8}\cdot 8 + 1 = 2. Na jednu prostorově centrovanou buňku připadají dvě částice.
- Plošně centrovaná: Stejné jako u prosté buňky plus šest částic ve stěnách, z nichž každá připadá dvěma buňkám, proto: \frac{1}{8}\cdot 8 + \frac{1}{2}\cdot 6 = 4. Na jednu plošně centrovanou buňku připadají čtyři částice.
Mřížkový parametr
Udává základní rozměr buňky. Většinou je to velikost hrany krychle/kvádru. Rozměrově bývá v jednotkách Ångstromů.
Hustota látky
- ze znalosti mřížkového parametru a typu buňky lze spočítat hustotu látky
- hustota je dána \varrho = \frac{m}{V}
- hmotnost spočítáme jako m = N\cdot m_i (N – počet částic na jednu buňku, m_i – hmotnost jedné částice)
- objem V = a^3 (objem krychle)
- výsledná hustota \varrho = \frac{N\cdot m_i}{a^3}.
Ångstrom?
V atomární fyzice i v dalších partiích se můžete setkat se zvláštními jednotkami označovanými A s kroužkem: Å. Metry jsou pro tento způsob využití příliš velké. Základní převodním vztahem je: 1 nm = 10 Å
NahoruTeplotní roztažnost: vzorce
Změny teplot ovlivňují rozměry a objem těles. To může být docela důležité, pokud například nechceme, aby rozpínající se most roztrhal silnici. Naštěstí to umíme počítat pomocí vzorců délkové nebo objemové roztažnosti.
Délková roztažnost
Platí pro každý rozměr, ale nejdůležitější pro tělesa, u nichž jeden rozměr výrazně převažuje nad zbývajícími dvěma (drát, koleje, mosty, apod.). Určuje změnu rozměru závislou na počáteční délce a změně teploty:
l = l_0\left[1+\alpha (t-t_0)\right]
- l_0 – (počáteční) délka při teplotě t_0
- l – délka při teplotě t
- \alpha – teplotní součinitel délkové roztažnosti (závisí na materiálu)
Pokud označíme rozdíl teplot t-t_0 jako \Delta t, můžeme psát:
l = l_0\left(1+\alpha \Delta t\right)
Výslednou délku l můžeme rozdělit na l_0 a prodloužení \Delta l, tedy l = l_0 + \Delta l. Pak platí:
\Delta l = l_0 \alpha (t-t_0).
Teplotní součinitel délkové roztažnosti \alpha
- Konstanta materiálu.
- Udává, o kolik se prodlouží těleso o délce 1 m při ohřátí/ochlazení o 1 ˚C (1 K).
- Jednotka je K^{-1}, příp. ^\circC^{-1}.
- Hodnota je \ll 1.
Příklad: Prodloužení měděného drátu
- Teplotní součinitel roztažnosti mědi je 0,000 017 K^{-1} (°C^{-1} ).
- Drát má délku 50 metrů
- O kolik se prodlouží při rozdílu teplot 10 °C?
- K výpočtu využijeme vzorec \Delta l = l_0 \alpha \Delta t
- Dosadíme zadané hodnoty \Delta l = 50\cdot 0,000 017\cdot 10\, \mathrm{m} = 5 \cdot 0,0017 \,\mathrm{m} = 0,0085 \,\mathrm{m} = 8,5 \,\mathrm{mm}
Proč má být \alpha \ll 1
- Co by se stalo, kdyby \alpha = 2?
- Představme si drát o délce 100 metrů.
- O kolik by se prodloužil při ohřátí o 10 °C (K)?
- K výpočtu využijeme vzorec \Delta l = l_0 \alpha \Delta t.
- Dosadíme zadané hodnoty \Delta l = 100\cdot 2\cdot 10\,\mathrm{m} = 2000\,\mathrm{m}.
- Drát by se prodloužil ze 100 metrů na 2 kilometry jen při ohřátí o 10 °C (K)!
Jiné teplotní stupnice
S teplotami se můžeme setkat jak ve stupních Celsia t, tak v kelvinech T (výjimečně ve stupních Fahrenheita \tau). Platí:
\Delta t = \Delta T
\Delta t = \frac{5}{9}\Delta \tau
Objemová roztažnost
Udává, jak se při změně teploty mění objem. Je tedy relevantní i pro kapaliny, pro které není důležitá délková roztažnost.
V = V_0\left[1+\beta (t-t_0)\right] = V_0\left(1+\beta \Delta t\right)
- V_0 – objem při teplotě t_0
- V – objem při teplotě t
- \beta – teplotní součinitel objemové roztažnosti (závisí na materiálu)
Teplotní součinitel objemové roztažnosti \beta
- Konstanta materiálu.
- Udává, o kolik se změní objem tělesa o objemu 1 m^3 při ohřátí/ochlazení o 1 ˚C (1 K).
- Jednotka je opět K^{-1}, příp. ^\circC^{-1}.
- Hodnota \ll 1.
- Přibližně platí \beta \approx 3\alpha.
Délková vs. objemová roztažnost
- Na obrázku máme dvě tělesa o stejném objemu, ale různých rozměrech, bude jejich teplotní délková/objemová roztažnost stejná?
- Délková roztažnost:
Změna výšky prvního tělesa \Delta l_1 = a\alpha\Delta T
Změna výšky druhého tělesa: \Delta l_2 = 2a\alpha\Delta T - Objemová roztažnost
Změna objemu prvního tělesa: \Delta V_1 = V_0\beta\Delta T
Změna objemu druhého tělesa: \Delta V_2 = V_0\beta\Delta T - Změny rozměrů se liší, ale změny objemů jsou stejné.
Hustota a objemová roztažnost
Protože se hmotnost tělesa typicky nemění, dá se odvodit z V=V_0\left(1+\beta \Delta t\right) i přibližný vzorec pro hustotu:
\rho=\rho_0\left(1-\beta \Delta t\right)
Takže když objem vzroste, hustota klesá.
NahoruVzájemné působení magnetů
Magnety na sebe mohou působit magnetickými silami. Ty (podobně jako elektrické síly) mohou být přitažlivé i odpudivé.
Magnet má vždy dva magnetické póly severní a jižní (i kdybychom magnet rozpůlili, budou oba úlomky magnety mít dva póly). Česky se póly označují jako S a J, anglicky jako N a S (north a south). Severní pól může být označen barevně (červeně).
Opačné póly se přitahují a souhlasné póly se odpuzují a to tím víc, čím blíž jsou u sebe.
K magnetům se přitahují železné věci. Používají se tedy například u modernějších kuchyňských dvířek, ve chňapkách na vaření aj. Dále je najdeme třeba v klasických HDD nebo magnetických tabulích. Přírodním magnetem je hornina magnetovec, uměle je vyrábíme například z neodymu, nebo feritů.
NahoruPůsobení magnetů na látky
Látky kolem nás můžeme dělit podle toho, jak reagují na blízkost trvalého magnetu.
- nemagnetické – vůbec na magnet nereagují
- magnetické – těleso se začne přitahovat k magnetu
Nemagnetické jsou všechny kapaliny, všechny plyny a většina pevných látek (např. guma, plast, dřevo). Magnetickými látkami se běžně myslí tzv. feromagnetické materiály. Je jich jen málo, zejména jde o některé kovy (např. železo, ocel), ale zdaleka ne všechny (třeba měď nebo hliník magnetické nejsou).
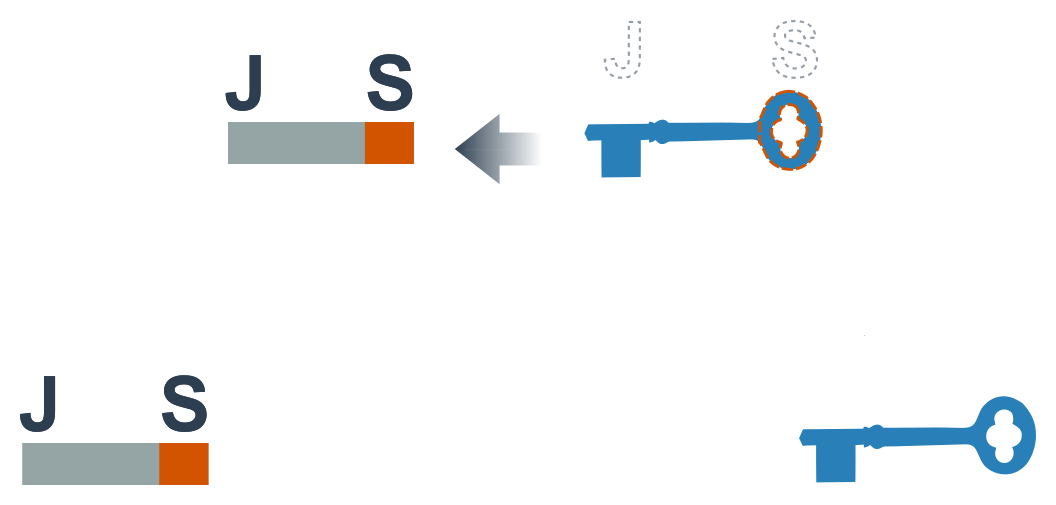
Na rozdíl od dvou magnetů se těleso z feromagnetického materiálu k magnetu vždy přitahuje. Vlastně se tedy samy stávají magnety, ale jen dočasně – dokud jsou poblíž trvalého magnetu.
Zajímavosti
Ve skutečnosti magnetické pole alespoň trošku působí na každý materiál, ale u většiny materiálů tak nepatrně, že jej zanedbáváme a považujeme je právě za nemagnetické. Tyto slabé typy působení se nazývají diamagnetismus (slabounké odpuzování, například bizmut) a paramagnetismus (slabé přitahování, například kyslík).


