Pravidla pro počítání celkové kapacity více kondenzátorů (respektive kapacit obecně) jsou velmi podobná jako ta pro rezistory. Akorát přesně naopak.
Paralelní zapojení
Pro paralelní kondenzátory platí podobný vzorec jako pro sérii rezistorů (tedy prostý součet):
C_{12}=C_1+C_2
Případně pro více paralelně zapojených kondenzátorů je celková C rovna C=C_1+C_2+C_3+\cdots
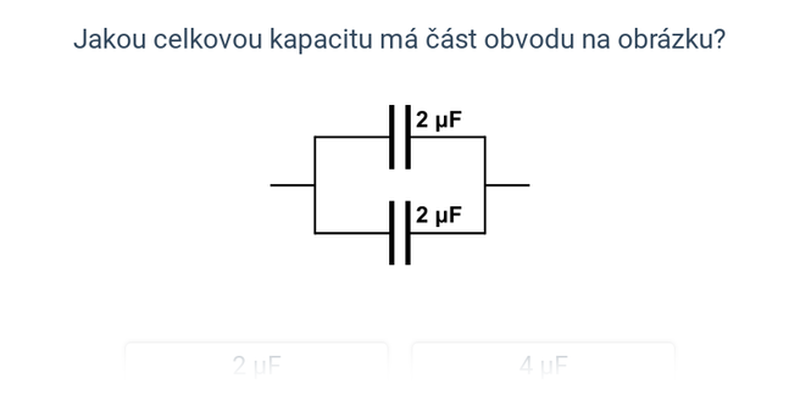
Příklad: Dva stejné kondenzátory paralelně
Jakou kapacitu mají dva paralelně zapojené kondenzátory s kapacitou C?
- Celková kapacita je součet jednotlivých kapacit.
- C_{12} je tedy C plus C
- Odpověď je tedy 2\cdot C.
Příklad:Tři konkrétní kondenzátory paralelně
Jakou celkovou kapacitu mají paralelně zapojené kondenzátory 10 nF, 5 nF a 100 nF?
- Celková kapacita je součet jednotlivých kapacit.
- C_{123} je tedy 10 nF plus 8 nF plus 100 nF
- Odpověď je tedy 118 nF.
Sériové zapojení
Pro sériové zapojení kondenzátorů platí podobný vzorec jako pro paralelní rezistory. tedy \frac{1}{C_{12}}=\frac{1}{C_{1}}+\frac{1}{C_{2}} což můžeme upravit na
C_{12}=\frac{C_{1} C_{2}}{C_{1}+C_{2}}
Pro více sériově zapojených kondenzátorů splňuje celková C rovnici \frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}+\cdots (ze které si musíme C vyjádřit).
Příklad: Dva stejné kondenzátory sériově
Jakou kapacitu mají dva sériově zapojené kondenzátory s kapacitou C?
- Použijeme C_{12}=\frac{C_{1} C_{2}}{C_{1}+C_{2}}
- Po dosazení C_{12}=\frac{C\cdot C}{C+C}=\frac{C^2}{2C}=\frac{C}{2}.
- Odpověď je tedy \frac{C}{2}.
Příklad: Dva konkrétní kondenzátory sériově
Jakou celkovou kapacitu mají sériově zapojené kondenzátory 1 pF a 3 pF?
- Použijeme C_{12}=\frac{C_{1} C_{2}}{C_{1}+C_{2}}
- Po dosazení C_{12}=\frac{1\cdot 3}{1+3}\,\mathrm {pF}=\frac{3}{4}\,\mathrm {pF}.
- Odpověď je tedy 3/4 pF.
Složitější zapojení
Zjednodušujeme opět od nejmenších celků, stejně jako rezistory.
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.