Pomocí Bernoulliho rovnice (\frac{1}{2}\rho v_1^2+p_1 = \frac{1}{2}\rho v_2^2+p_2) můžeme odvodit rychlost tryskání vody z (malého) otvoru v nějaké nádobě.

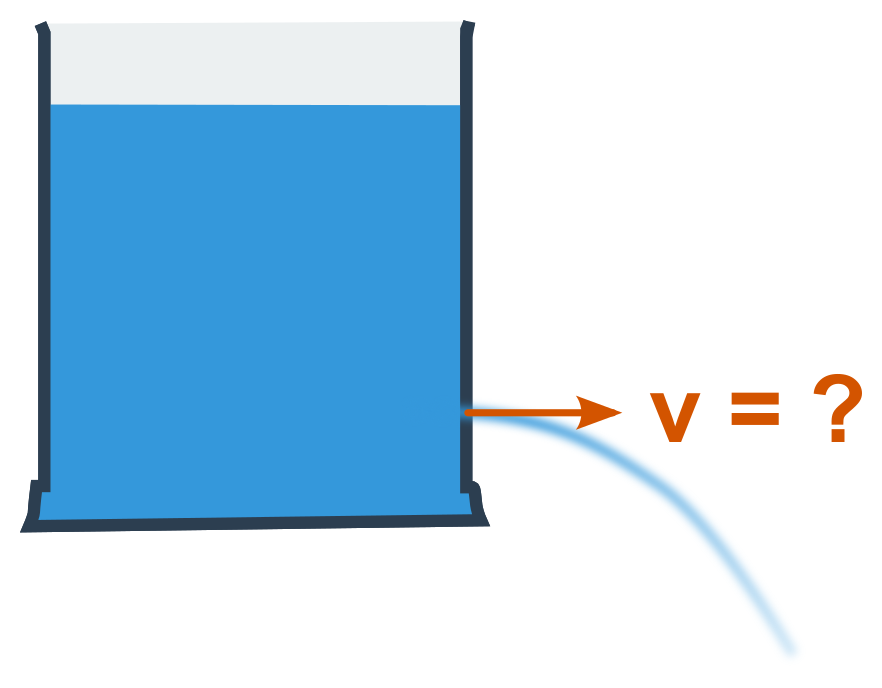
Zevnitř (index 1) je rychlost prakticky nulová a vně (index 2) je zase nulový tlak (pokud od obou stran odečteme atmosférický tlak). Po dosazení těchto nul do rovnice výše dostaneme p_1 = \frac{1}{2}\rho v_2^2.

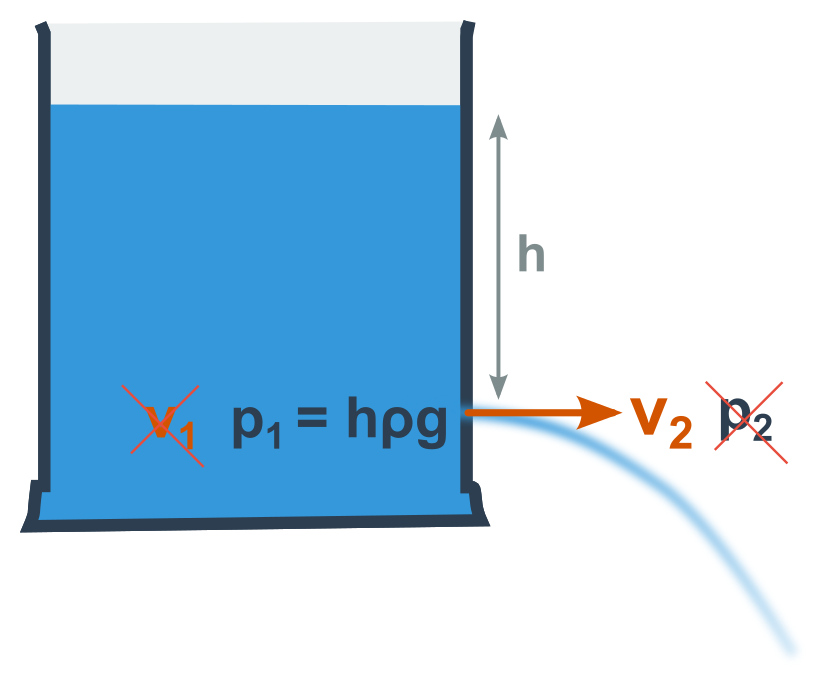
Tlak p_1 je vlastně hydrostatický tlak v nádobě (h\rho g) a rychlost zůstala jen jedna, nemusíme ji tedy indexovat. Máme h\rho g=\frac{1}{2}\rho v^2, z čehož vyjádříme rychlost:

v = \sqrt{2 h g}