Bernoulliho rovnice popisuje souvislost mezi tlakem p v kapalině (o hustotě \rho) a rychlostí jejího proudění v. Podél jedné proudnice platí:
\frac{1}{2}\rho v^2+p = \mathrm{konst.}
Příklad: Zužující se trubice
Rychlost se v užší části trubice zvedla na dvojnásobek. Jak se tam změní tlak kapaliny?
- Protože se zvedla rychlost v, zvedla se i hodnota \frac{1}{2}\rho v^2 (\rho je u kapalin konstantní).
- Podle Bernoulliho rovnice má ale být \frac{1}{2}\rho v^2+p stále stejné. Musí tedy klesnout druhá část součtu – p.
- Odpověď tedy zní, že tlak klesne.
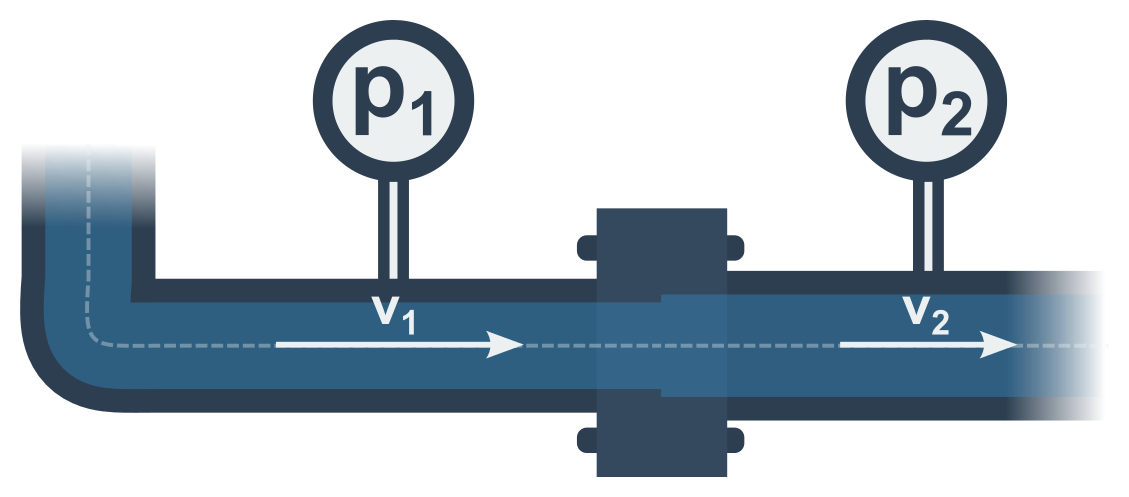
Pro dvě místa na téže proudnici tedy platí (pro konstantní hustotu):
\frac{1}{2}\rho v_1^2+p_1 = \frac{1}{2}\rho v_2^2+p_2
Příklad: Rychlost proudění podle změny tlaků
Voda proudí potrubím 1 m/s a má v něm tlak 5000 Pa. Jaký je tlak v části, kde voda proudí rychlostí 2 m/s?
- Platí \frac{1}{2}\rho v_1^2+p_1 = \frac{1}{2}\rho v_2^2+p_2.
- Známe všechno (voda má \rho=1000\,\mathrm{kg/m^3}) kromě p_2. To je naše neznámá, kterou musíme vyjádřit.
- Tlak p_2 osamostatníme odečtením \frac{1}{2}\rho v_2^2 od obou stran rovnice.
- Dostaneme: p_2=\frac{1}{2}\rho v_1^2+p_1-\frac{1}{2}\rho v_2^2
- Dosadíme: p_2=\frac{1}{2}1000\cdot 1^2+5000-\frac{1}{2}1000\cdot 2^2\,\mathrm{Pa}=500\cdot 1+5000-500\cdot 4\,\mathrm{Pa}=3500\,\mathrm{Pa}
- Tlak tedy klesne na 3500 Pa.
Pro jednoduchost obvykle definujeme Bernoulliho rovnici pro vodorovnou uzavřenou trubku.
Jak by to bylo pro nevodorovnou trubku?
Pro nevodorovnou trubku bychom museli do rovnice započítávat i hydrostatický tlak p_h.
Bernoulliho rovnice vlastně říká, že zvýšením rychlosti proudění poklesne tlak. Tento princip platí i pro libovolné neturbulentní proudění kapaliny nebo plynu. Matematický vzorec sice v takovém případě neplatí přesně, ale jako odhad se hodí.
Tohoto principu se využívá v řadě případů, kde chceme vůči okolnímu prostředí vytvořit podtlak (fixírka, některé typy vývěv, profil křídla letadel).
Zajímavosti
Bernoulliho rovnice je vlastně rovnice zachování energie na jednotku objemu. Po vynásobení objemem je to ještě patrnější – získáte \frac{1}{2}m v^2 (kinetická energie) a p\cdot V=p\cdot S\cdot s=F\cdot s (práce/potenciální energie).
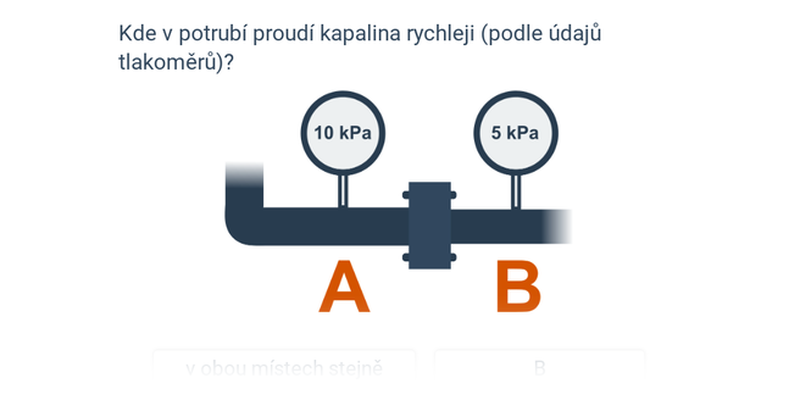
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.