Skládání sil

Skládání, neboli sčítání sil je nejčastěji potřeba, když zjišťujeme výslednou sílu působící na těleso. Protože síla je vektorová veličina, skládání sil je vlastně sčítáním vektorů. Proto následující odstavce platí i pro jakoukoliv jinou vektorovou veličinu (např. hybnost, moment síly, …).

U sčítání více sil (F_1, F_2, F_3, …) často výslednou sílu označujeme bez indexu (F), v příkladech níže ji ale pro jednoznačnost označíme indexem „celk“.

Síly ležící v jedné přímce

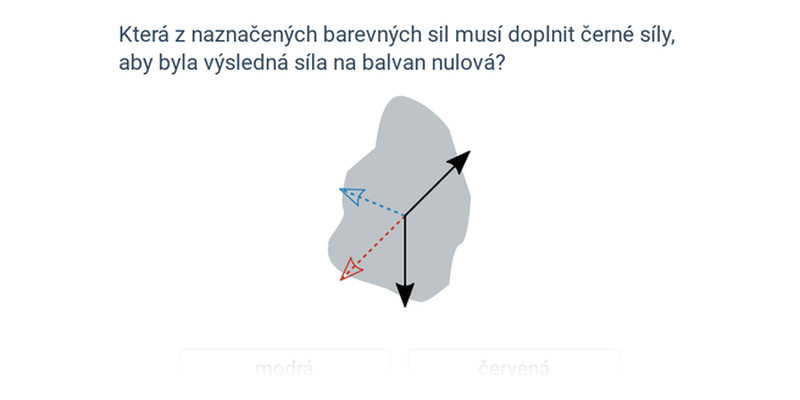
Nejjednodušší je, když leží všechny síly v jedné přímce (např. všechny míří vodorovně doprava nebo doleva):

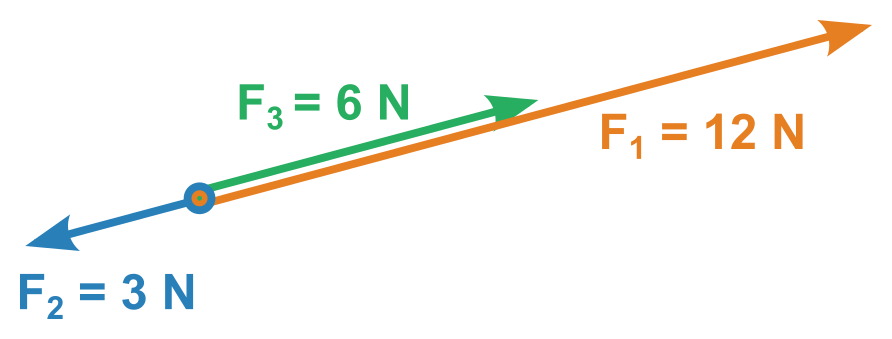
1. Zvolíme směr (jeden z těch dvou).

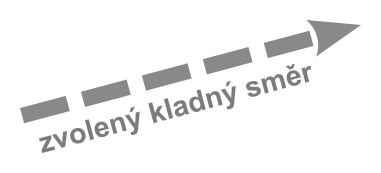
2. Přičítáme velikosti sil mířících zvoleným směrem, a odečítáme ty opačné.

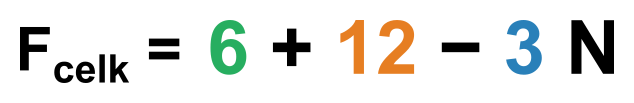
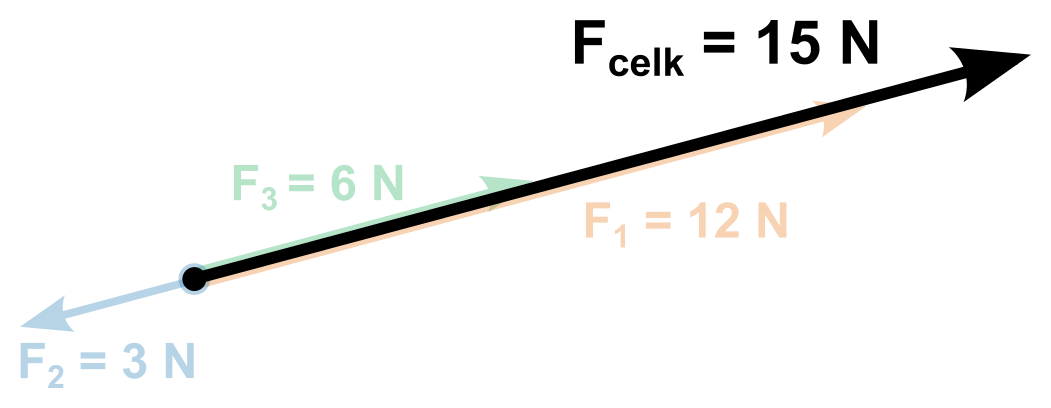
3. Vyjde nám velikost (délka) výslednice. Pokud je kladná, míří námi zvoleným směrem, pokud ne, míří na druhou stranu.

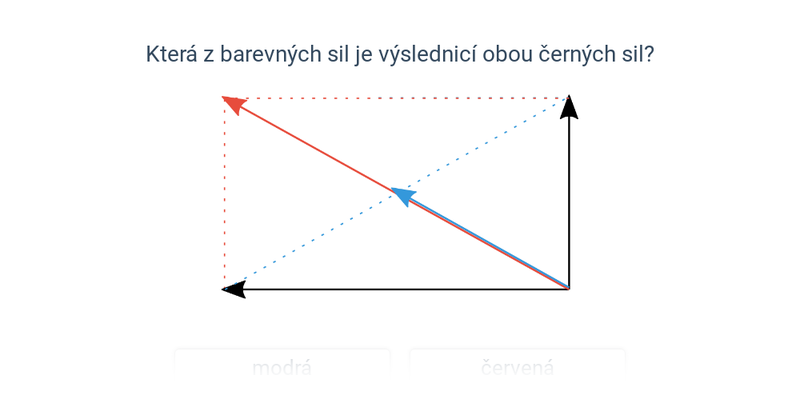
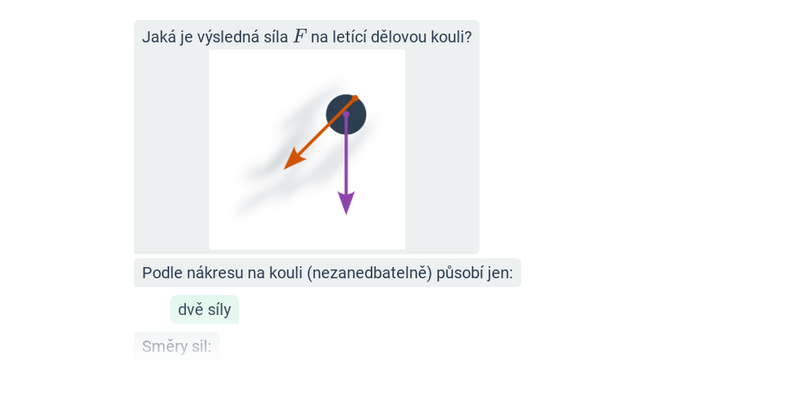
Dvě síly neležící v jedné přímce (grafické řešení)

1. Síly narýsujeme tak, aby vycházely z jednoho bodu/působiště

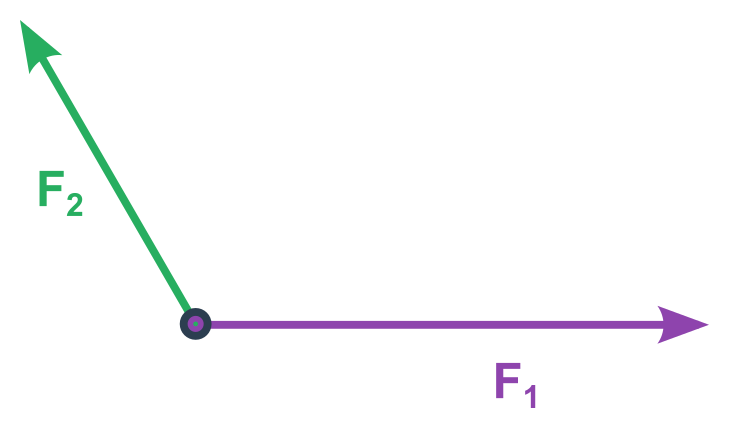
2. Doplníme na rovnoběžník. Výsledkem je jeho úhlopříčka vycházející ze společného počátku sil

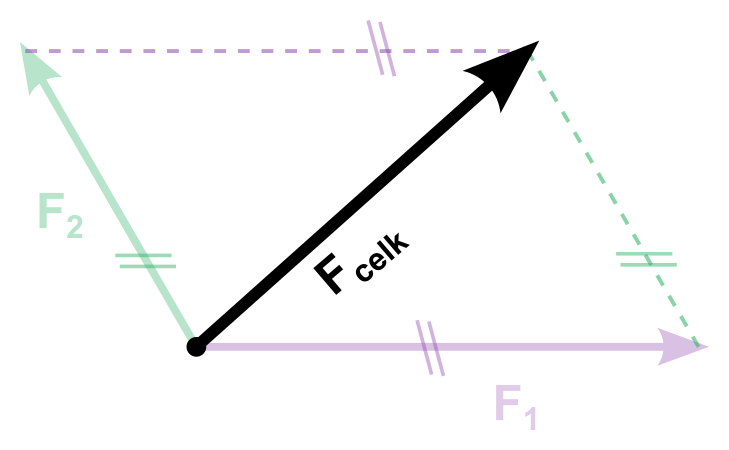
Pokud jsou na sebe síly kolmé, jde o úhlopříčku obdélníka s délkou podle Pythagorovy věty F=\sqrt{F_1^2+F_2^2}.

Více sil neležících v jedné přímce (grafické řešení)

1. Vektory narýsujeme tak, aby vycházely z jednoho bodu/působiště

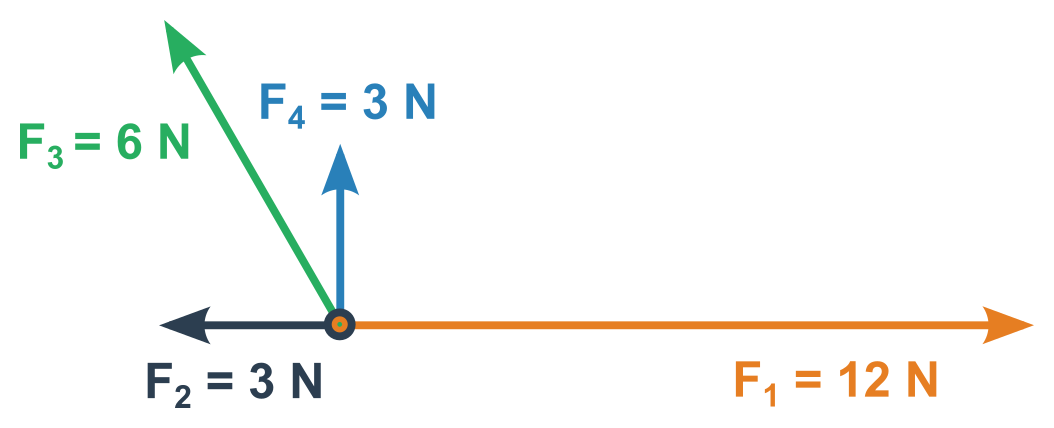
2. Doplňováním na rovnoběžník sčítáme postupně jednotlivé vektory dokud nezbyde jeden výsledný vektor (pořadí je na nás, nejjednodušší je ale sdružovat rovnoběžné síly a následně ty na sebe kolmé)

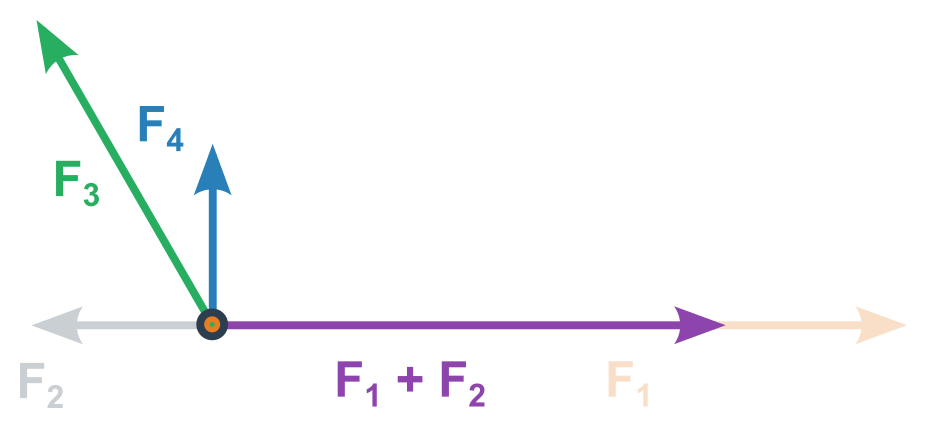
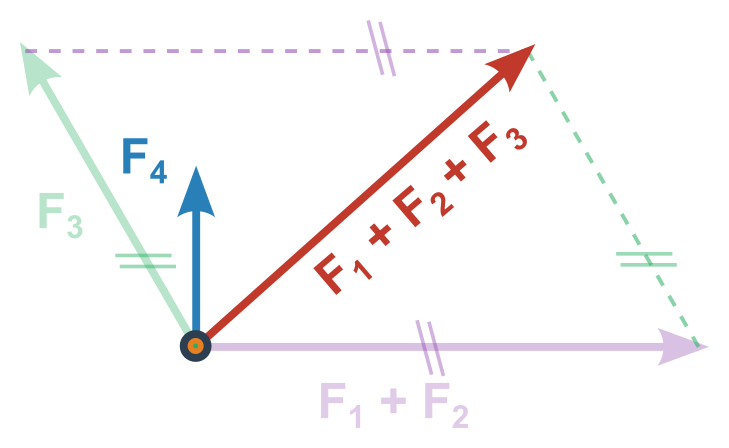
Souřadnicové řešení

1. Musíme zvolit nějakou kartézskou soustavu souřadnic, například ve směru jedné ze sčítaných sil.

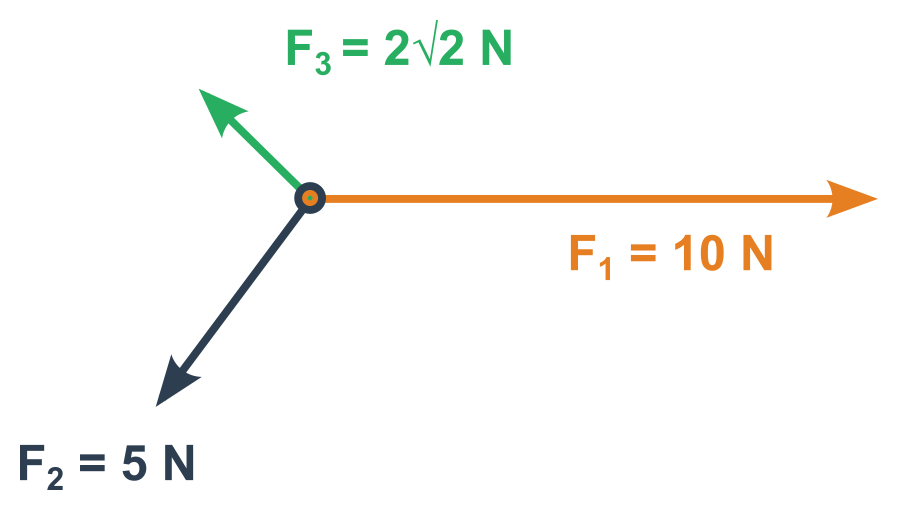
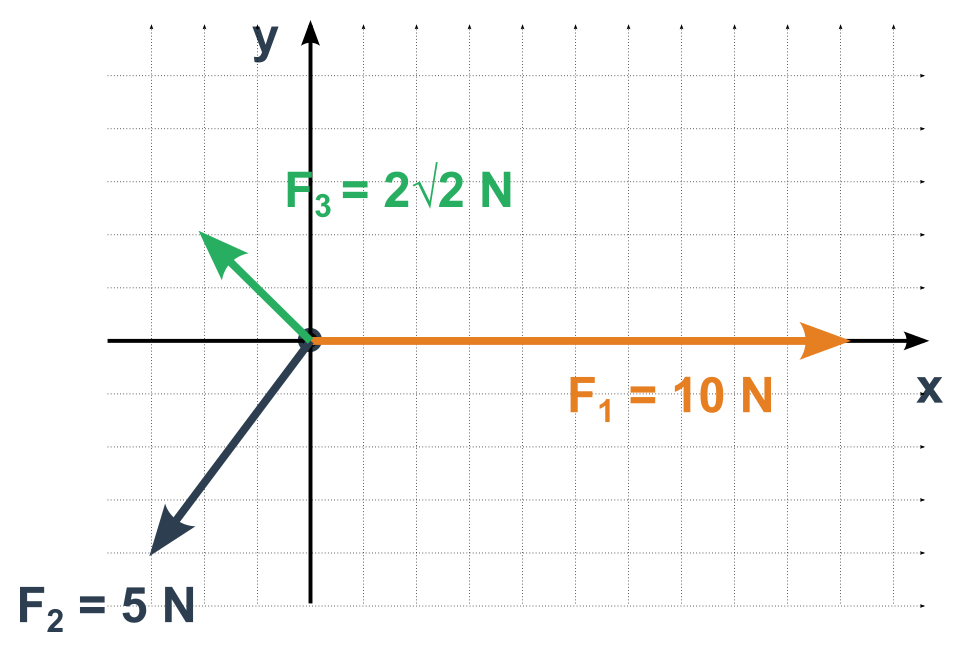
2. Určíme jednotlivé složky všech vektorů sil v této soustavě

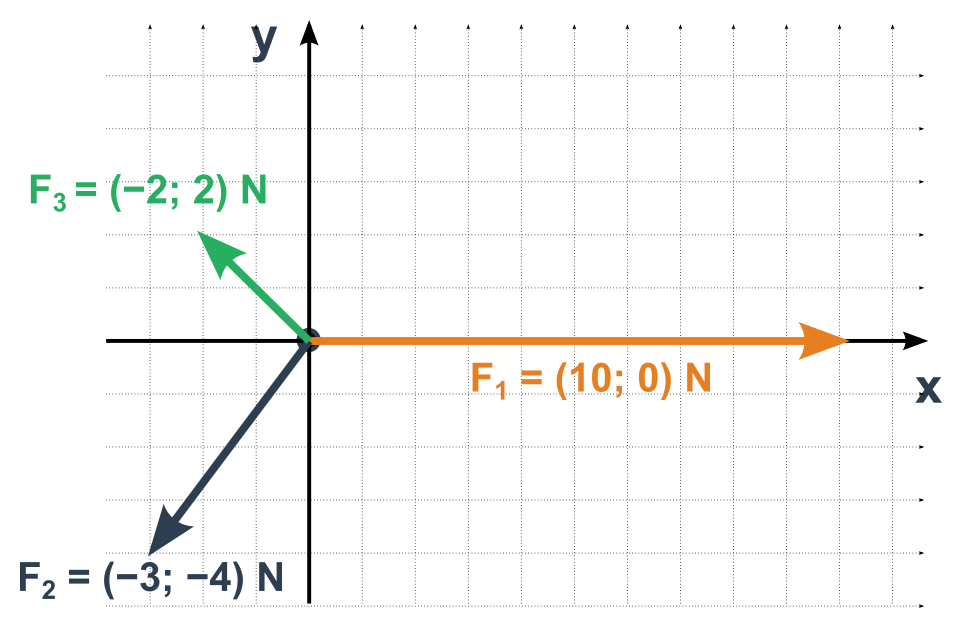
3. Sečteme zvlášť stejné složky všech sil

4. Výsledkem je vektor výsledné síly o souřadnicích které nám vyšly

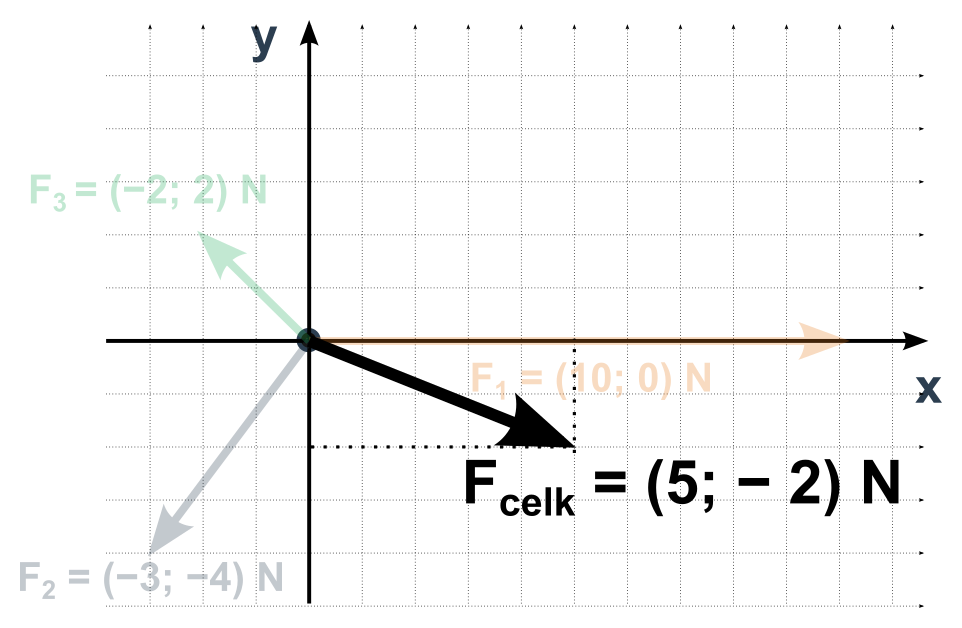
Velikost je podle Pythagorovy věty odmocnina z druhých mocnin souřadnic (zde odmocnina z 5^2+(−2)^2, tedy \sqrt{29}).

Tipy

• Pokud jsou na sebe dvě síly kolmé, určíme délku výsledné síly i se znalostí úhlopříček obdélníka (Pythagorova věta, F_\mathrm{celk}=\sqrt{F_1^2+F_2^2})

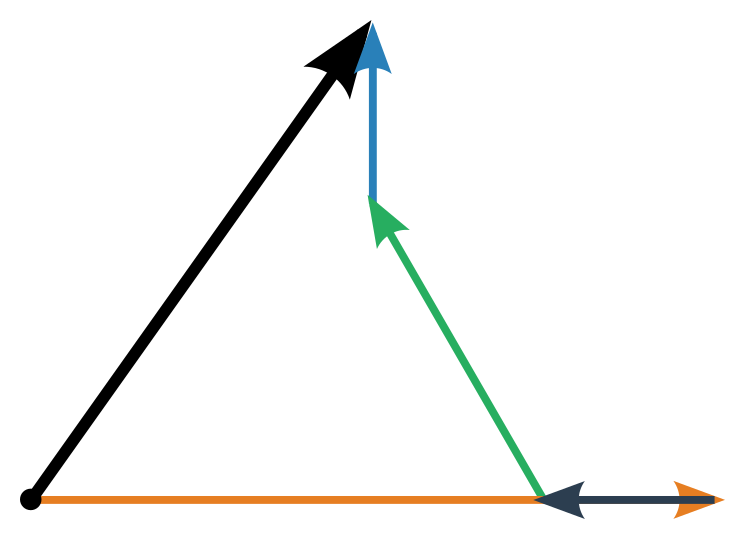
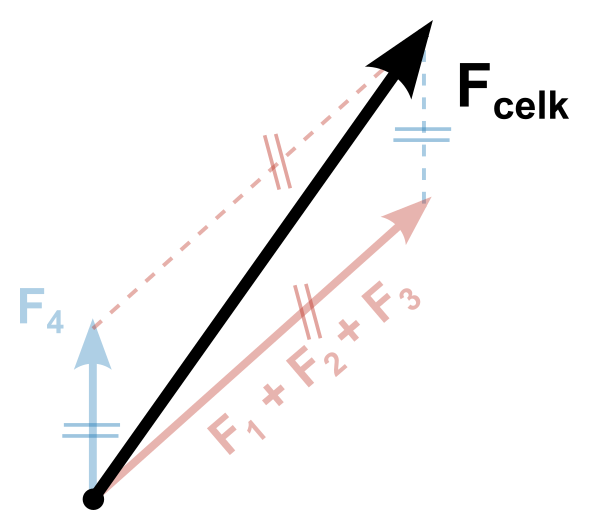
• Alternativně můžeme grafické skládání sil pojmout tak, že síly připojujeme jednu za druhou jako na řetěz (viz obrázek). Je to sice názornější, ale rýsovalo by se to mnohem hůř.