Dráha zrychleného pohybu

umime.to/WM2

Graf závislosti rychlosti na čase u rovnoměrného pohybu vypadá takto:

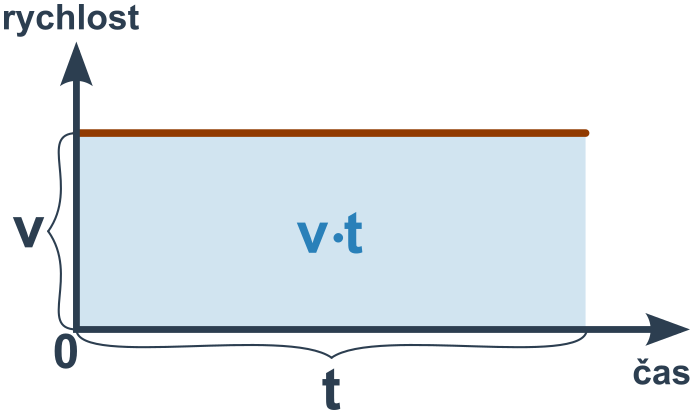
Plocha pod křivkou rychlosti má obsah v\cdot t (obsah obdélníka) což je přesně rovno dráze rovnoměrného pohybu. To platí obecně – obsah plochy pod křivkou rychlosti v grafu v/t je roven dráze.

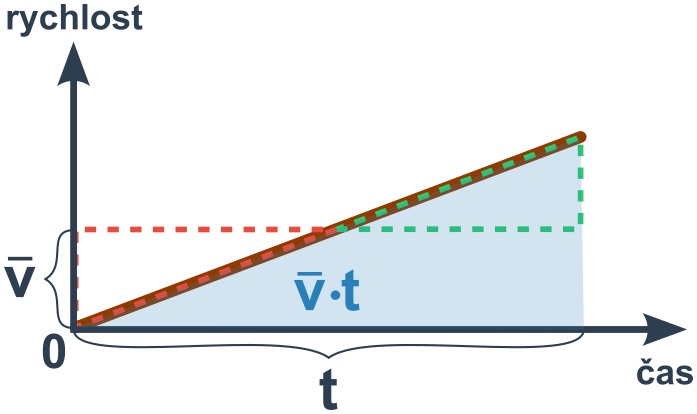
U rovnoměrně zrychleného pohybu (konstantní a) nejde o obdélník, plocha je ale stejná jako plocha obdélníka o výšce průměrné rychlosti \bar v (plocha △ a △ je totiž stejná).

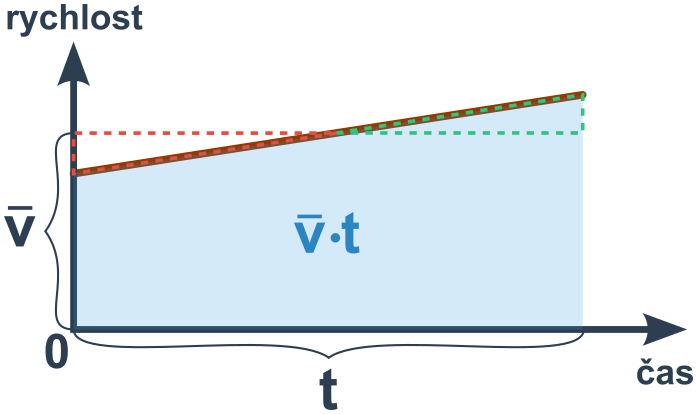
Dráhu rovnoměrně zrychleného pohybu počítáme v různých situacích:

Pohyb začíná z klidu

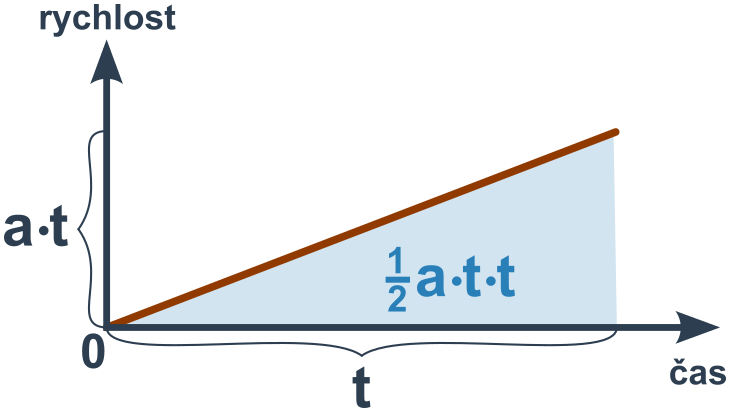
Pro rychlost platí v=a\cdot t (přímá úměra). Dráha (obsah pod křivkou) je rovna:

s=\frac{1}{2}at^2

Příklad: Dráha rozjíždějícího se auta

Auto se z klidu rozjíždí se zrychlením 2 m/s². Jakou dráhu ujede za 3 s?

Zrychlení a je 2 m/s² a čas t je 3 s.
Můžeme je přímo dosadit do s=\frac{1}{2}at^2.
s=\frac{1}{2}at^2=\frac{1}{2}2\cdot 3^2\,\mathrm m=9\,\mathrm m
Auto urazilo 9 m.

Příklad: Dráha valícího se kamene (grafická úvaha)

Na svahu se uvolnil kámen a začal se kutálet dolů se zrychlením 0,5 m/s². Jakou dráhu urazí za 10 s?

Zrychlení a je 0,5 m/s² a čas t je 10 s.
V grafu v-t je první odvěsna △ (vodorovná) rovna t, tedy 10 s.

Druhá odvěsna je rovna a\cdot t, tedy 5 m/s– to je vlastně konečná rychlost v čase 10 s.
Obsah △ je polovina součinu odvěsen. Tedy s=\frac{1}{2}\cdot 10\cdot 5\,\mathrm m=25\,\mathrm m
Kámen tedy urazil 25 m.

Těleso se už pohybuje rychlostí v_0 a zrychluje

S nenulovou v_0 máme rychlost v=v_0+a\cdot t. Pak je dráha rovna součtu:

s=v_0\cdot t + \frac{1}{2}at^2

I to můžeme vyčíst z grafu (celková plocha = součet ▯ v_0\cdot t a △ \frac{1}{2}at^2):

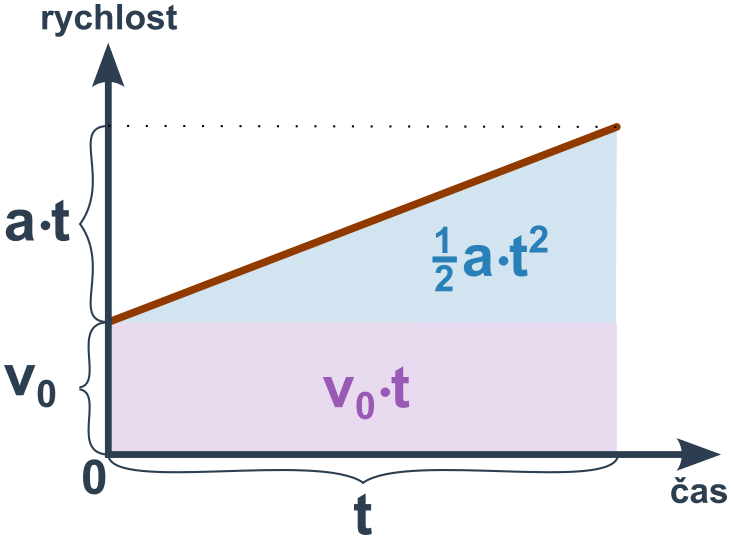
Příklad: Nástup závodníka do finiše

Závodník v cílové rovince z původní rychlosti 5 m/s rovnoměrně zrychloval (o 1 m/s²). Jak daleko byl cíl, pokud doběhl za 4 s?

Zrychlení a je 1 m/s², čas t je 4 s a rychlost v_0 je 5 m/s.
Můžeme je přímo dosadit do s=v_0\cdot t+\frac{1}{2}a t^2.
s=v_0\cdot t+\frac{1}{2}at^2=5\cdot 4 + \frac{1}{2}1\cdot 4^2\,\mathrm m=20+8\,\mathrm m=28\,\mathrm m
Když začal zrychlovat, byl závodník 28 m od cíle.

Těleso se už pohybuje rychlostí v_0 a zpomaluje

Platí totéž co v předchozím bodě, jen obsah △ odečítáme.

s=v_0\cdot t -\frac{1}{2}at^2

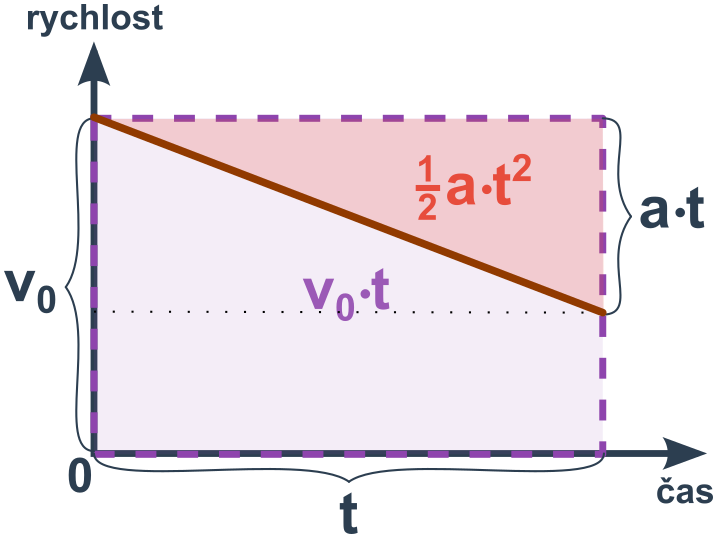
Příklad: Brzdění auta

Řidič plynule zpomaloval z 30 m/s po dobu 2 se zrychlením 5 m/s². Jakou dráhu urazil?

Čas t je 2 s, rychlost v_0 je 30 m/s a zrychlení a je 5 m/s².
Můžeme tedy přímo dosadit do s=v_0\cdot t-\frac{1}{2}a t^2.
s=v_0\cdot t-\frac{1}{2}at^2=30\cdot 2 - \frac{1}{2}5\cdot 2^2\,\mathrm m=60-10\,\mathrm m=50\,\mathrm m
Řidič během těch dvou sekund zpomalování urazil 50 m.