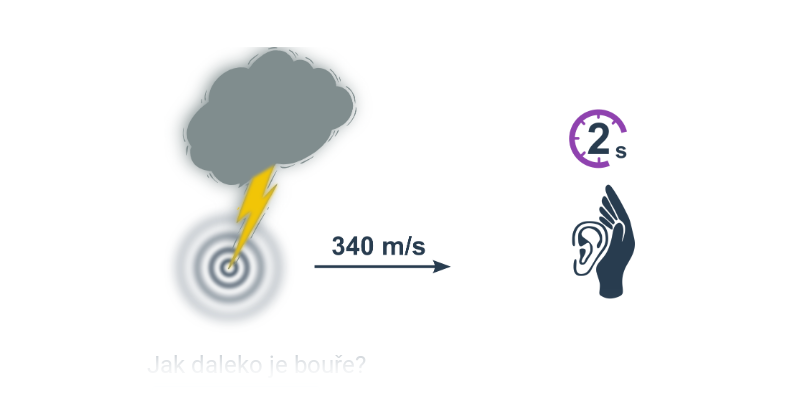
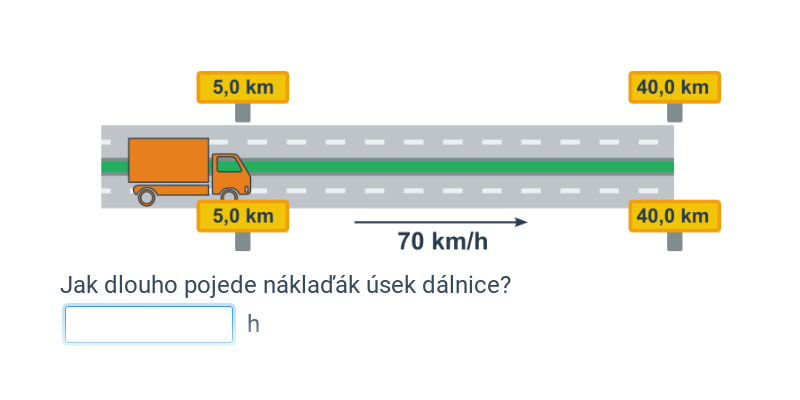
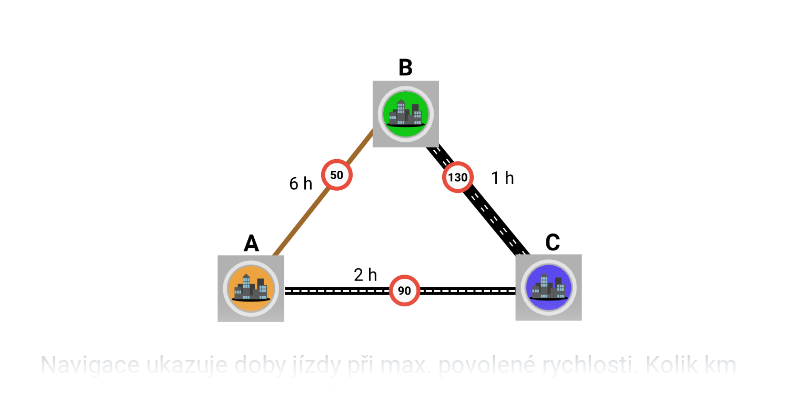
Rychlost, dráha, čas
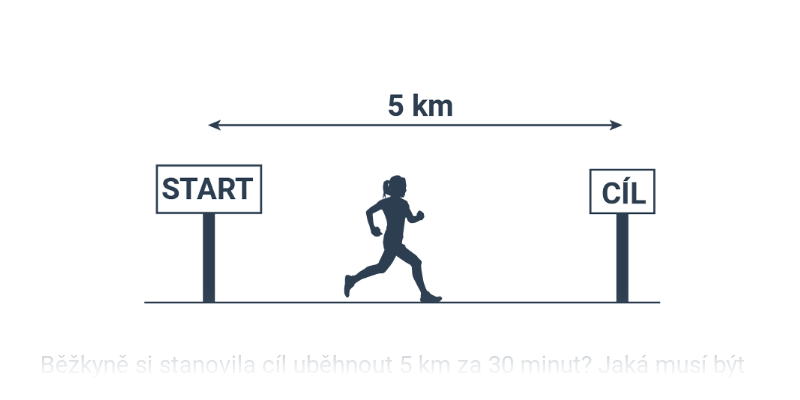
WEEVztah mezi rovnoměrnou (nebo alespoň průměrnou) rychlostí v drahou s a časem pohybu t popisují vzorce:
v=\frac{s}{t}
s=v\cdot t
t=\frac{s}{v}
V jednoduchých případech pouze určíme správný vzorec a dosadíme.
U mnoha pohybů těles ovšem před dosazením musíme udělat něco navíc, např. převést správně jednotky nebo určit s ze změny poloh.
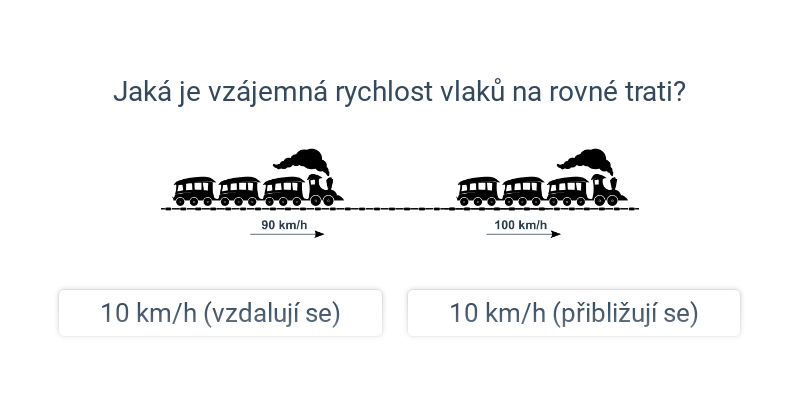
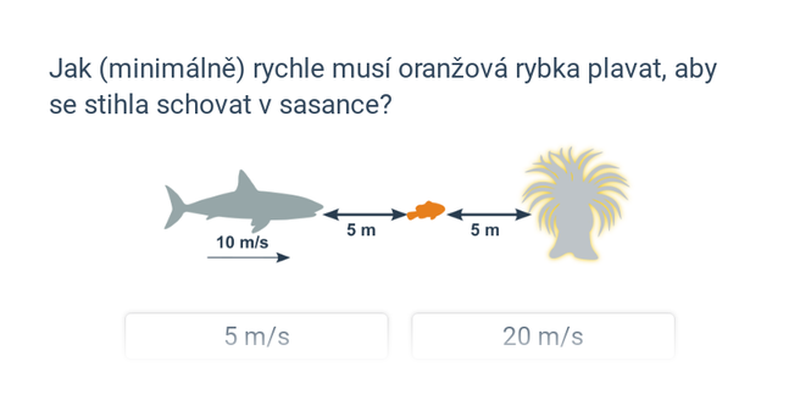
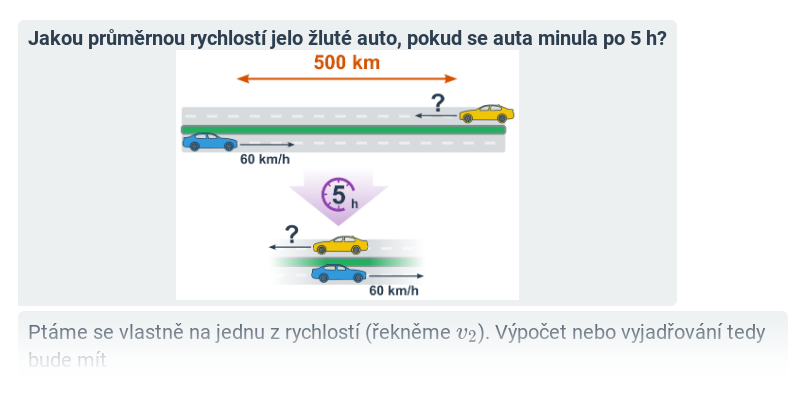
Konečně můžeme pomocí těchto vztahů také řešit vzájemný pohyb více těles.
Vztahový trojúhelník (pyramida)
Pokud známe nějaký vzorec typu \bf{A=B\cdot C} nebo \bf{A=B/C} (například v=s/t) můžeme pomocí jednoduché pomůcky zjistit, jak vypadají vzorce pro \bf{B} a pro \bf{C}.
- Nakreslíme si trojúhelníkovou pyramidu (zatím prázdnou).
- Zakreslíme do ní pravou stranu rovnice (naše s/t), tak aby vypadala graficky stejně jako ve vzorci (dělení jako zlomek nad sebou, případně násobení vedle sebe v dolním patře).
- Na zbývající místo doplníme levou stranu vzorce.

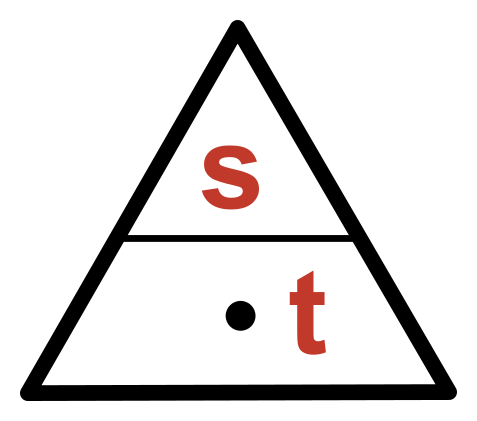
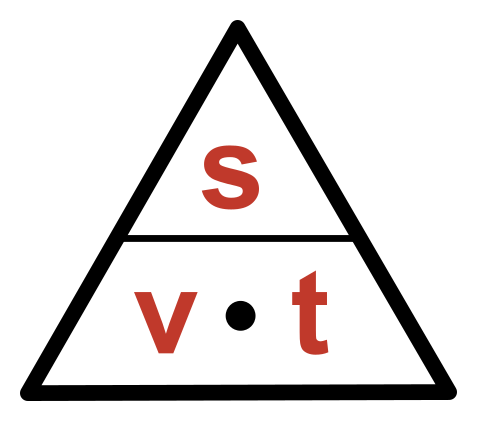
- Nyní stačí pro výpočet jakékoliv veličiny zakrýt tuto veličinu prstem a podívat se jak vypadají ostatní nezakryté.
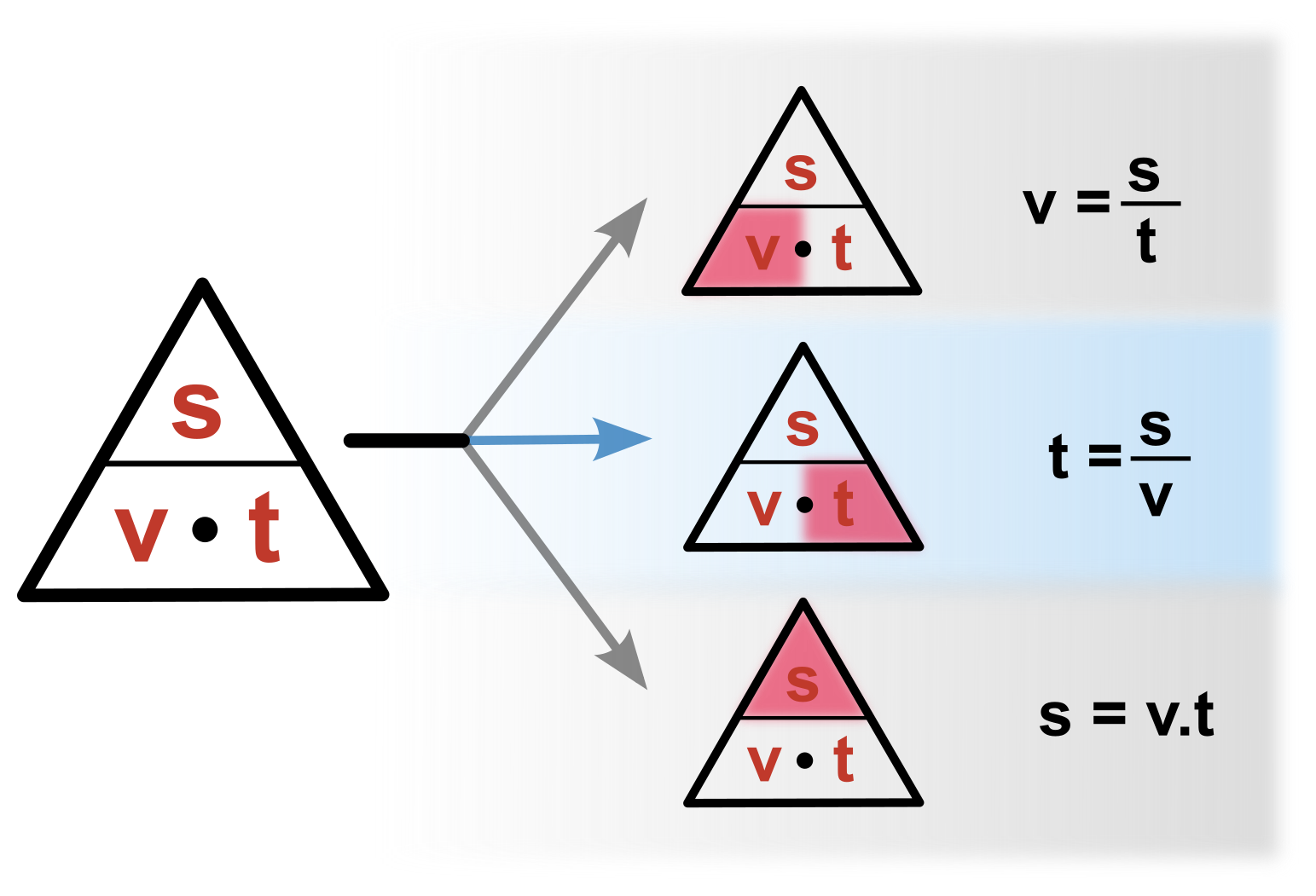
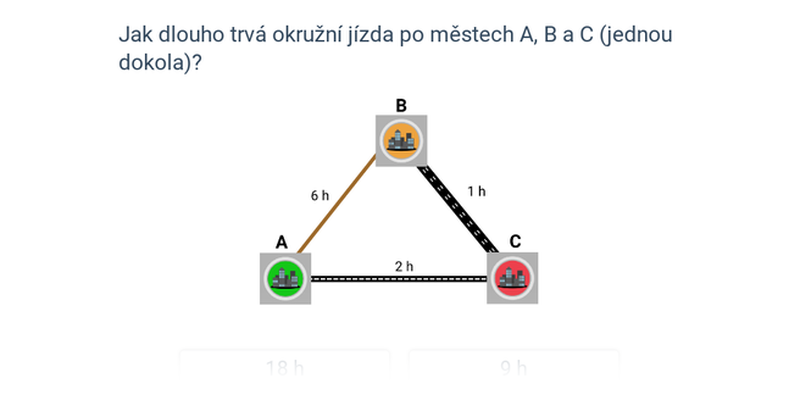
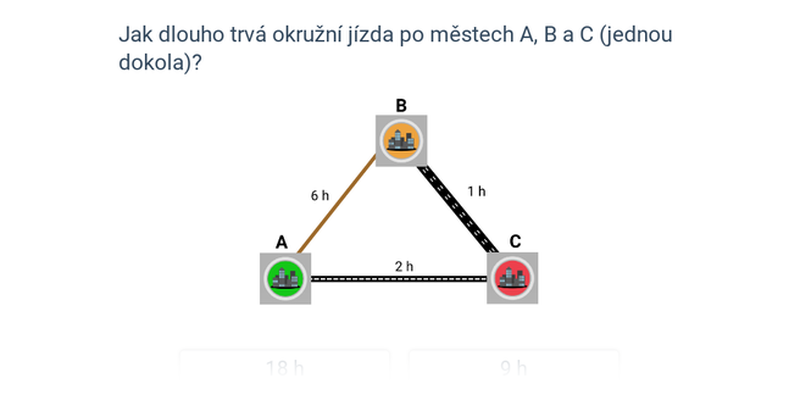
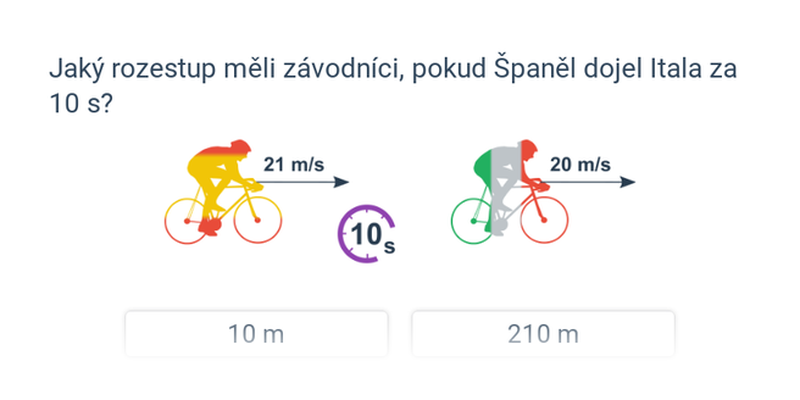
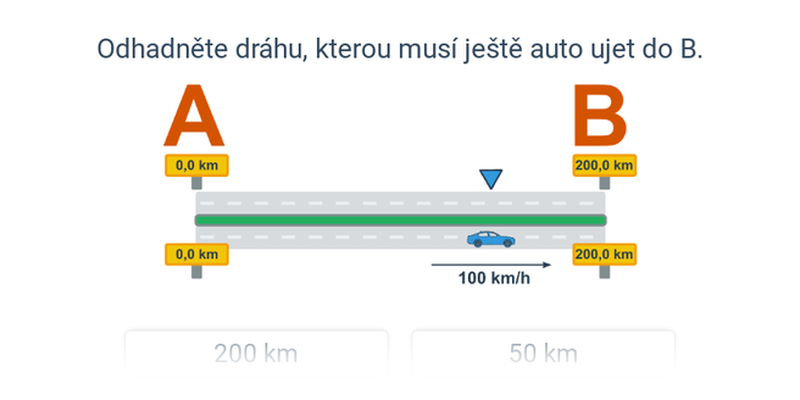
Rozhodovačka
Rychlé procvičování výběrem ze dvou možností.
Krok po kroku
Doplňování jednotlivých kroků v rozsáhlejším postupu.
Vpisování
Cvičení, ve kterém píšete odpověď na klávesnici.