
Spojování rezistorů

Rezistory jsou součástky, jejichž úkolem je klást elektřině odpor. Samy jsou někdy nepřesně označované jako „odpory“. Odbor je hlavní vlastnost rezistorů, ale mají ji i jiné součástky. Elektrická energie se v nich přeměňuje na teplo.
Hodnota el. odporu je na nich nejčastěji znázorněna textově (např. 1k2 znamená „jedno-kilo-dvě“ tedy 1200 ohmů) nebo graficky pomocí různobarevných proužků.
Často nás zajímá, jaký celkový odpor má více rezistorů v obvodu dohromady (např. pro výpočet celkového proudu obvodem). Záleží na tom, jestli jsou v obvodu spojeny sériově nebo paralelně.
Sériově zapojené rezistory
To znamená jeden za druhým (viz obrázek). Oběma mj. teče stejný proud I.
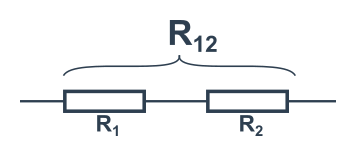
Z toho (a Ohmova zákona) se dá odvodit, že jejich celkový odpor je normálním součtem jednotlivých odporů. Tedy:
R_{12}=R_1+R_2
- Dva stejné rezistory s odporem R v sérii → celkový odpor 2R.
- Dva rezistory s odpory 100 Ω a 220 Ω v sérii → celkový odpor 320 Ω.
- Dva rezistory s odpory 2 kΩ a 2 Ω v sérii → celkový odpor 2,002 kΩ.
Paralelně zapojené rezistory
To znamená každý na jiné větvi proudu (tzv. vedle sebe, viz obrázek). Na obou musí být stejné napětí U.
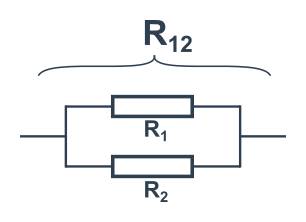
Z toho (a Ohmova zákona) se dá odvodit, že jejich celkový odpor splňuje rovnici:
\frac{1}{R_{12}}=\frac{1}{R_1}+\frac{1}{R_2}
Jde tedy o podobnou rovnici, ale s převrácenými hodnotami. Matematickými úpravami můžeme dojít k vyjádření R_{12} jako:
R_{12}=\frac{R_1R_2}{R_1+R_2}
- Dva stejné rezistory s odporem R paralelně → celkový odpor \frac{R}{2}.
- Dva rezistory s odpory 1 Ω a 4 Ω paralelně → celkový odpor \frac{1\cdot 4}{1+4}=\frac{4}{5}\,\mathrm{\Omega}.
- Dva rezistory s odpory 1 Ω a 100 Ω paralelně → celkový odpor \frac{1\cdot 100}{1+100}=\frac{100}{101}\,\mathrm{\Omega}\approx99\,\mathrm{\Omega}.
- Dva rezistory s odpory 100 Ω a 220 Ω paralelně → celkový odpor \frac{100\cdot 220}{100+220}=\frac{22 000}{320}\,\mathrm{\Omega}\approx69\,\mathrm{\Omega}.
Více rezistorů
Pro více rezistorů (a obecně více odporů) platí podobné vztahy.
Sériové zapojení N členů: R_{12..N}=R_1+R_2+R_3+\cdots+R_N
Paralelní zapojení N členů: \frac{1}{R_{12..N}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\cdots+\frac{1}{R_N}
(úprava do tvaru R_{12..N}= je samozřejmě možná, výsledné vzorce ale vypadají podle počtu rezistorů různě)
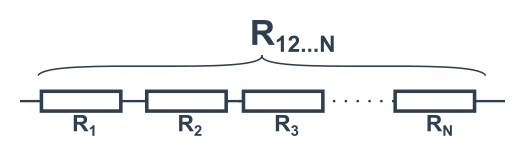
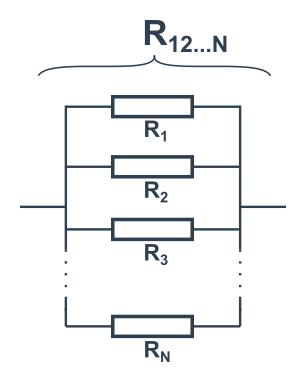
- Pět stejných rezistorů s odporem R v sérii → celkový odpor 5R.
- Tři rezistory s odpory 2 kΩ, 2 kΩ a 5 kΩ v sérii → celkový odpor 9 kΩ.
- Tři stejné rezistory s odporem R paralelně → celkový odpor \frac{R}{3}.
Složitější zapojení
Zjednodušujeme podle pravidel výše postupně od nejmenších vnitřních celků (dvojic).
Takto ano: 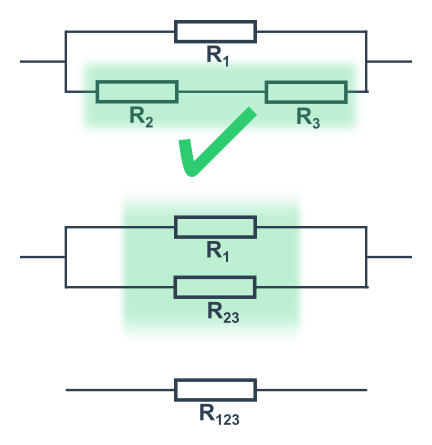
Takto ne (vybraná dvojice netvoří samostatné paralelní zapojení, k pravému uzlu se musí jít přes R_3):
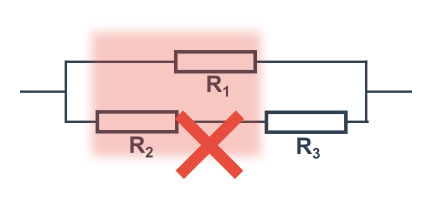
Zavřít















