Výpis souhrnů
Mechanika kapalin a plynů
Podtémata
Mechanika kapalin a plynů
Důležitou roli v mechanice kapalin a plynů hraje tlak. Obecně tento tlak můžeme rozdělit na
tlak vyvolaný (gravitační) tíhou samotné tekutiny (hydrostatický tlak u kapalin a atmosférický tlak u plynů)
tlak vyvolaný působením vnější síly na tekutinu v uzavřené nádobě (popisuje Pascalův zákon).
Celkový, nebo také absolutní tlak je pak součtem těchto dílčích tlaků.
1. Tlak vyvolaný tíhou tekutiny
Pokud něco neseme na hlavě, například těžký klobouk, cítíme jak na nás působí jeho tíha (neseme jej). Pokud si ale stoupneme my na klobouk (nezkoušejte!), jeho tíhu necítíme.
Podobně působí na tělesa ponořená v tekutině i tíha této tekutiny. A stejně jako v analogii s kloboukem je rozhodující jen ta část tekutiny, která se nachází nad tělesem. Projevem takového působení je tedy tlak tekutiny, který bude tím větší čím hlouběji je těleso ponořeno (tlačí větší sloupec tekutiny).
2. Tlak vyvolaný působením vnější síly
Je určen silou F a plochou S (například pístu), na kterou tato síla působí. Přenáší se do celého objemu kapaliny a je v celém tomto objemu stejný.
Toho využívají hydraulická zařízení, která fungují podobně jako jednoduché stroje. Pomocí různě velkých pístů převádíme sílu, takže například dokážeme sami zvednout auto (hydraulický zvedák).
NahoruHydrostatický tlak: základy
U kapalin je projevem jejího tíhového působení hydrostatický tlak. Jeho působením na plochu je hydrostatická tlaková síla.
Hydrostatický tlak značíme p_\mathrm h a závisí na hloubce pod hladinou h, přitažlivosti planety (tíhové zrychlení g) a na tom, o jak těžkou kapalinu jde (hustota \rho). Je to přímo součin:
p_\mathrm h=h\cdot\rho\cdot g
Hlavní rozdíl vůči tlaku vyvolanému vnější silou je ten, že není v celém objemu kapaliny stejný (roste s hloubkou).
Příklad: Tlak na dně bazénu
Plavecký bazén má hloubku 1,5 m. Jaký je hydrostatický tlak u dna?
- Chceme určit p_\mathrm h a známe hloubku bazénu h.
- Protože v zadání není nic navíc, máme nejspíš předpokládat, že se bazén nachází na Zemi a použijeme obvyklou hodnotu g\approx 10\,\mathrm{m/s^2}. Také bude asi napuštěn vodou a ne kyselinou. Tedy přibližně \rho\approx 1000\,\mathrm{kg/m^3}.
- Můžeme tedy dosadit do p_\mathrm h=h\cdot\rho\cdot g.
- p_\mathrm h=1{,}5\cdot 1000\cdot 10 \,\mathrm{Pa}=15 000\,\mathrm{Pa}.
- Hydrostatický tlak na dně je tedy 15 000 Pa.
Příklad: Mumie ponořená ve rtuti
Jaký hydrostatický tlak by drtil zlou filmovou mumii 1 m pod hladinou rtuti (hustota 13 500 kg/m³)?
- Hloubka h je 1 m a tíhové zrychlení g je přibližně 10 m/s².
- Jako \rho musíme použít hustotu rtuti (ne vody), tedy 13 500 kg/m³
- Dosadíme: p_\mathrm h=h\cdot\rho\cdot g= 1\cdot 13 500\cdot 10 \,\mathrm{Pa}=135 000\,\mathrm{Pa}.
- Stvůru tedy drtí 135 000 Pa.
Podle známé definice tlaku jako síly na plochu (p=F/S) můžeme odvodit i vzorec pro sílu vyvolanou hydrostatickým tlakem (působící na plochu S).
Do vzorce F=p\cdot S stačí jen dosadit hydrostatický tlak p_\mathrm h:
F= S \cdot h\cdot \rho\cdot g
Příklad: Síla na tělo potápěče
Jaká síla drtí tělo (1,8 m²) potápěče v hloubce 50 m pod vodou?
- Síla je F=p_\mathrm h\cdot S.
- Plochu S známe a z p_\mathrm h=h\cdot\rho\cdot g máme hloubku h. Za g a \rho dosadíme obvyklé hodnoty 10\,\mathrm{m/s^2} a 1000\,\mathrm{kg/m^3} (voda).
- Dosadíme F= S \cdot h\cdot \rho\cdot g = 1{,}8\cdot 50\cdot 1000\cdot 10\,\mathrm N
- Po vyčíslení dostaneme 900 000 N. Tedy 0,9 meganewtonu.
Zajímavosti
- Už v hloubce 10 m pod vodu je hydrostatický tlak stejně velký jako tlak celé atmosféry Země.
Archimédův zákon: intuitivně
Základní znění
Těleso ponořené do kapaliny je nadlehčováno vztlakovou silou. Její velikost se rovná velikosti tíhy kapaliny stejného objemu, jako je objem ponořené části tělesa.
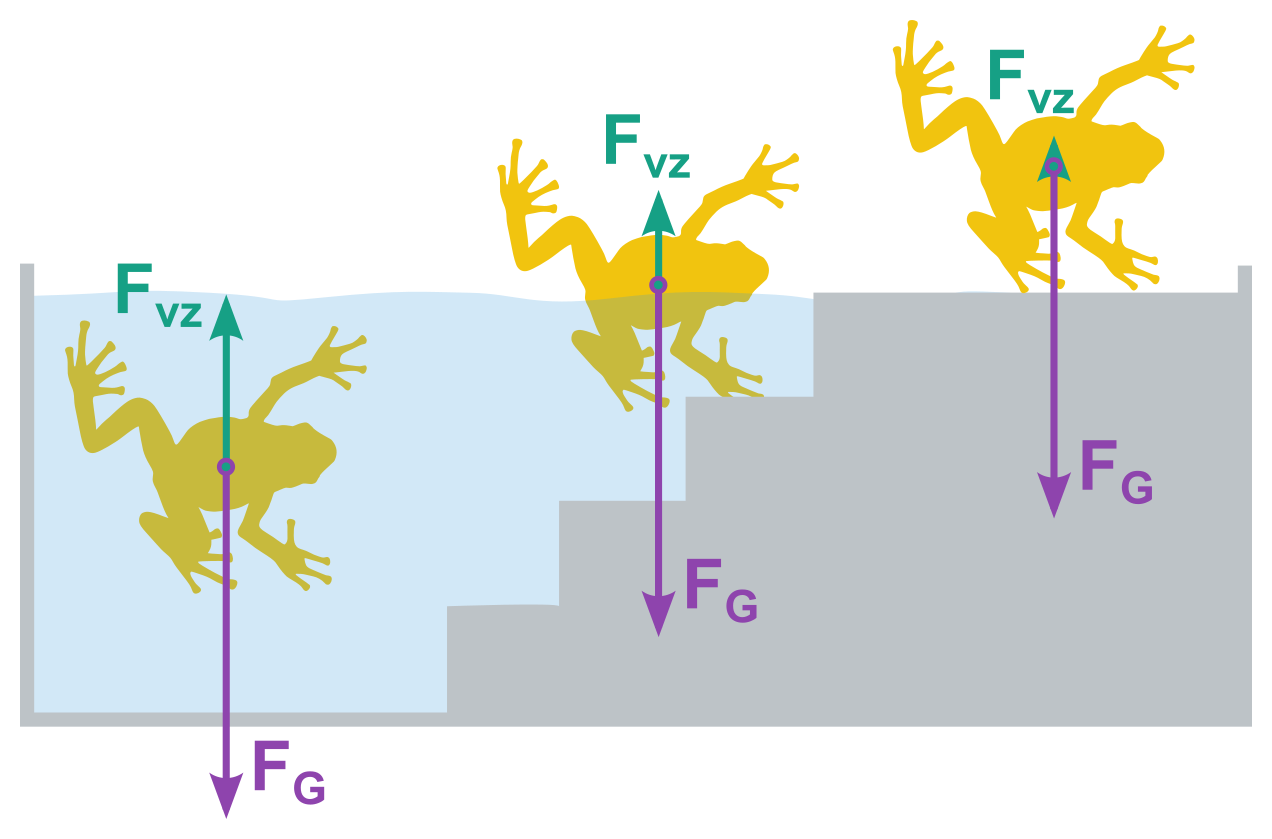
Platí jak pro kapaliny, tak pro plyny. Velikost vztlakové síly (F_\mathrm{vz}) je v plynech výrazně menší než v kapalinách kvůli jejich nižším hustotám.
F_{\mathrm{vz}} = V_{\mathrm{pod}} \cdot \rho_{\mathrm K} \cdot g
kde je g velikost tíhového zrychlení, V_{\mathrm {pod}} objem ponořené části tělesa a \rho_{\mathrm K} hustota kapaliny (případně plynu).
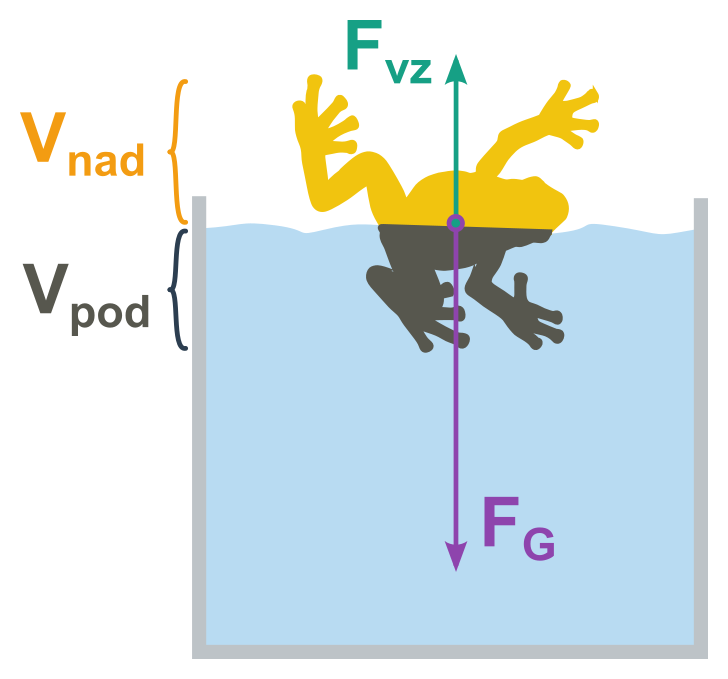
Těleso plovoucí po vodní hladině
Pro těleso plovoucí po hladině lze odvodit vztah mezi hustotami tělesa a kapaliny:
\frac{V_{\mathrm {pod}}}{V_{\mathrm {nad}} + V_{\mathrm {pod}}} = \frac{\rho_{\mathrm T}}{\rho_{\mathrm K}}
(\rho_{\mathrm T} je hustota tělesa, \rho_{\mathrm K} je hustota kapaliny, V_{\mathrm {pod}} je objem ponořené části tělesa a V_{\mathrm {nad}} + V_{\mathrm {pod}} = V je celkový objem tělesa.)
Příklady a využití Archimédova zákona
Archimédův zákon se uplatňuje v plynném prostředí, ale zejména v kapalném prostředí. Díky Archimédovu zákonu létají pouťové balonky i vzducholodě, na moři se nepotopí lodě, ponorky a ryby mohou ovlivňovat svůj pohyb ve vertikálním směru.
Tíha tělesa
- Při plavání určitě cítíte, že vás voda nadnáší. Vztlaková síla totiž působí na všechna tělesa – jak ve vodě, tak ve vzduchu.
- Proto když měříme „hmotnost“, zjistíme „váhu“ tělesa. Ta se od skutečné hmotnosti právě o tu nadlehčenou část.
- Rozdíl je ve vzduchu (\rho\approx 1{,}23\,\mathrm{kg/m^3}) jen nepatrný, ve vodě (\rho\approx 1000\,\mathrm{kg/m^3}) jej ale poznáme.
Pohyb pod vodou ve svislém směru
Archimédova zákona využívají k vertikálnímu pohybu ve vodě ryby. Jsou totiž vybaveny plynovým měchýřem.
Při pohybu ↑ jej nafouknou, a tím vzroste jejich V a tedy i F_\mathrm{vz}.
Při pohybu ↓ jej zase vyfouknou a F_\mathrm{vz} klesne.Stejně to děláme i my při potápění s bombou. Když se více nadechneme a nafoukneme plíce stoupáme vzhůru, když dýcháme mělce klesáme.
- Podobný princip využívají ponorky, ve kterých jsou instalovány vzduchové komory. Během ponoru jsou tyto komory naplněny vodou, a tedy je ponorka tažena dolů. Pro výnor se komory naplní vzduchem, čímž se její hmotnost výrazně sníží a velikost vztlakové síly převýší velikost síly tíhové.
Pohyb ve vzduchu ve svislém směru
- Letecké stroje využívají toho, že je jejich průměrná hustota menší než hustota vzduchu. Poznáme je hlavně díky tomu, že největší objem zaujímá vak nebo plynová nádrž.
- Vzducholodě byly plněny plynem s menší hustotou než vzduch, tedy vodíkem (v dnešní době se již nevyužívá), nebo heliem. Horkovzdušný balón zase využívá řídkého horkého vzduchu.
Zajímavosti
- Nezáleží na tom, jaký objem těleso vytlačilo vzhůru. Jelikož hydrostatický tlak závisí pouze na hloubce kvůli hydrostatickému paradoxu, je nejdůležitější objem ponořené části tělesa.
Atmosférický tlak
Pro tíhové působení plynů naší (nebo jiné) atmosféry definujeme atmosférický tlak. Princip je podobný jako u hydrostatického tlaku. I atmosférický tlak závisí na přitažlivosti (tíhovém zrychlení g), výšce atmosféry a její hustotě. Nemůžeme ale jednoduše použít stejný vzorec jako pro hydrostatický tlak, protože hustota plynu \rho není konstantní, výška atmosféry není jasně ohraničená a dokonce i g není v 60km výšce stejné jako u hladiny moře.
Platí alespoň, že čím výše se nacházíme, tím nižší atmosférický tlak tam bude (menší část vzduchového sloupce nad námi). Rozdíly se ale projeví až na větších výškových rozdílech, i kvůli malé hustotě vzduchu \rho\approx 1{,}2\,\mathrm{kg/m^3}.
U hladiny moře počítáme s tlakem kolem 100 000 Pa. Standardní hodnota je stanovena na 101 325 Pa. Znamená to také, že podle F=p\cdot S nám na 1 m² kůže působí síla 101 325 N. Naštěstí stejná síla působí i zevnitř těla (např. plíce), takže nejsme slisováni do malých masových kuliček.
Kromě pascalů se používají jednotky jako bar (1 bar = 100 000 Pa), atmosféra (1 atm. = 101 325 Pa) Často se atmosférický tlak také uvádí v neobvyklém násobku – hektopascalech (hPa).
Rozdíly v atmosférickém tlaku z velké části tvoří počasí (tlakové výše a níže, přesun vzduchu mezi nimi a vznik větru).
NahoruRovnice kontinuity
U proudění tekutin definujeme tzv. objemový průtok Q_V. Je to objem tekutiny, který proteče trubkou za jednotku času. Jednotkou je tedy m³/s a platí:
Q_V=\frac{V}{t}
Příklad: ropovod
Jaký byl průtok ropovodem, pokud za 1 minutu proteklo 30 m³ ropy?
- Známe V i t.
- Čas t není v základních jednotkách, musíme jej tedy převést na sekundy t= 60\,\mathrm s
- Dosadíme do Q_V=V/t
- Q_V=30/ 60 \,\mathrm {m^3/s}=0{,}5 \,\mathrm {m^3/s}.
- Průtok je 0{,}5 \,\mathrm {m^3/s} ropy.
Objem V je ale roven součinu průřezu trubice S a posunu kapaliny o dráhu s. Po dosazení máme Q_V=\frac{S\cdot s}{t}.
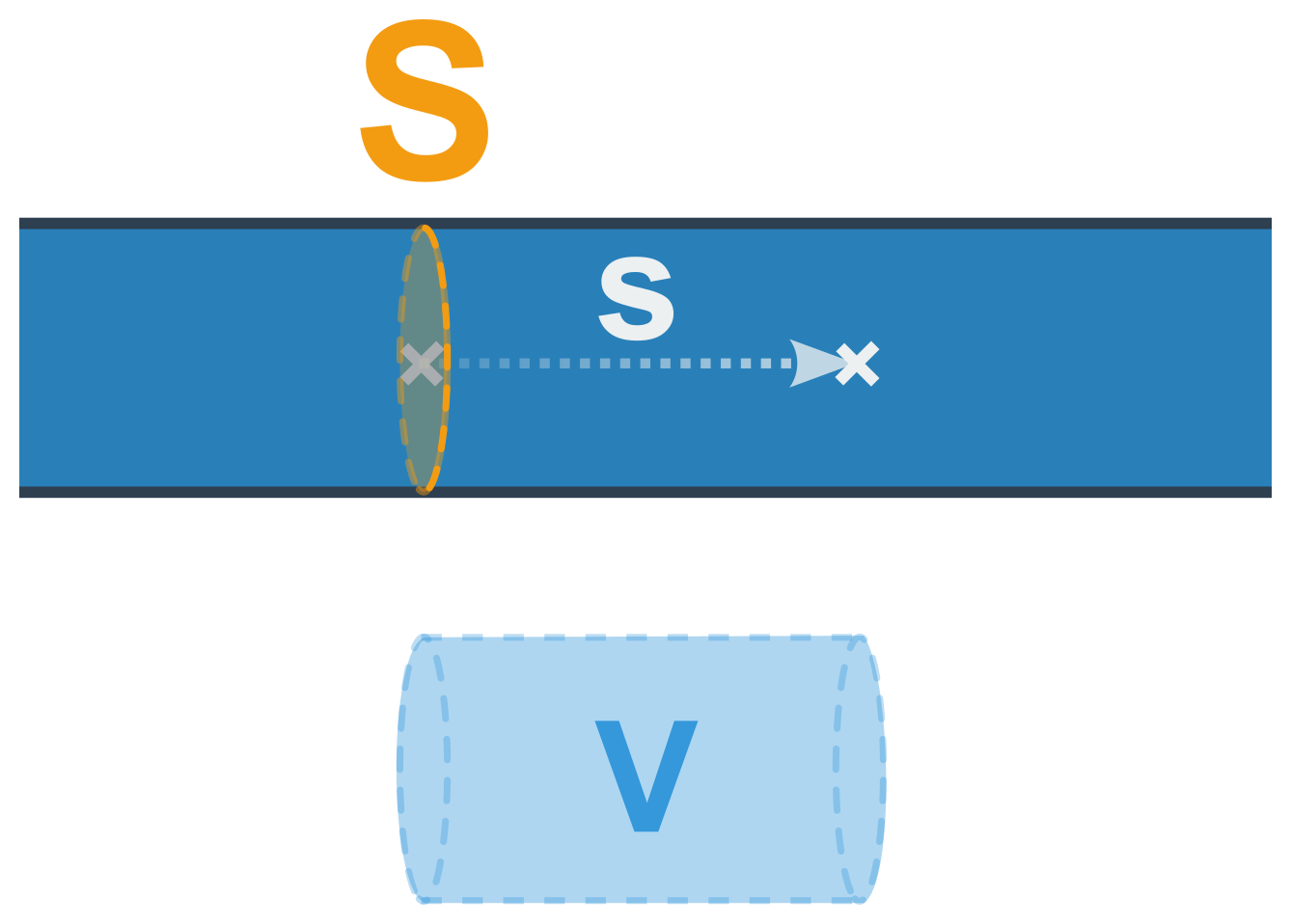
Víme přitom, že \frac{s}{t} je klasická definice rychlosti, tedy i rychlosti proudění v. Pak můžeme průtok zapsat ekvivalentní rovnicí:
Q_V=S\cdot v
Příklad: Lipno
Jaký průtok vody míří na turbínu vodní elektrárny Lipno I, pokud v její 15 m² přívodní šachtě proudí voda rychlostí 2 m/s?
- Známe S i v a to v základních jednotkách.
- Stačí tedy dosadit dosadit do Q_V=S\cdot v
- Q_V=15\cdot 2 \,\mathrm {m^3/s}=30 \,\mathrm {m^3/s}
- Průtok je 30 \,\mathrm {m^3/s}.
Protože jsou kapaliny nestlačitelné, musí být průtok Q_V v uzavřeném plném potrubí všude stejný (jinak by se někde musela hromadit).
Pokud tedy porovnáme dvě místa (Q_{V{,}1}=Q_{V{,}2}) a dosadíme za jednotlivé průtoky, vznikne známý vzorec rovnice kontinuity:
S_1\cdot v_1=S_2\cdot v_2
Příklad: stále stejně tlusté potrubí
Jak se mění rychlost ideální kapaliny při průchodu stále stejně tlustým potrubím?
- Nabízí se odpověď „všude stejná“. Ověříme to.
- Pro dvě místa v trubici platí S_1\cdot v_1=S_2\cdot v_2.
- Oba průřezy S_1 i S_2 jsou stejné, označme je tedy jednotně jako S.
- Máme S\cdot v_1=S\cdot v_2. V této rovnici můžeme krátit S.
- Dostaneme v_1=v_2. Tedy i rychlosti musí být stejné.
Příklad: přechod potrubí na třikrát větší průřez
Jak se změní rychlost ideální kapaliny při rozšíření potrubí na trojnásobný průřez?
- Nejprve přiřadíme jednotlivým místům v potrubí označení: užší část bude (1) a širší (2).
- Platí S_1\cdot v_1=S_2\cdot v_2.
- Víme že S_2=3\cdot S_1. Dosadíme to do rovnice.
- S_1\cdot v_1=3\cdot S_1\cdot v_2. Můžeme krátit S_1.
- Dostaneme v_1=3\cdot v_2. Hledáme ale rychlost v_2.
- Dělíme tedy 3 a dostaneme v_2=\frac{1}{3} v_1.
- Rychlost tedy bude třetinová.
Zajímavosti
- Přibližně platí i pro volně proudící kapalinu (řeka a její koryto).
- Někdy přibližně platí pro plyny (jsou stlačitelné).
- Obdobné rovnice kontinuity platí například i v elektřině (1. Kirchhoffův zákon).
- Rovnice V=S\cdot s je spolehlivá jen pro malé s (mohl by se změnit průměr trubice). Naštěstí rovnice Q_V=S\cdot v je už platná obecně.
Bernoulliho rovnice
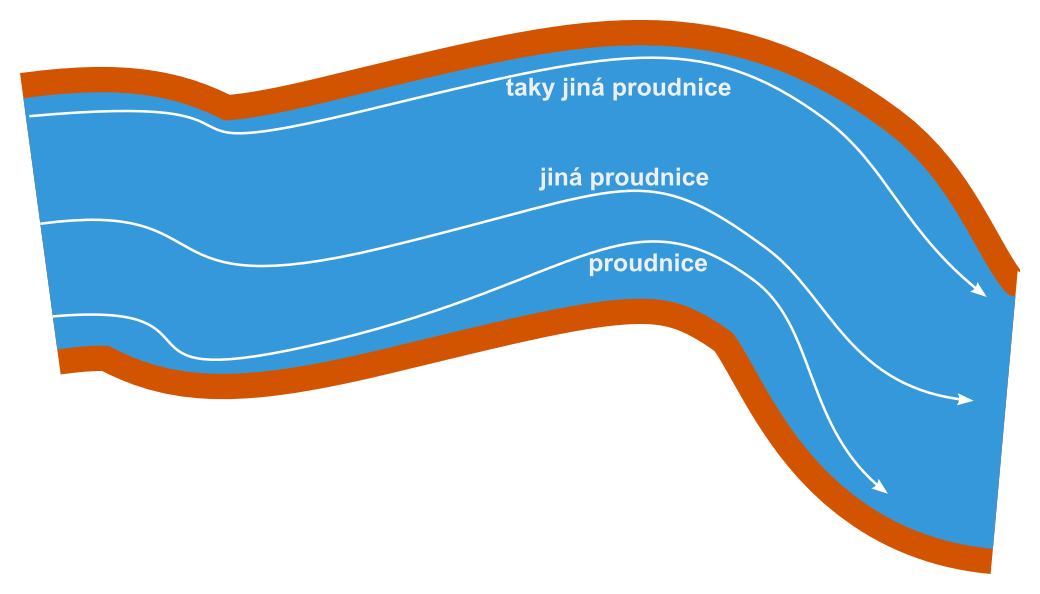
Bernoulliho rovnice popisuje souvislost mezi tlakem p v kapalině (o hustotě \rho) a rychlostí jejího proudění v. Podél jedné proudnice platí:
\frac{1}{2}\rho v^2+p = \mathrm{konst.}
Příklad: Zužující se trubice
Rychlost se v užší části trubice zvedla na dvojnásobek. Jak se tam změní tlak kapaliny?
- Protože se zvedla rychlost v, zvedla se i hodnota \frac{1}{2}\rho v^2 (\rho je u kapalin konstantní).
- Podle Bernoulliho rovnice má ale být \frac{1}{2}\rho v^2+p stále stejné. Musí tedy klesnout druhá část součtu – p.
- Odpověď tedy zní, že tlak klesne.
Pro dvě místa na téže proudnici tedy platí (pro konstantní hustotu):
\frac{1}{2}\rho v_1^2+p_1 = \frac{1}{2}\rho v_2^2+p_2
Příklad: Rychlost proudění podle změny tlaků
Voda proudí potrubím 1 m/s a má v něm tlak 5000 Pa. Jaký je tlak v části, kde voda proudí rychlostí 2 m/s?
- Platí \frac{1}{2}\rho v_1^2+p_1 = \frac{1}{2}\rho v_2^2+p_2.
- Známe všechno (voda má \rho=1000\,\mathrm{kg/m^3}) kromě p_2. To je naše neznámá, kterou musíme vyjádřit.
- Tlak p_2 osamostatníme odečtením \frac{1}{2}\rho v_2^2 od obou stran rovnice.
- Dostaneme: p_2=\frac{1}{2}\rho v_1^2+p_1-\frac{1}{2}\rho v_2^2
- Dosadíme: p_2=\frac{1}{2}1000\cdot 1^2+5000-\frac{1}{2}1000\cdot 2^2\,\mathrm{Pa}=500\cdot 1+5000-500\cdot 4\,\mathrm{Pa}=3500\,\mathrm{Pa}
- Tlak tedy klesne na 3500 Pa.
Pro jednoduchost obvykle definujeme Bernoulliho rovnici pro vodorovnou uzavřenou trubku.
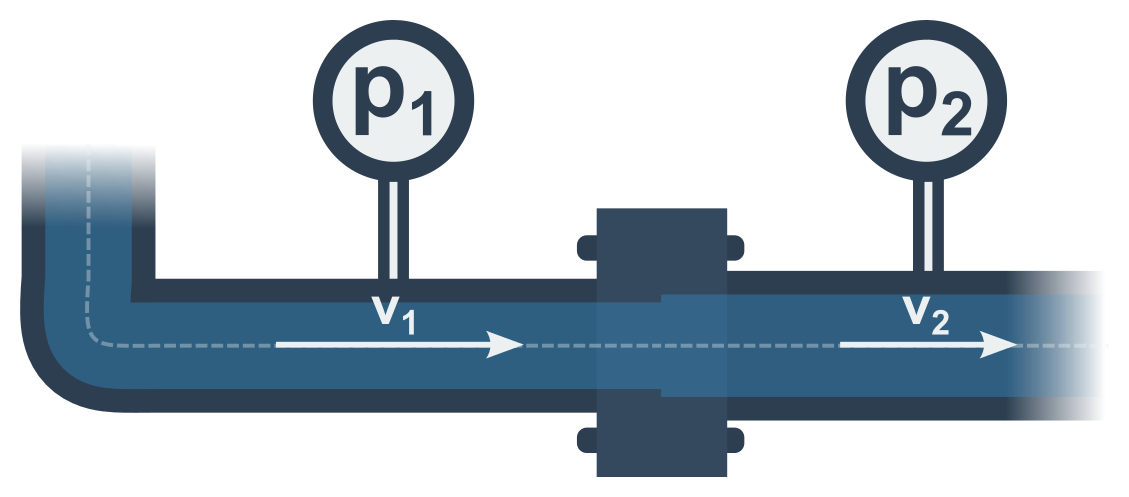
Jak by to bylo pro nevodorovnou trubku?
Pro nevodorovnou trubku bychom museli do rovnice započítávat i hydrostatický tlak p_h.
Bernoulliho rovnice vlastně říká, že zvýšením rychlosti proudění poklesne tlak. Tento princip platí i pro libovolné neturbulentní proudění kapaliny nebo plynu. Matematický vzorec sice v takovém případě neplatí přesně, ale jako odhad se hodí.
Tohoto principu se využívá v řadě případů, kde chceme vůči okolnímu prostředí vytvořit podtlak (fixírka, některé typy vývěv, profil křídla letadel).
Zajímavosti
Bernoulliho rovnice je vlastně rovnice zachování energie na jednotku objemu. Po vynásobení objemem je to ještě patrnější – získáte \frac{1}{2}m v^2 (kinetická energie) a p\cdot V=p\cdot S\cdot s=F\cdot s (práce/potenciální energie).
Vytékání kapaliny malým otvorem
Pomocí Bernoulliho rovnice (\frac{1}{2}\rho v_1^2+p_1 = \frac{1}{2}\rho v_2^2+p_2) můžeme odvodit rychlost tryskání vody z (malého) otvoru v nějaké nádobě.
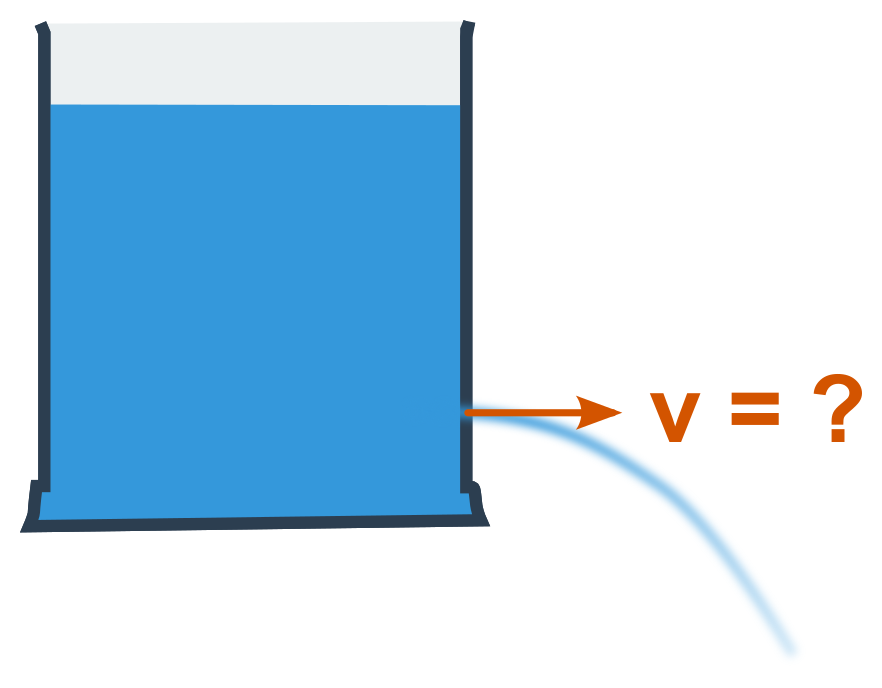
Zevnitř (index 1) je rychlost prakticky nulová a vně (index 2) je zase nulový tlak (pokud od obou stran odečteme atmosférický tlak). Po dosazení těchto nul do rovnice výše dostaneme p_1 = \frac{1}{2}\rho v_2^2.
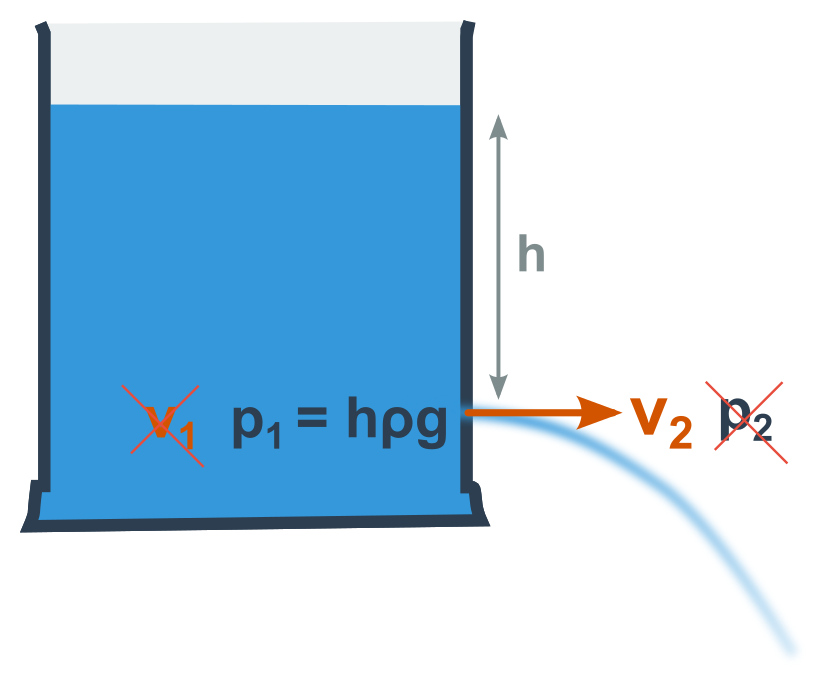
Tlak p_1 je vlastně hydrostatický tlak v nádobě (h\rho g) a rychlost zůstala jen jedna, nemusíme ji tedy indexovat. Máme h\rho g=\frac{1}{2}\rho v^2, z čehož vyjádříme rychlost:
v = \sqrt{2 h g}
Příklad: dvojnásobná hloubka
- Bude z otvoru v dvojnásobné hloubce nebude stříkat voda dvakrát rychleji?
- Podle vzorce v = \sqrt{2 h g} závisí rychlost na odmocnině z hloubky.
- Pokud tedy změníme h na 2h, dostaneme v = \sqrt{2\cdot 2 h g}= \sqrt{2}\cdot \sqrt{2 h g}.
- Rychlost tedy bude jen \sqrt 2-krát větší.
Příklad: stav beztíže
- Jaká bude rychlost stříkání vody z děravé lahve ve stavu beztíže?
- Ve stavu beztíže je g nulové.
- Do v = \sqrt{2 h g} tedy dosazujeme nulu. A součin s nulou je nulový celý.
- A odmocnina z nuly je nula. Rychlost tedy bude nulová – ve stavu beztíže voda samovolně nevytéká.
Tlak a tlaková síla
Definice
Tlak (značíme p) je veličina popisující deformační (ne pohybové) účinky síly na těleso. Je definován pomocí tlakové síly \vec F působící kolmo na určitou plochu S.
p = \frac{F}{S}
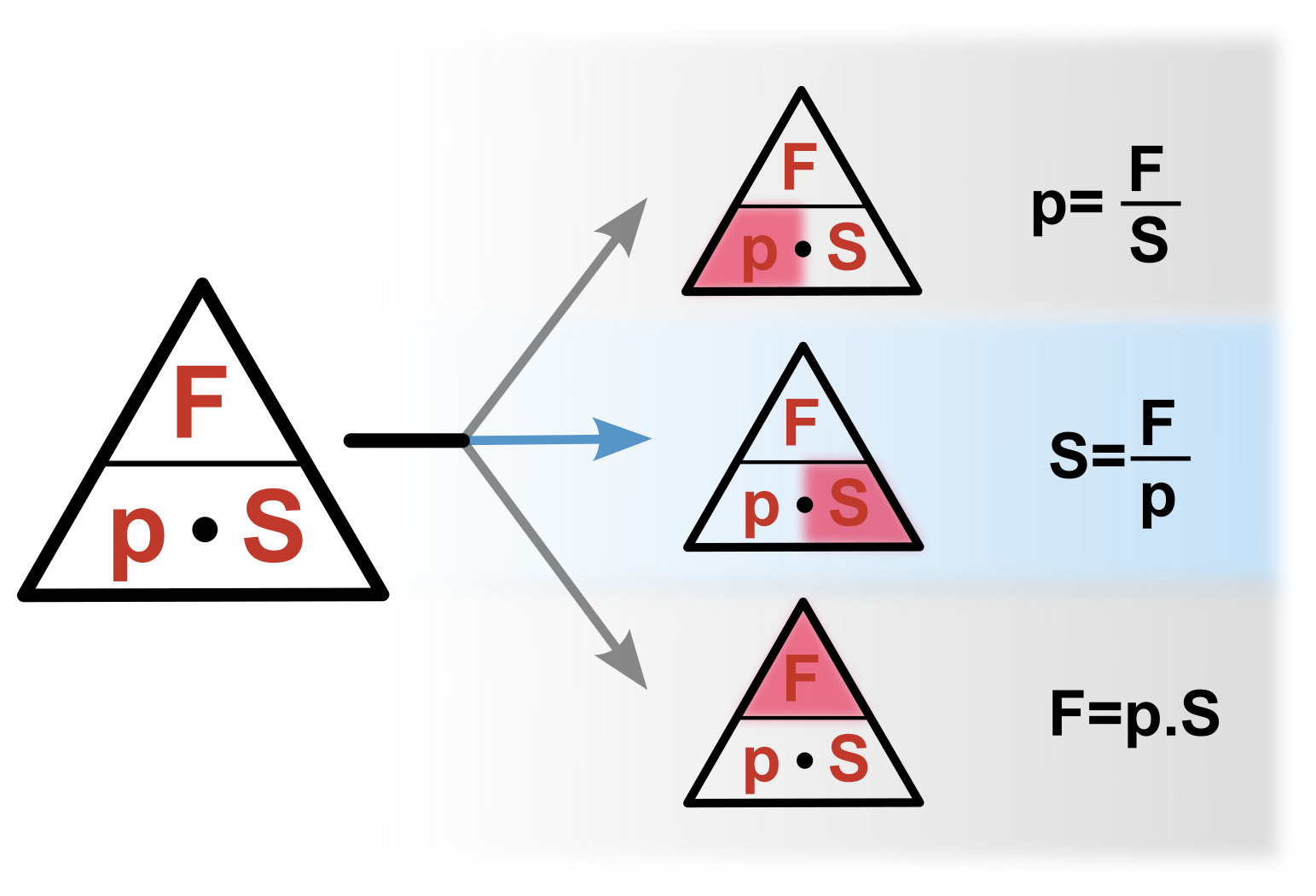
Úpravou rovnic (nebo pomocí vztahového trojúhelníku níže) můžeme odvodit další vztahy:
F = p \cdot S
S = \frac{F}{p}
Jednotky
Jednotkou je (jak ze vztahu p = F/S vyplývá) newton na metr čtvereční (N/m²). Tato jednotka dostala také vlastní název – pascal.
Typicky se setkáváme se silami v jednotkách až stovkách newtonů působícími na plochy mnohem menší než je metr čtvereční. Proto se kolem nás setkáváme nejčastěji s tlaky v tisících, ne-li milionech pascalů.
Vtip o jednotkách
Archimedes, Pascal a Newton hrají na schovávanou. Archimedes piká. Pascal se rychle schová do křoví.
Newton se vůbec neschovává, jen do hlíny klackem namaluje čtverec metr krát metr a postaví se do něj.
Archimedes dopiká, okamžitě uvidí Newtona a volá: „Deset dvacet Newton!“
Newton v klidu řekne: „Nene. Newton na metr čtvereční je přece pascal!“
Vztahový trojúhelník
Pro získání vzorce pro libovolnou veličinu p, F, S můžeme použít vztahový trojúhelník (pyramidu). Více o tom jak se vytváří a funguje najdete zde.
Zajímavost: Jednotka SI
Jednotka pascal je v soustavě SI teprve od roku 1971.
Poznámka: Ne vždy lze jednoduše znázornit tlakovou sílu s působištěm v místě doteku (např. více končetin). Proto v některých příkladech používáme k ilustraci i tíhovou sílu s působištěm v těžišti. Má totiž stejnou velikost jako tlaková síla, kterou vyvolává.
Nahoru
