Čeština
Matematika
Angličtina
Informatika
Biologie
Němčina
Umíme to
Zeměpis
Chemie
Dějepis
Fyzika
ZSV
Biologie
Zeměpis
Chemie
Dějepis
Fyzika
ZSV
Rozhodovačka
Otázky
Slepé mapy
Pexeso
Přesouvání
Rozřazovačka
Řazení
Poznávačka
Krok po kroku
Vpisování
Porozumění
Doplňování textu
Pojmy ve větách
Označování
Situace
Poznávání zvuků
Křížovky
Roboti
Tetris
Tipovačka
Týmovka
Závody
Odkrývačka
Můj účet
Odhlásit se
Předcházející
Navazující
V plynech může docházet (interakcí s okolím) k procesům, kdy se mění jednotlivé stavové veličiny. To je děj v plynu.
Během děje v ideálním plynu platí stavová rovnice pV=nRT. Pro uzavřené systémy (stálé množství plynu) je konstantní R i n a máme tři proměnné stavové veličiny (p, V a T).
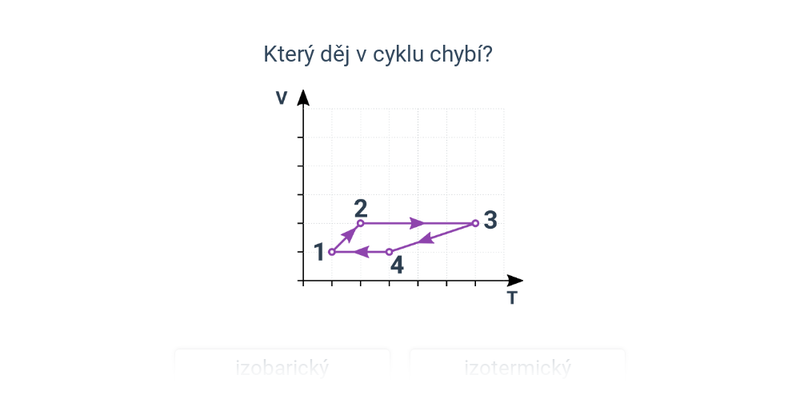
Často dokážeme ještě jednu z nich zafixovat (například objem pevnou velikostí nádoby). Těmto nejjednodušším dějům s pouze dvěma proměnnými stavovými veličinami říkáme izochorický děj (stálý objem), izotermický děj (stálá teplota) a izobarický děj (stálý tlak).
Významným dějem je i adiabatický děj (u něj je konstantní tzv. entropie).
Izochorický děj (konstantní V)
Upravíme stavovou rovnici na \frac{p}{T}=\frac{nR}{V} (dělením obou stran výrazem VT). Pravá strana jsou samé konstanty, je tedy celá konstantní:
\frac{p}{T}=\mathrm{konst.}
Pro libovolné okamžiky (nebo stavy) 1 a 2 během tohoto děje tedy platí \frac{p_1}{T_1}=\frac{p_2}{T_2}. Jde vlastně o přímou úměru mezi p a T. Pokud se např. T postupně zdvojnásobuje, p současně roste také na dvojnásobek.
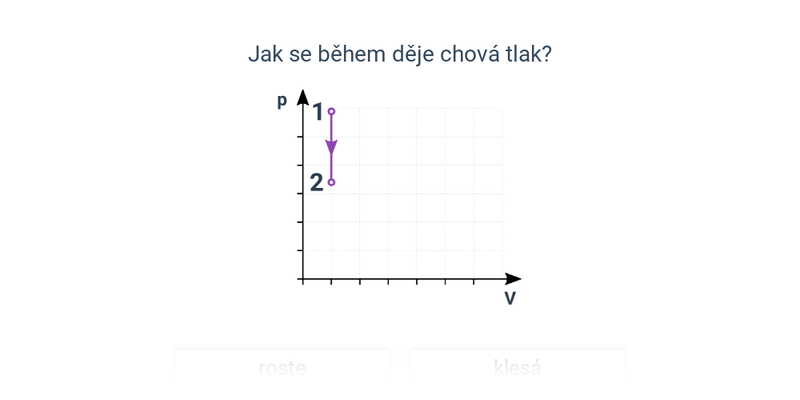
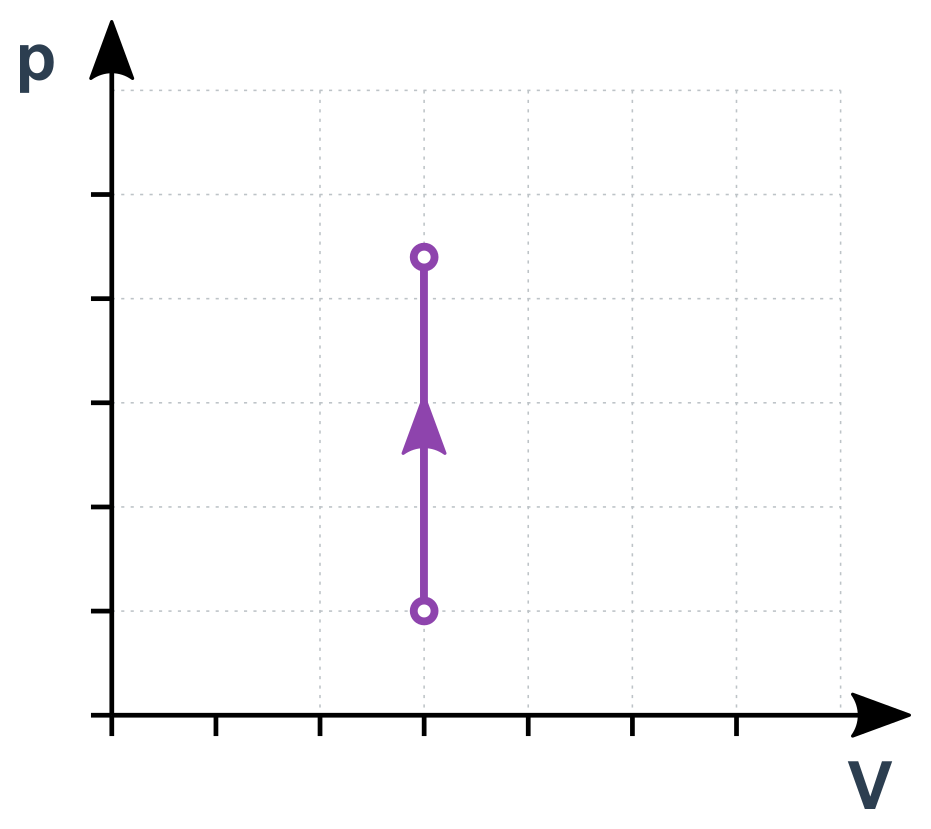
Izochorický děj v p-V diagramu
Izotermický děj (konstantní T)
Konstantou je T, a tedy i celá pravá strana stavové rovnice:
p\cdot V=\mathrm{konst.}
Pro dva stavy 1 a 2 platí p_1\cdot V_1=p_2\cdot V_2. Jde vlastně o nepřímou úměru mezi p a V (zvětšením V na dvojnásobek klesne p na polovinu). Změny musí probíhat dostatečně pomalu, aby “topení” stíhalo udržovat plyn na stálé teplotě. Jinak by šlo o jev adiabatický (viz níže).
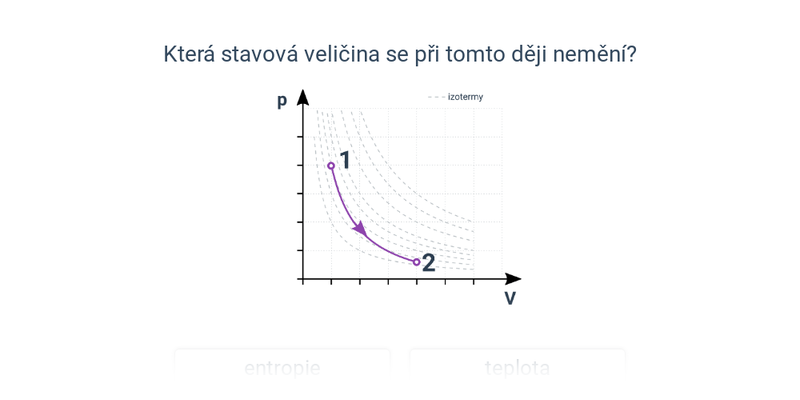
Izotermický děj v p-V diagramu
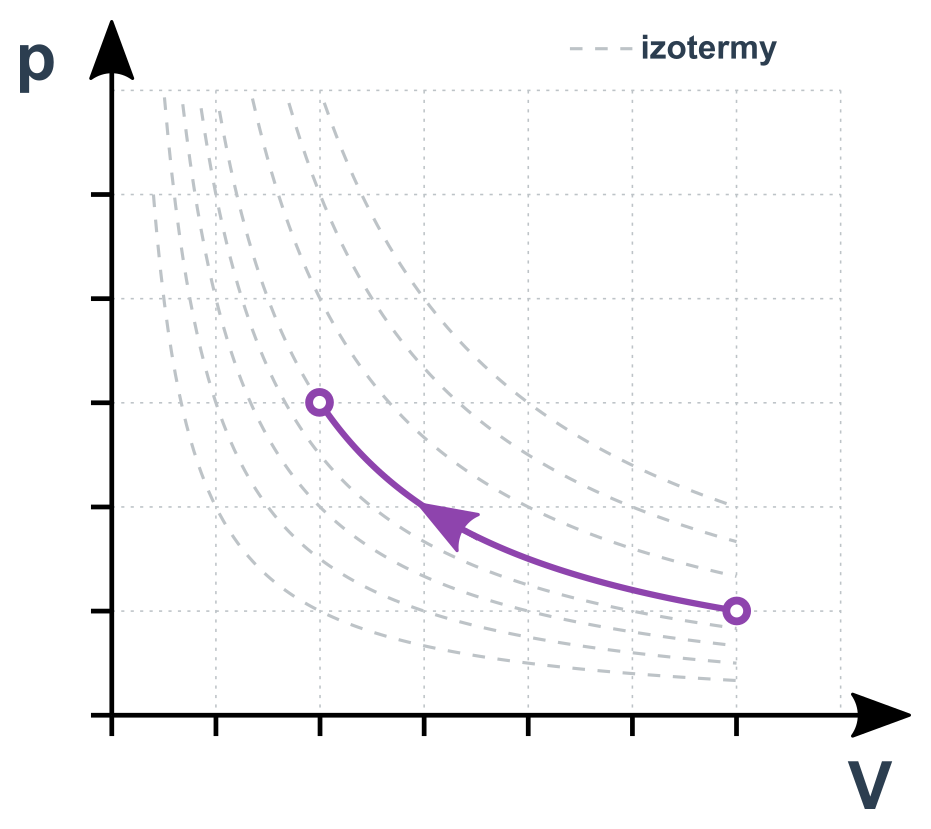
Izobarický děj (konstantní p)
Upravíme stavovou rovnici na \frac{V}{T}=\frac{nR}{p}. Pravá strana jsou opět samé konstanty, je tedy celá konstantní:
\frac{V}{T}=\mathrm{konst.}
Pro stavy 1 a 2 můžeme psát \frac{V_1}{T_1}=\frac{V_2}{T_2}. Jde vlastně o přímou úměru V a T. Pokud se T zdvojnásobí, V bude taky dvojnásobný).
Izobarický děj v p-V diagramu
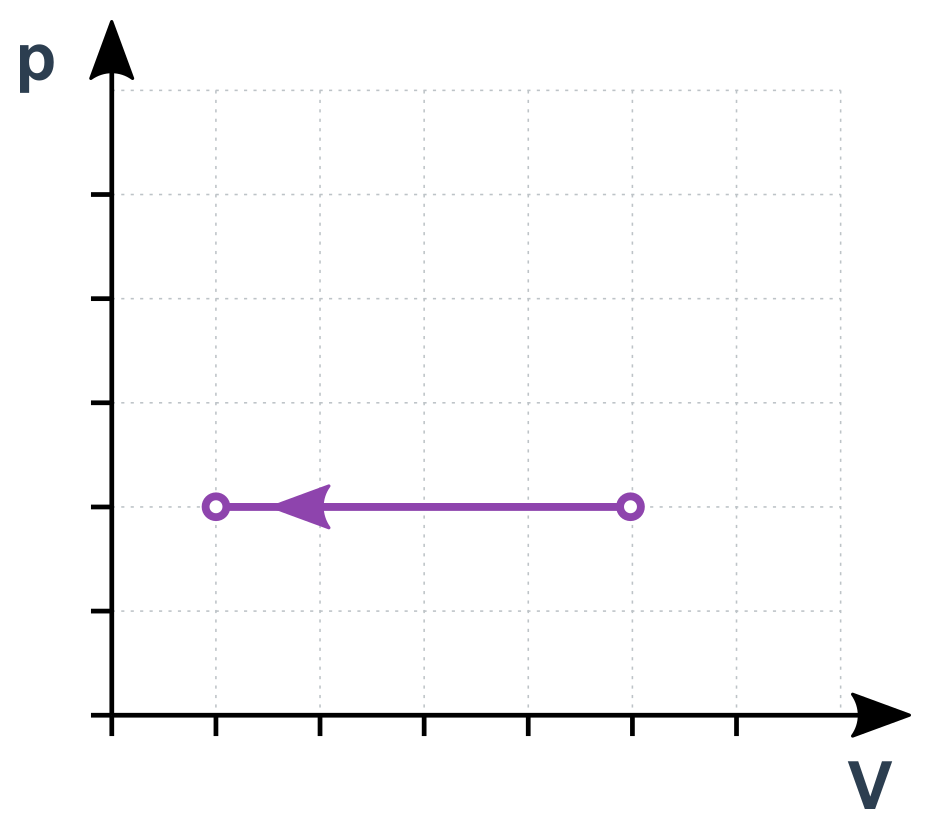
Adiabatický děj
Popisuje rychlou expanzi/stlačení plynu. Vztah uvádíme přímo:
p\cdot V^\kappa =\mathrm{konst.}
Pro jednoatomové plyny je \kappa=5/3, pro dvouatomové pak \kappa=7/5. Pro stavy 1 a 2 můžeme psát p_1\cdot V_1^{\kappa}= p_2\cdot V_2^{\kappa}.
Teplota při expanzi klesá (také proto deodoranty studí) a při stlačení roste (až ke vznícení paliva ve válci diesel motoru).
Adiabatický děj v p-V diagramu
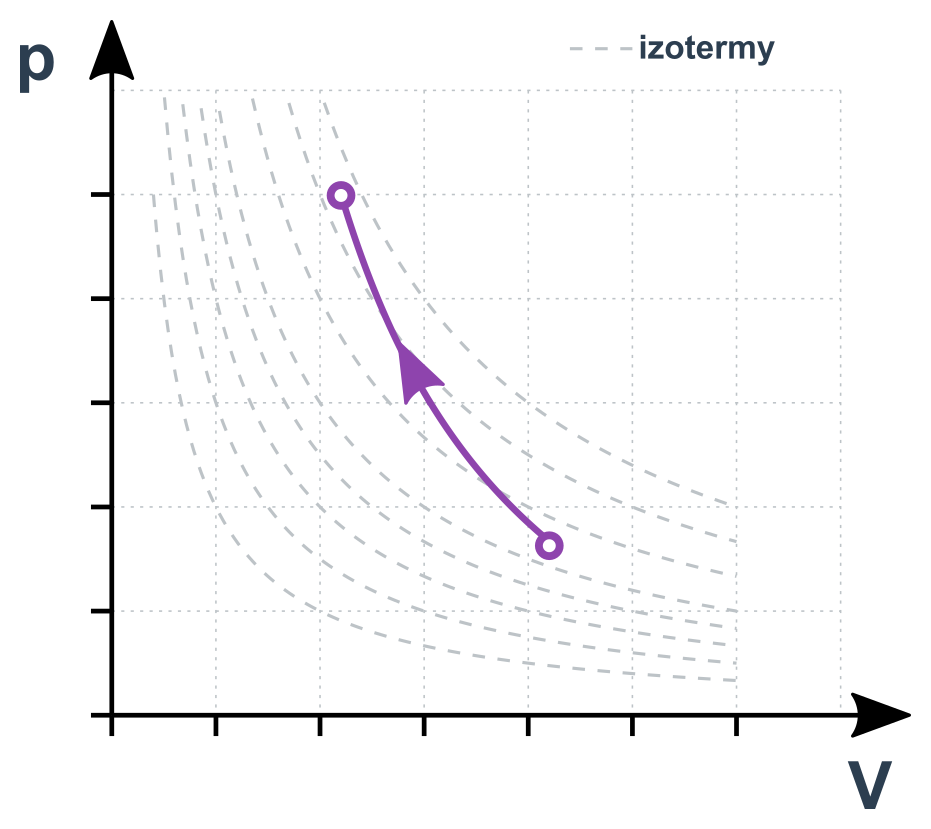
Zajímavosti
- Prakticky je nejsnáze dosažitelný děj izochorický (např. plyn uzavřený v pevné nádobě) a adiabatický (volná, rychlá nekontrolovaná expanze/stlačení).
- Pomocí p\cdot V^\kappa =\mathrm{konst.} a stavové rovnice pV=nRT můžeme vyjádřit pro adiabatický děj další vztah p\cdot T^{\frac{\kappa}{1-\kappa}}=\mathrm{konst.}
- Adiabatický děj (a pokles teploty při volném rozpínání) se používá k ochlazení zkapalňovaných plynů.
- Exponent \kappa je podíl měrného skup. tepla při stálém objemu a při stálém tlaku \kappa=c_\mathrm p/c_\mathrm V.
- Proč máme dvě verze stavové rovnice? Je to možné proto, že R byla definována jako R=k\cdot N_A a n = N/N_A (s Avogadrovou konstantou N_A). Po dosazení těchto výrazů za R a n do původní stavové rovnice p V = nRT získáme právě p V = NkT.
