Výpis souhrnů
Dynamika (příčiny pohybu)
Podtémata
Dynamika (příčiny pohybu)
Dynamika je část mechaniky, která se snaží vysvětlit, co způsobuje pohyb (přesněji jeho změny).
Základním pojmem je síla, což je působení okolí na těleso. Má velikost (jak moc působí) a směr (kterým směrem mě například táhne). Síly působící na stejné těleso často sčítáme (neboli skládáme) do jedné výsledné síly. Souvislost výsledných sil s pohybem popisují Newtonovy pohybové zákony.
Síla může mít různý původ (mechanický tah provazu, neviditelná přitažlivá síla magnetu, …), rozeznáváme tedy různé typy sil. Některé konkrétní typy sil, kterými se zabýváme samostatně:
- Ve vesmíru počítáme s gravitačními silami.
- Na Zemi je gravitace doplněna odstředivou silou otáčení země na tíhovou sílu. Definujeme taky tzv. tíhu.
- Stlačování těles (například opěrky sedadla našimi zády) popisuje tlaková síla a s ní související veličina tlak.
- Pokud po sobě dva povrchy klouzají dochází k smykovému tření, které můžeme popsat třecí silou.
Pokud se nezajímáme jen o posuvný pohyb těles, mohou mít síly i otáčivé účinky. To popisuje veličina moment síly, pomocí které můžeme otáčení těles i vypočítat.
Kromě sil definujeme v dynamice taky veličinu zvanou hybnost, která se hodí zejména pro popis soustavy více těles.
NahoruSkládání sil
Skládání, neboli sčítání sil je nejčastěji potřeba, když zjišťujeme výslednou sílu působící na těleso. Protože síla je vektorová veličina, skládání sil je vlastně sčítáním vektorů. Proto následující odstavce platí i pro jakoukoliv jinou vektorovou veličinu (např. hybnost, moment síly, …).
U sčítání více sil (F_1, F_2, F_3, …) často výslednou sílu označujeme bez indexu (F), v příkladech níže ji ale pro jednoznačnost označíme indexem „celk“.
Síly ležící v jedné přímce
Nejjednodušší je, když leží všechny síly v jedné přímce (např. všechny míří vodorovně doprava nebo doleva):
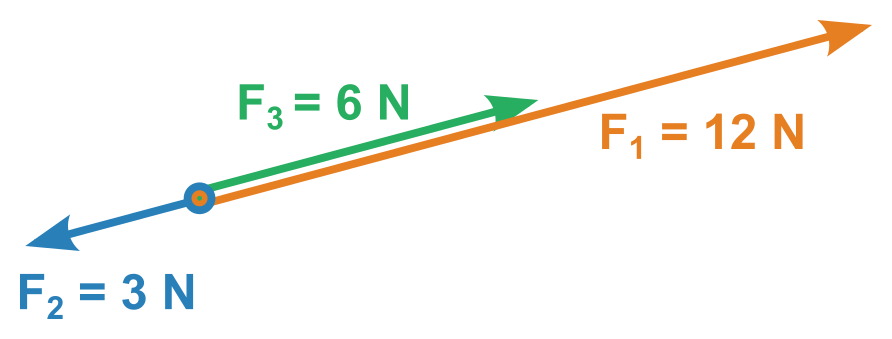
- Zvolíme směr (jeden z těch dvou).
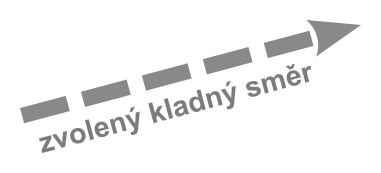
- Přičítáme velikosti sil mířících zvoleným směrem, a odečítáme ty opačné.
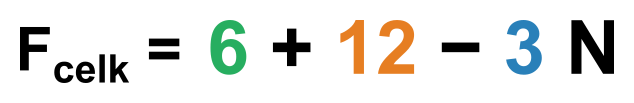
- Vyjde nám velikost (délka) výslednice. Pokud je kladná, míří námi zvoleným směrem, pokud ne, míří na druhou stranu.
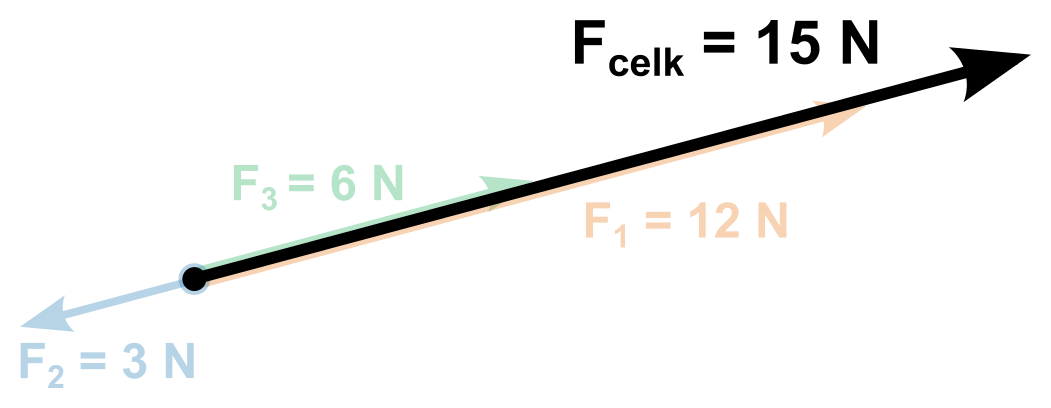
Dvě síly neležící v jedné přímce (grafické řešení)
- Síly narýsujeme tak, aby vycházely z jednoho bodu/působiště
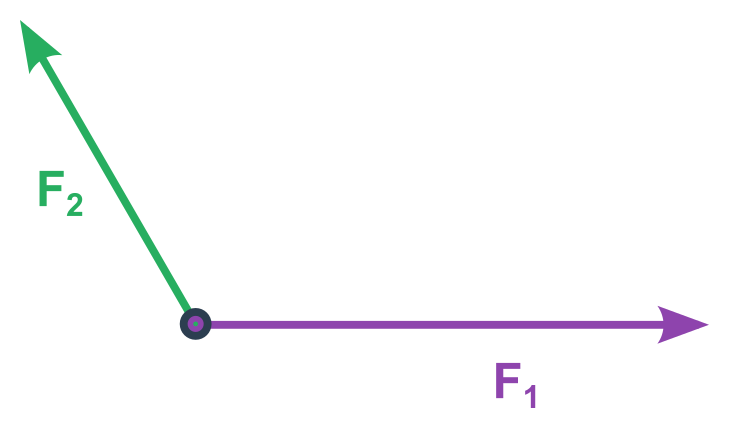
- Doplníme na rovnoběžník. Výsledkem je jeho úhlopříčka vycházející ze společného počátku sil
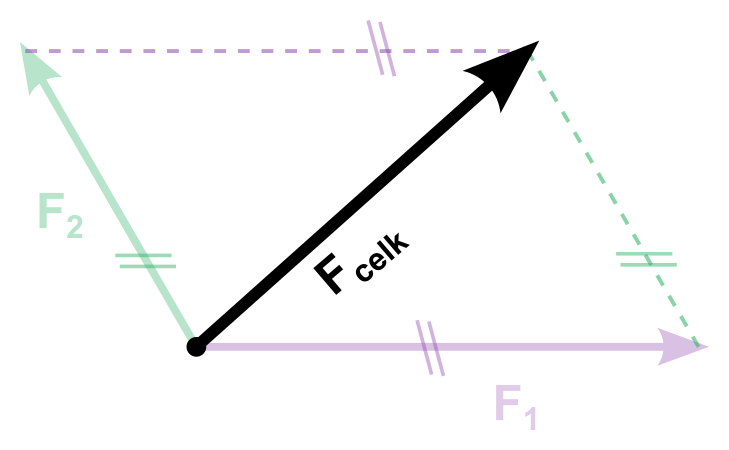
Pokud jsou na sebe síly kolmé, jde o úhlopříčku obdélníka s délkou podle Pythagorovy věty F=\sqrt{F_1^2+F_2^2}.
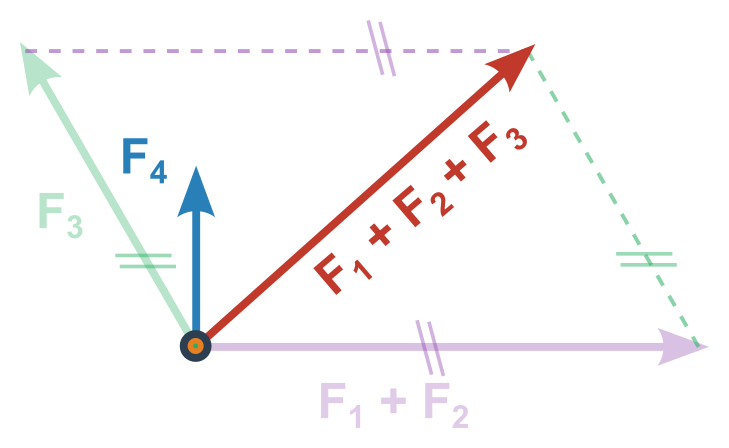
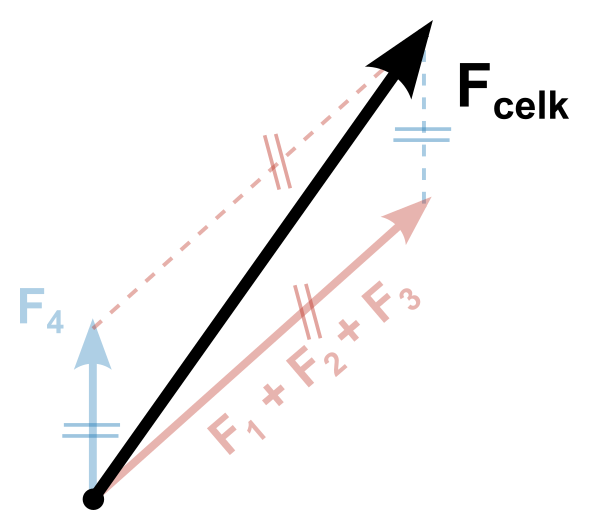
Více sil neležících v jedné přímce (grafické řešení)
- Vektory narýsujeme tak, aby vycházely z jednoho bodu/působiště
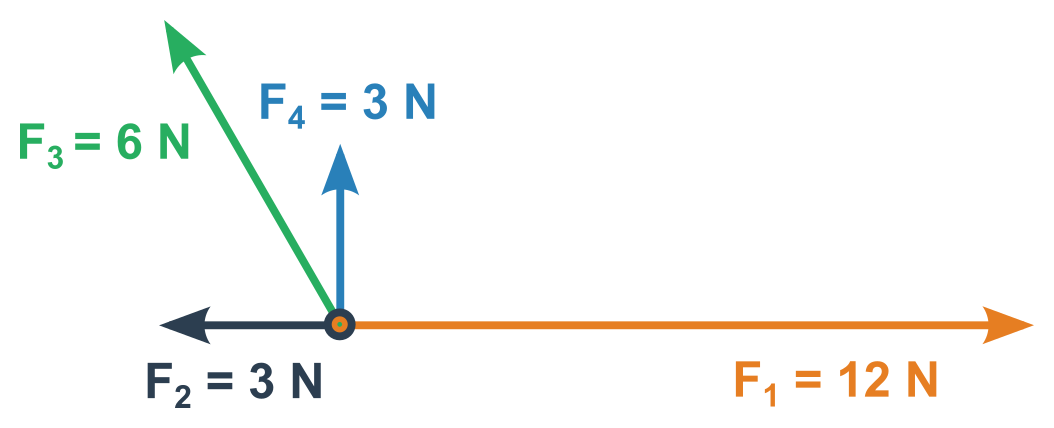
- Doplňováním na rovnoběžník sčítáme postupně jednotlivé vektory dokud nezbyde jeden výsledný vektor (pořadí je na nás, nejjednodušší je ale sdružovat rovnoběžné síly a následně ty na sebe kolmé)
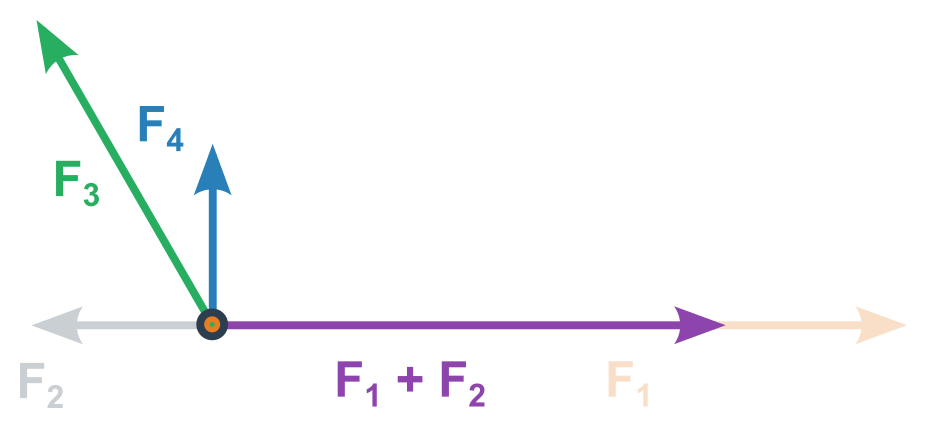
Souřadnicové řešení
- Musíme zvolit nějakou kartézskou soustavu souřadnic, například ve směru jedné ze sčítaných sil.
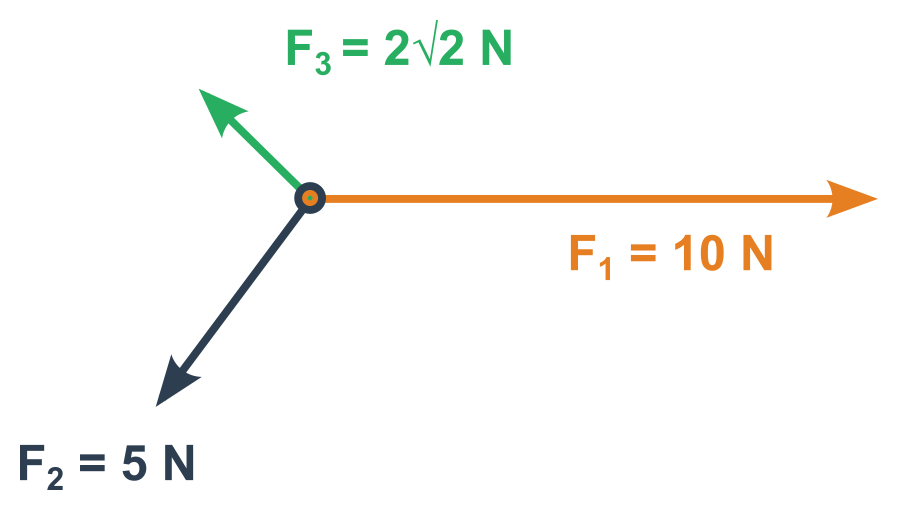
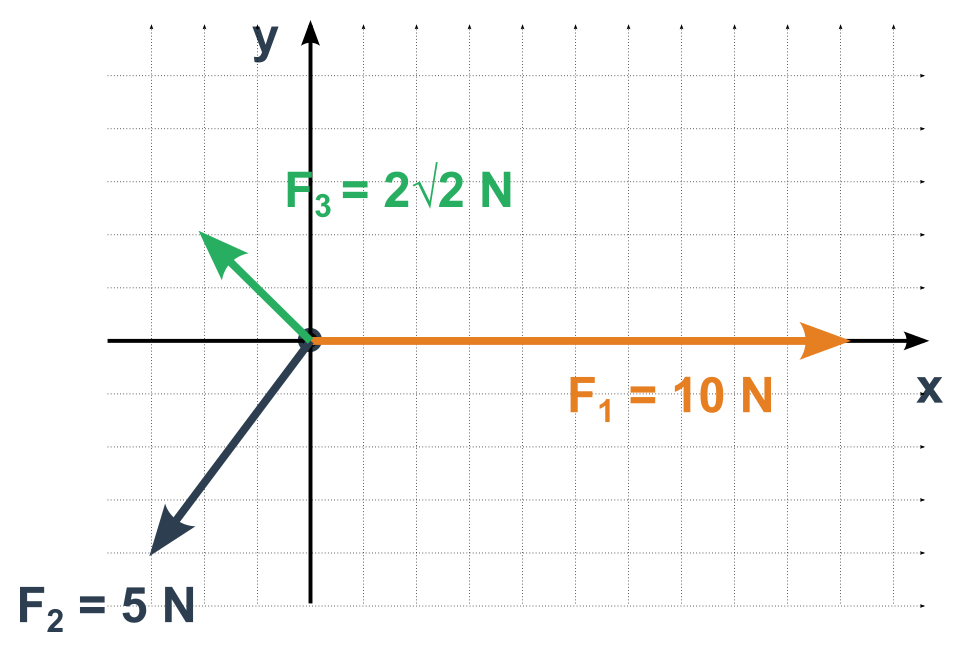
- Určíme jednotlivé složky všech vektorů sil v této soustavě
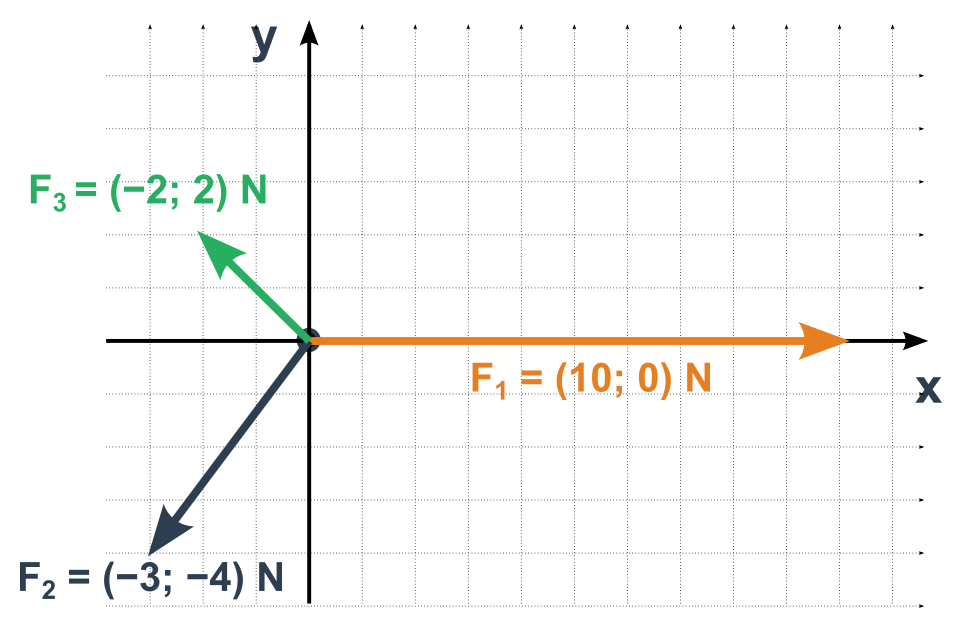
- Sečteme zvlášť stejné složky všech sil

- Výsledkem je vektor výsledné síly o souřadnicích které nám vyšly
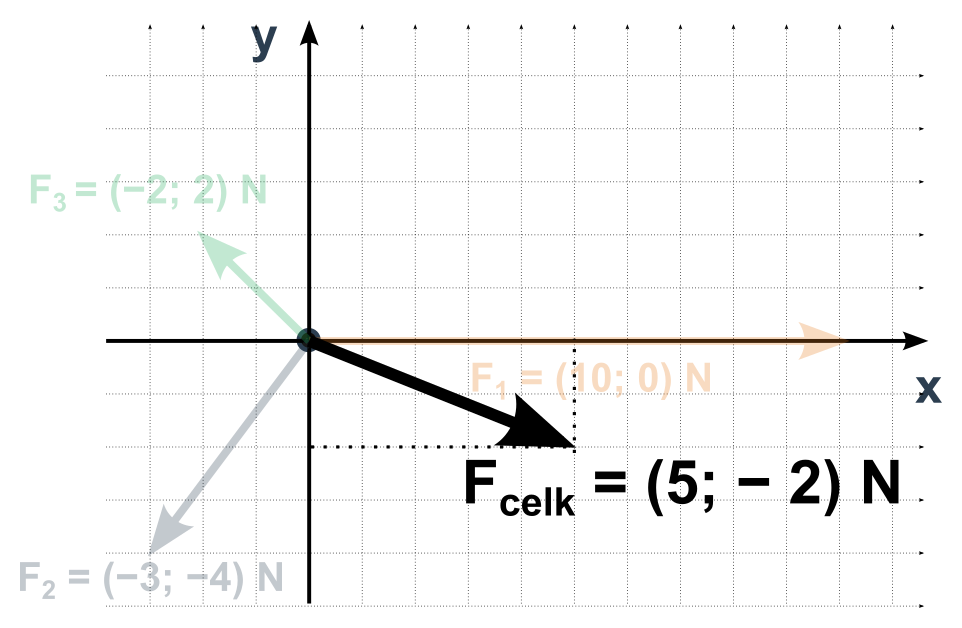
Velikost je podle Pythagorovy věty odmocnina z druhých mocnin souřadnic (zde odmocnina z 5^2+(−2)^2, tedy \sqrt{29}).
Tipy
Pokud jsou na sebe dvě síly kolmé, určíme délku výsledné síly i se znalostí úhlopříček obdélníka (Pythagorova věta, F_\mathrm{celk}=\sqrt{F_1^2+F_2^2})
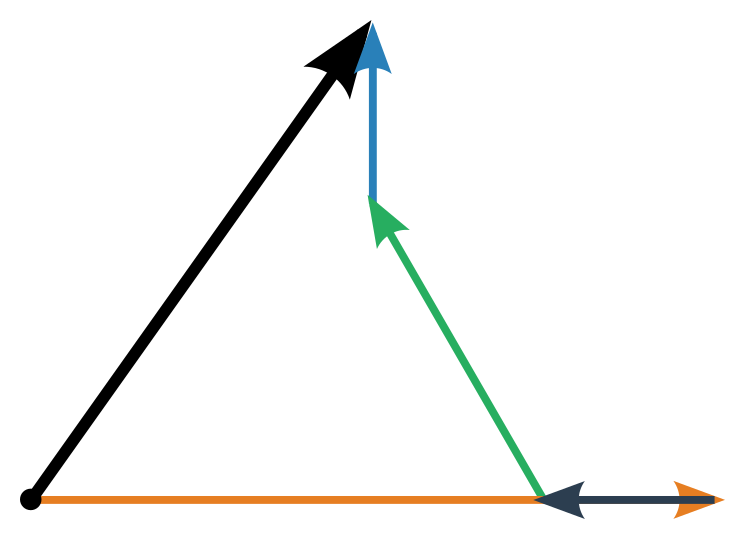
Alternativně můžeme grafické skládání sil pojmout tak, že síly připojujeme jednu za druhou jako na řetěz (viz obrázek). Je to sice názornější, ale rýsovalo by se to mnohem hůř.

Newtonovy pohybové zákony
Newtonovy zákony jsou pravidla, která popisují vztah pohyb tělesa – síly na těleso působící. Jsou tři:
- První Newtonův zákon: Zákon setrvačnosti – vysvětlí, proč se musíme v autobuse držet, když stojíme.
- Druhý Newtonův zákon: Zákon síly – ukazuje přímou úměru mezi součtem sil působících na těleso a jeho zrychlováním.
- Třetí Newtonův zákon: Zákon akce a reakce – aneb, když nás táhne gravitace k zemi, my táhneme zeměkouli stejnou silou nahoru.
Zákon setrvačnosti
Také známý jako první Newtonův zákon. Jeho původní znění je v latině, překlad je přibližně následující:
Těleso setrvává v klidu nebo rovnoměrném pohybu v daném směru, není-li nuceno vnějšími silami tento stav změnit.
„V daném směru“ znamená především rovnoměrný přímočarý pohyb (konstantní vektor rychlosti \vec v). Může mít ale i další význam (viz Zajímavosti).
Těleso není „…nuceno vnějšími silami tento stav změnit…“ právě tehdy, když je výslednice (vektorový součet všech sil působících na těleso), nulová.
\vec F_1+\vec F_2+\vec F_3+\dots=\vec 0 \;\;\;\implies\;\;\; \vec v=\mathrm{konst.}
Tento zákon platí jen v inerciálních soustavách.
Důsledky
- Pokud je výslednice sil nulová, vektor rychlosti \vec v se nemění. Ani jeho velikost, ani jeho směr.
- Pohyb za nepřítomnosti sil sám nezastaví.
- I za přítomnosti sil může být pohyb/klid tělesa neměnný (pokud je jejich výslednice nulová).
Zajímavosti
Původní znění je „Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus illud a viribus impressis cogitur statum suum mutare.“
Výzkum původních Newtonových děl ukazuje , že první zákon zahrnuje i setrvačnost otáčivého pohybu a tedy není jen speciálním případem druhého Newtonova zákona¹. Příklady spojenými s rotací se nicméně cvičení nezabývají.
Zákon síly: se vztahy
Také je znám jako druhý Newtonův zákon, je jedním z nejdůležitějších zákonů, které popisují dynamiku pohybu (proč objekty mění svůj pohyb).
Matematicky je vyjádřen jako rovnice mezi výslednicí sil působících na těleso (\vec F), jeho zrychlením (\vec a) a setrvačností tělesa vyjádřenou jeho hmotností (m).
\vec F=m\cdot \vec a
Rovnice napsaná bez znázornění vektorových veličin (F=m\cdot a) je také častá, zejména když není směr zrychlení důležitý (např. vše probíhá na přímce).
- Těleso o hmotnosti 1 kg se pohybuje se zrychlením 1 m/s² → síla 1 N.
- Láhev limonády (2 kg) padá se zrychlením asi 10 m/s² → síla 20 N.
- Karta BANGu (0,001 g) klouže po stole a brzdí se zrychlením 2 m/s² → síla 0,002 N.
Jiné tvary
Pomocí matematických úprav můžeme dojít k dalším tvarům:
\vec a=\frac{\vec F}{m}
Tento tvar je fyzikálně asi nejlogičtější, protože zrychlení, které je z našeho pohledu následek (levá strana rovnice), je důsledkem příčin tohoto pohybu (přítomnost sil \vec F, setrvačnost tělesa kvůli hmotnosti m).
- Sáně s dítětem (10 kg) táhne výsledná síla 5 N → Síla způsobí zrychlení saní 0,5 m/s².
- Auto (1500 kg) brzdí s výslednou silou 6000 N → Zrychlení (resp. zpomalení) auta bude 4 m/s².
m=\frac{F}{a}
Protože je hmotnost skalár, je podílem velikostí obou vektorů, což můžeme zapsat právě jako \frac{F}{a} (bez šipek) nebo uzavřením vektorů do svislých čar m=\frac{\lvert\vec F\rvert}{\lvert\vec a\rvert}.
- Vláček pohání výsledná síla o velikosti 0,3 N a pohybuje se se zrychlením 1,5 m/s². → Musí mít hmotnost 0,2 kg.
Zajímavosti
Protože \vec F i \vec a jsou vektory a m je jen skalár (číslo) směřují zrychlení i výsledná síla stejným směrem.
Zákon síly není definicí síly, protože o ní nic konkrétního neříká (odkud se vzala, jaká je, …).
Původní Newtonova formulace
Mutationem motus proportionalem esse vi motrici impressae et fieri secundam lineam rectam qua vis illa imprimitur.
Zákon akce a reakce
Zákon akce a reakce, neboli třetí Newtonův zákon popisuje vzájemné působení (interakci) dvou těles.
Definice
Každé působení prvního tělesa na druhé (silou \vec F_{12}), neboli akce, vyvolává stejně velkou, opačně orientovanou reakci působení druhého tělesa na první (\vec F_{21}).
Matematicky to můžeme vyjádřit jako \vec F_{12}=-\vec F_{21}.
Taková dvojice sil vypadá následovně:
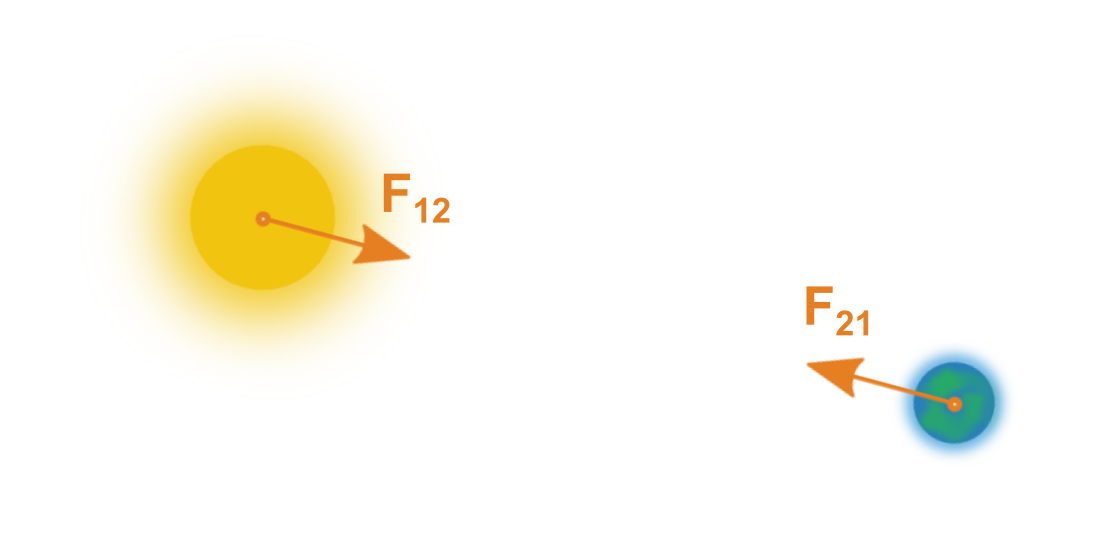
- Země přitahuje Slunce stejně velkou silou jako Slunce přitahuje Zemi (jen je ta síla na obrovskou hmotnost Slunce relativně slabá).
- Tlačíme nepojízdné auto silou F. Auto zase otlačuje naše ruce silou -F
- Raketoplán urychluje hořící palivo z trysek dozadu. Toto palivo jej tedy tlačí kupředu.
- Když chceme udělat krok, třením podrážky odstrkujeme zeměkouli dozadu. Na oplátku na nás země pusobí silou směrem vpřed, která naše tělo rozpohybuje.
- Když narazí kulečníková koule do druhé, zapůsobí na ni silou a rozpohybuje ji. Ale sama přitom svůj pohyb změní. Ta druhá koule tedy musela zapůsobit zase na ni.
Vlastnosti
Ačkoliv jsou síly opačně orientované a stejně velké, jejich výslednice není nulová. Působí totiž každá na jiné těleso, nemůžeme je tedy sčítat.
Akce i reakce na ni probíhají okamžitě (alespoň v Newtonovském pojetí času), společně vznikají a společně zanikají. Nelze tedy určit, která je první.
- Když se opřeme
Zajímavosti
- „Actioni contrariam semper et aequalem esse reactionem; sive: corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.“ (Newtonova formulace)
- Protože jsou akce i reakce současné a nerozlišitelné, dalo by se o tomto zákonu s trochou drzosti mluvit spíše jako o zákonu INTERakce.
- Důsledkem zákona akce a reakce je i zákon zachování hybnosti.
Síly, které pozorujeme kolem nás, mají různý původ a hodí se umět je rozlišovat.
V mechanice se setkáme s kontaktními silami, které se objeví jen při kontaktu dvou těles/látek. Dělíme je na normálové (kolmo k povrchu v místě kontaktu) a tečné (podél). Mezi normálové patří zejména síly tahu a tlaku (víceméně všechny spoje a kontaktní plochy těles). Tečné jsou pak různé síly odporu prostředí během pohybu (třecí síla, odpor větru, …), bez kterých bychom naše auta nemohli ani rozjet, ani zastavit.
Na dálku (bezdotykově) pak působí gravitační síla mířící do těžiště druhého tělesa (např. do středu Země). Mimo klasickou mechaniku se setkáme s dalšími dalekodosahovými bezdotykovými silami – elektrickou mezi elektrickými náboji (např. elektrostatickou na nabitých baloncích) nebo magnetickou mezi magnety (objevuje se ale i tam, kde proudí elektrický proud).
Speciální název mají i některé součty sil. Například pod vodou je na těleso zespodu větší tlaková síla než shora. Součet tlakových sil na toto těleso, jej tedy nadlehčuje – vztlaková síla. Zemská přitažlivost je u nás zase zmenšována odstředivou silou rotace Země. Součet, který vnímáme, tedy nazýváme tíhovou silou.
Zajímavosti
Ve skutečnosti jsou úplně všechny z výše zmíněných sil kromě gravitačních elektromagnetického původu. Na mikroskopické úrovni je totiž zprostředkují atomy. Například když proti sobě tlačíme dva materiály, je tlaková síla jen projevem elektrostatického odpuzování krajních atomů.Newtonův gravitační zákon
Gravitační působení mezi dvěma tělesy popisuje podle Newtona gravitační síla F_g:
F_g=G\frac{m_1\cdot m_2}{r^2}
kde G je gravitační konstanta (často se také značí \kappa), m_1 a m_2 jsou hmotnosti těles a r je vzdálenost jejich středů hmotnosti (těžišť). Používáme ji většinou ve vesmíru, kde jsou vzdálenosti mnohem větší než rozměry těles, takže často neuděláme velkou chybu když za r bereme vzdálenost mezi předměty.
Gravitační síly jsou vždy přitažlivé a jde o síly akce a reakce (vždy vznikají dvě, obě stejně velké opačně orientované).
Definujeme i gravitační zrychlení a_g. Na rozdíl od gravitační síly není závislé na obou hmotnostech – např. zrychlení způsobené tělesem 2 je podle druhého Newtonova zákona a_g=F_g/m_1.
Tedy po dosazení do F_g je a_g=\kappa\frac{m_2}{r^2}.
Protože stejně velké gravitační síly těles 1 a 2 dělíme různými hmotnostmi, nejsou gravitační zrychlení stejně velká.
Gravitační konstanta \kappa má hodnotu 6,67⋅10⁻¹¹ m³s⁻²kg⁻¹.
Příklad: člověk a Země
- Máme zjistit podle F_g=\kappa\frac{m_1\cdot m_2}{r^2} sílu mezi člověkem stojícím na zemi a jeho planetou.
- m_1 je asi 100 kg, tedy 10² kg
- m_2 je asi 6⋅10²⁴ kg
- r je přibližně poloměr Země 6378 km, zaokrouhleně 6,3 milionů metrů, tedy 6,3⋅10⁶ m
- Zde bychom tedy r jako vzdálenost těles (0 m) brát nemohli.
- Dosadíme spolu s konstantou \kappa do vzorce:
- F_g=6,67⋅10⁻¹¹ \frac{10²\cdot 6⋅10²⁴}{6{,}3⋅10⁶⋅6{,}3⋅10⁶}\,\mathrm{N}=\frac{6,67⋅6}{6{,}3⋅6{,}3}10³\,\mathrm{N}\approx10³\,\mathrm{N}
- Na 100kg člověka tedy působí asi 1000 N gravitační síla.
- To sedí i na jednodušší tíhovou sílu F_G=m_1\cdot g (u země je g\approx 10\,\mathrm{m⋅s⁻²})
Gravitační vs. tíhová síla a tíha
Tíhová síla
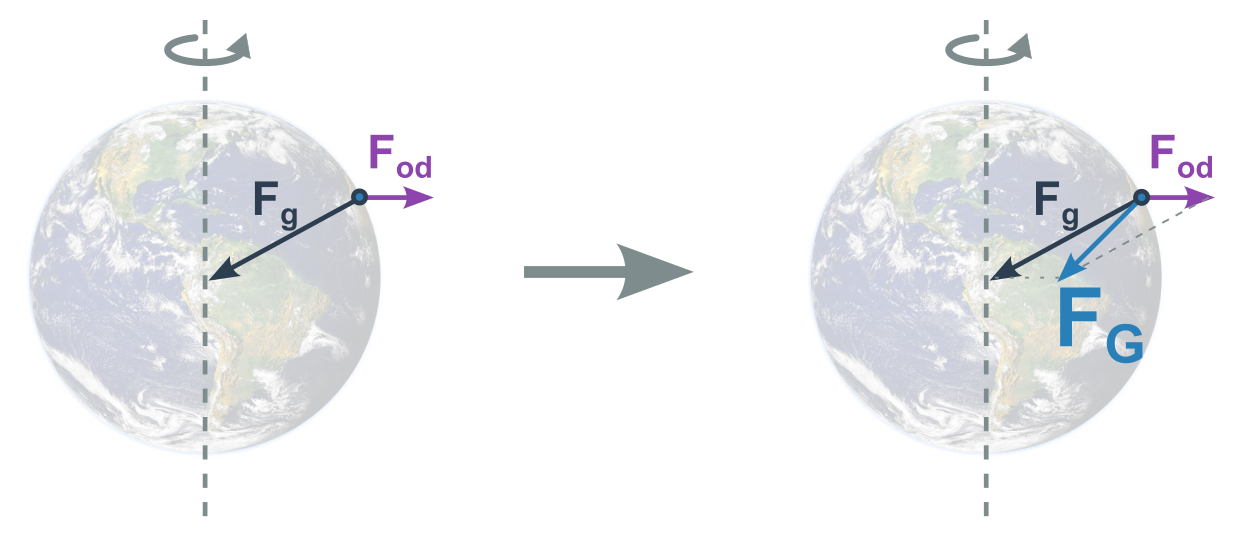
Pro popis dynamiky pohybu na zemi a u země nepoužíváme přímo gravitační sílu F_g, protože to úplně nevychází. Nacházíme se totiž na rotující (Země)kouli a v naší vztažné soustavě musíme započítat odstředivou sílu.
Tento součet (gravitační a odstředivé síly) označujeme jako tíhovou sílu F_G. Podobně máme místo gravitačního zrychlení a_g tíhové zrychlení g. Působištěm tíhové síly je těžiště tělesa (stejně jako u gravitační síly).
Tíha
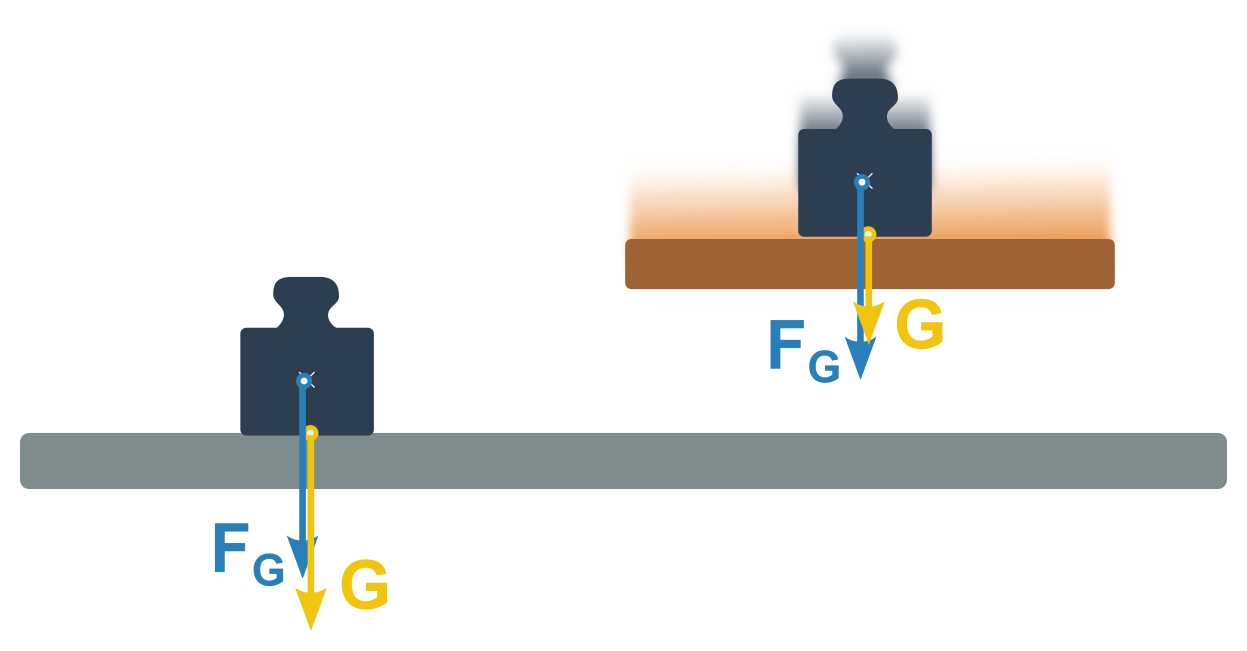
Ani tíhová síla není ale vždy rovna velikosti síly, jakou tlačí např. naše nohy na podlahu pod námi.
Proto zavádíme tíhu G. Jde v podstatě o tlakovou sílu na podložku (způsobenou tíhovou silou). Působištěm tíhy je místo kontaktu s podložkou. Rozdíl ve velikosti mezi tíhou a tíhovou silou poznáme u soustav zrychlujících ve svislém směru.
Příklad : Výtah
- Ve výtahu na nás působí stále stejná tíhová síla F_G.
- Když se ale výtah rozjíždí nahoru, cítíme se těžší – je totiž větší naše tíha G.
- Při rozjezdu směrem dolů je naše tíha naopak menší.
- kdyby výtah začal padat volným pádem, bude naše tíha dokonce nulová. Ale to nechceme…
Tlak a tlaková síla
Definice
Tlak (značíme p) je veličina popisující deformační (ne pohybové) účinky síly na těleso. Je definován pomocí tlakové síly \vec F působící kolmo na určitou plochu S.
p = \frac{F}{S}
Úpravou rovnic (nebo pomocí vztahového trojúhelníku níže) můžeme odvodit další vztahy:
F = p \cdot S
S = \frac{F}{p}
Jednotky
Jednotkou je (jak ze vztahu p = F/S vyplývá) newton na metr čtvereční (N/m²). Tato jednotka dostala také vlastní název – pascal.
Typicky se setkáváme se silami v jednotkách až stovkách newtonů působícími na plochy mnohem menší než je metr čtvereční. Proto se kolem nás setkáváme nejčastěji s tlaky v tisících, ne-li milionech pascalů.
Vtip o jednotkách
Archimedes, Pascal a Newton hrají na schovávanou. Archimedes piká. Pascal se rychle schová do křoví.
Newton se vůbec neschovává, jen do hlíny klackem namaluje čtverec metr krát metr a postaví se do něj.
Archimedes dopiká, okamžitě uvidí Newtona a volá: „Deset dvacet Newton!“
Newton v klidu řekne: „Nene. Newton na metr čtvereční je přece pascal!“
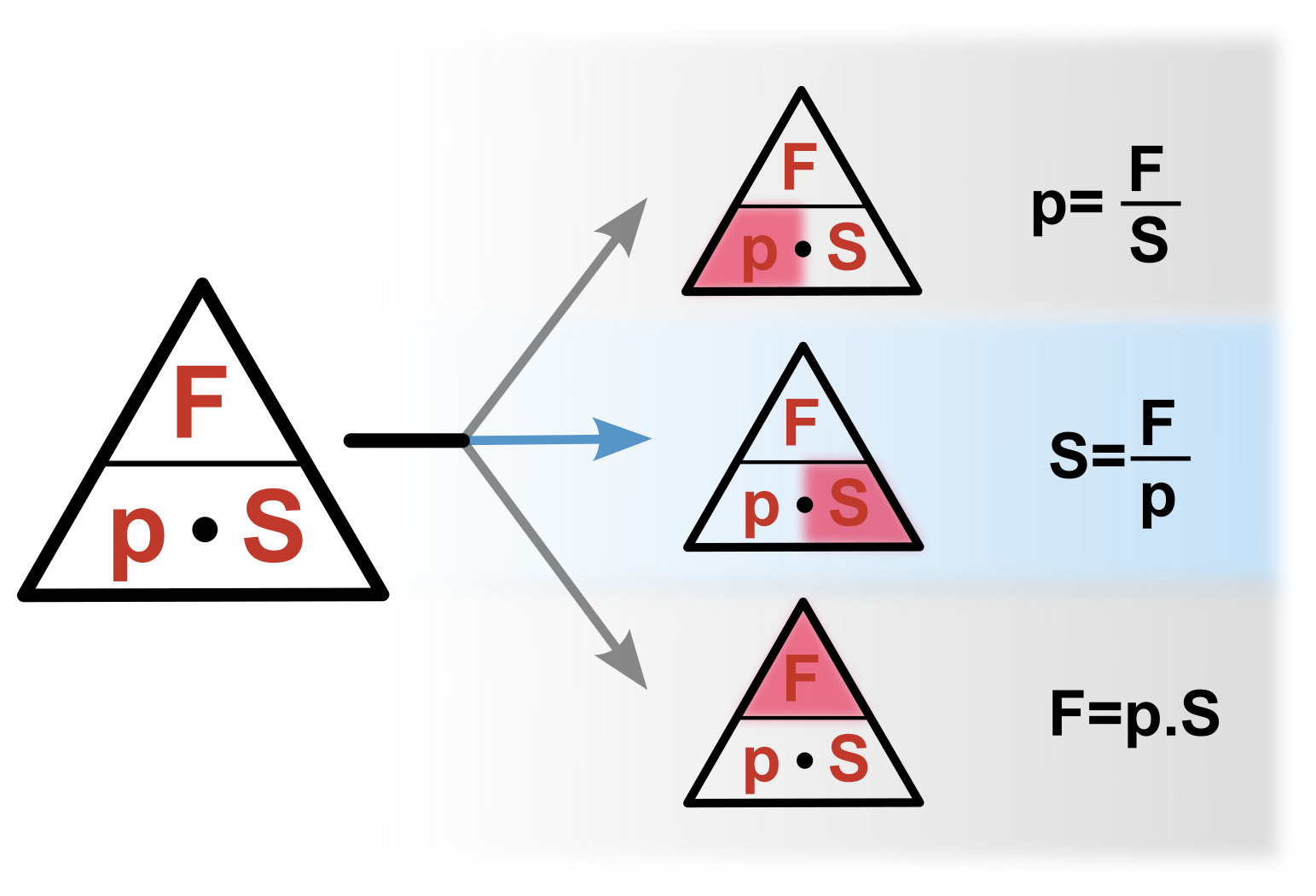
Vztahový trojúhelník
Pro získání vzorce pro libovolnou veličinu p, F, S můžeme použít vztahový trojúhelník (pyramidu). Více o tom jak se vytváří a funguje najdete zde.
Zajímavost: Jednotka SI
Jednotka pascal je v soustavě SI teprve od roku 1971.
Poznámka: Ne vždy lze jednoduše znázornit tlakovou sílu s působištěm v místě doteku (např. více končetin). Proto v některých příkladech používáme k ilustraci i tíhovou sílu s působištěm v těžišti. Má totiž stejnou velikost jako tlaková síla, kterou vyvolává.
NahoruSmykové tření: základy
Mezi dvěma tělesy, která jsou v kontaktu, působí různé síly. Jednou skupinou těchto sil je působení mezi jejich povrchy, pokud jsou v přímém kontaktu (doteku).
Když se dvě tělesa po sobě sunou dochází ke smykovému tření (sunutí=smýkání). Vzniká tzv. třecí síla namířená proti směru pohybu (nebo proti směru, ve kterém se o pohyb snažíme). Záleží na tlakové síle a vlastnostech povrchů obou materiálů (hlavně nerovnosti a jak do sebe zapadají).
Jak po sobě umí daná dvojice materiálů klouzat vyjadřuje experimentální konstanta, tzv. koeficient smykového tření (čím nižší, tím lepší klouzání).
| Materiály | Koeficient |
|---|---|
| ocelový nůž brusle a led | 0,03 |
| hladká ocel a mosaz (naolejované) | 0,11 |
| cihla a suché dřevo | 0,60 |
| pneumatika a suchý asfalt | 0,72 |
| guma a guma | 1,16 |
| (většinou se f pohybuje v rozmezí 0 až 1) |
Smykové tření dělíme na klidové (statické) a smykové tření v pohybu (dynamické).
Klidové tření
Probíhá, dokud jsou tělesa vzájemně v klidu a ještě nedochází ke smýkání (i když se jej nějaká síla snaží vyvolat). Třecí síla je tím, co rozpohybování brání. Například jde o:
- auto zabrzděné v kopci
- sešit ležící na křivém stole
- skříň, kterou se snažíme posunout, ale nemůžeme s ní ani hnout
Třecí síla je pak rovna silám, které se pokoušejí vyvolat vzájemný pohyb. Má ale svoji horní hranici. Pokud je překročena, tělesa se začnou smýkat a přesouváme se do kategorie smykového tření v pohybu.
Smykové tření v pohybu
Setkáme se s ním, když se po sobě tělesa pohybují. Funguje jako brzda působící proti směru pohybu. Jde například o:
- dítě klouzající po skluzavce
- tužku píšící na papír
- koleno drásající se o asfalt
- nebo i ten sešit, když se jej pokusíme položit na příliš nakloněný povrch
Smykové tření: se vzorci a třecí silou
Mezi dvěma tělesy, která jsou v kontaktu, působí různé síly. Jednou skupinou těchto sil je působení mezi jejich povrchy, pokud jsou v přímém kontaktu (doteku).
Tyto síly jsou mikroskopické (slabé vazby mezi nejbližšími atomy) i makroskopické (nerovnosti které do sebe zapadají) a mají většinou hlavní vliv na pohyb jednoho tělesa po druhém. Pokud se tělesa po sobě sunou (nevalí), říkáme účinkům takových sil smykové tření (sunutí=smýkání).
Sílu, která směřuje proti směru pohybu (nebo proti směru, ve kterém se o pohyb snažíme), nazýváme třecí silou F_t. Tato třecí síla záleží na tlakové síle F_N, kterou proti sobě povrchy působí, a na tom, jak dobře po sobě povrchy umí klouzat. To pro danou dvojici materiálů vyjadřuje experimentální konstanta koeficientu smykového tření f.
| Materiály | Koeficient f |
|---|---|
| ocelový nůž brusle a led | 0,03 |
| hladká ocel a mosaz (naolejované) | 0,11 |
| cihla a suché dřevo | 0,60 |
| pneumatika a suchý asfalt | 0,72 |
| guma a guma | 1,16 |
| (většinou se f pohybuje v rozmezí 0 až 1) |
Smykové tření dělíme na klidové (statické) a smykové tření v pohybu (dynamické).
Klidové tření
Probíhá, dokud ještě nedochází ke smýkání, i když se jej nějaká síla snaží vyvolat. Například jde o:
- auto zabrzděné v kopci
- sešit ležící na křivém stole
- skříň, kterou se snažíme posunout, ale nemůžeme s ní ani hnout
Třecí síla je pak stejně velká jako výslednice sil, které se pokoušejí vyvolat pohyb. Maximální klidová třecí síla je vyjádřena z F_N a f jako
F_t=f\cdot F_N
pokud tuto hodnotu ostatní síly překonají, těleso se rozpohybuje.
Smykové tření v pohybu
Funguje jako brzda působící proti směru pohybu. Jde například o:
- dítě klouzající po skluzavce
- tužku píšící na papír
- koleno drásající se o asfalt
- nebo i ten sešit, když se jej pokusíme položit na příliš nakloněný povrch
Tření v pohybu je o něco slabší, než maximální klidové tření. Výpočet F_t=f\cdot F_N platí i zde, ale koeficient f je v pohybu nižší. Např. pneumatika ve smyku nebude mít f=0{,}72 ale jen f=0{,}65. Často se tedy i označují odlišně – například f_0 v klidu a f v pohybu.
Zajímavosti
- Nižší f v pohybu můžeme vysvětlit tak, že povrchy nemají dost času do sebe co nejlépe zapadnout.
- Protože je pohybové tření menší než to klidové, znamená to, že kvádr, který jednou po nakloněné rovině rozjede, se už nezastaví. Až dole.
Hybnost je vektorová fyzikální veličina, kterou značíme \vec p (její velikost je p) a která je definovaná poměrně jednoduše – jako součin rychlosti tělesa a jeho hmotnosti. Jednotkou je tedy součin jednotek obou veličin – kg⋅m/s.

Matematicky hybnost zapisujeme takto:
\vec p=m\cdot \vec v.
Protože jde o vektorovou veličinu, musíme za změnu hybnosti považovat nejen její zmenšení/zvětšení, ale i změnu jejího směru (tedy směru rychlosti).
Na první pohled je zavedení takové veličiny zbytečné (pouze násobek rychlosti). Je ale důležitá pro popis soustavy více těles. Můžeme určit celkovou hybnost soustavy – součet hybností jednotlivých těles (vektorový součet, viz obrázek).
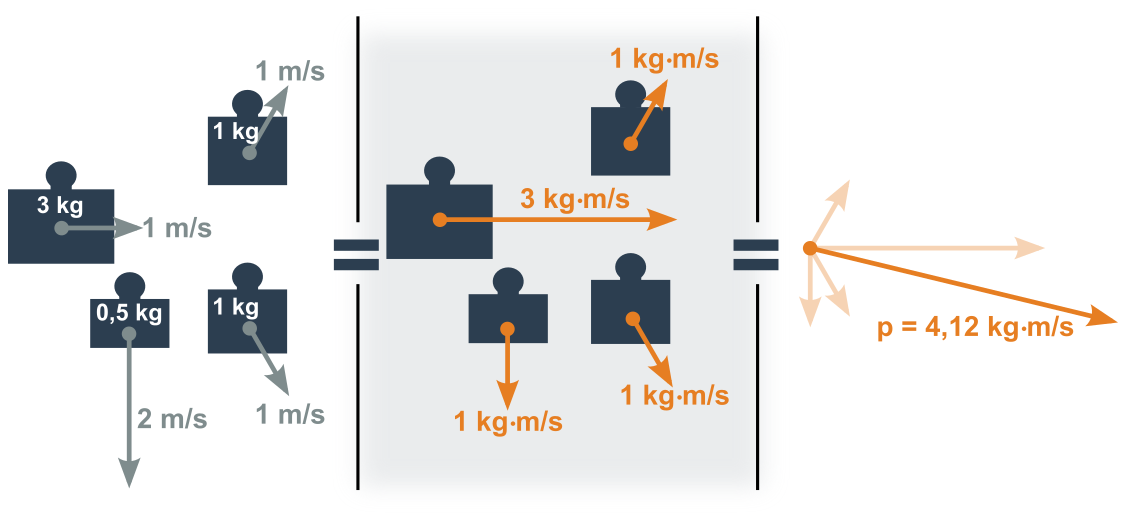
Matematicky zapsáno:
\vec p = \vec p_1+\vec p_2+\vec p_3+\cdots
Celková hybnost těles izolované soustavy se nemění, ať se mezi nimi děje cokoliv (srážky, tření, gravitační přitahování, magnetické síly, …). Říká se tomu zákon zachování hybnosti.
Zajímavosti
- Na principu zákona zachování hybnosti jsou založeny sporty jako kulečník nebo curling. Také tím vysvětlíme zpětný ráz při výstřelu z děla nebo explozi rachejtle na nočním nebi.
Moment síly
Působení síly na těleso může být posuvné a otáčivé. Zatímco posuvné účinky síly (\vec F) popisuje druhý Newtonův zákon, otáčivé účinky sil vyjadřuje tzv. moment síly.
Když fotbalista kopne do míče, míč se nejen rozletí ale také (často) začne rotovat.
Moment síly (značíme \vec M) je vektorová veličina. Čím má moment síly větší velikost, tím rychleji roztáčí těleso. Základní jednotkou momentu síly je jeden newtonmetr (Nm).
Velikost
Velikost momentu síly se počítá jako součin velikosti síly F a ramene síly r_\perp.
M=r_\perp \cdot F
Rameno síly není vždy vzdálenost síly od osy otáčení. Je to vlastně kolmá vzdálenost osy otáčení od přímky, ve které leží síla F. Lépe je to pochopitelné z obrázku 1. Zde jej značíme jako r_\perp (a vzdálenost od osy jako obyčejné r). Je to proto, že se v různých učebnicích značení liší (r, d, a, …).

Případně lze použít i ekvivalentního vztahu M=r F \sin (\alpha), kde \alpha je úhel mezi \vec F a \vec r.
Směr
Moment síly je kolmý na sílu i na rameno síly. Jeho směr se dá zjistit pomocí pravidla pravé ruky.
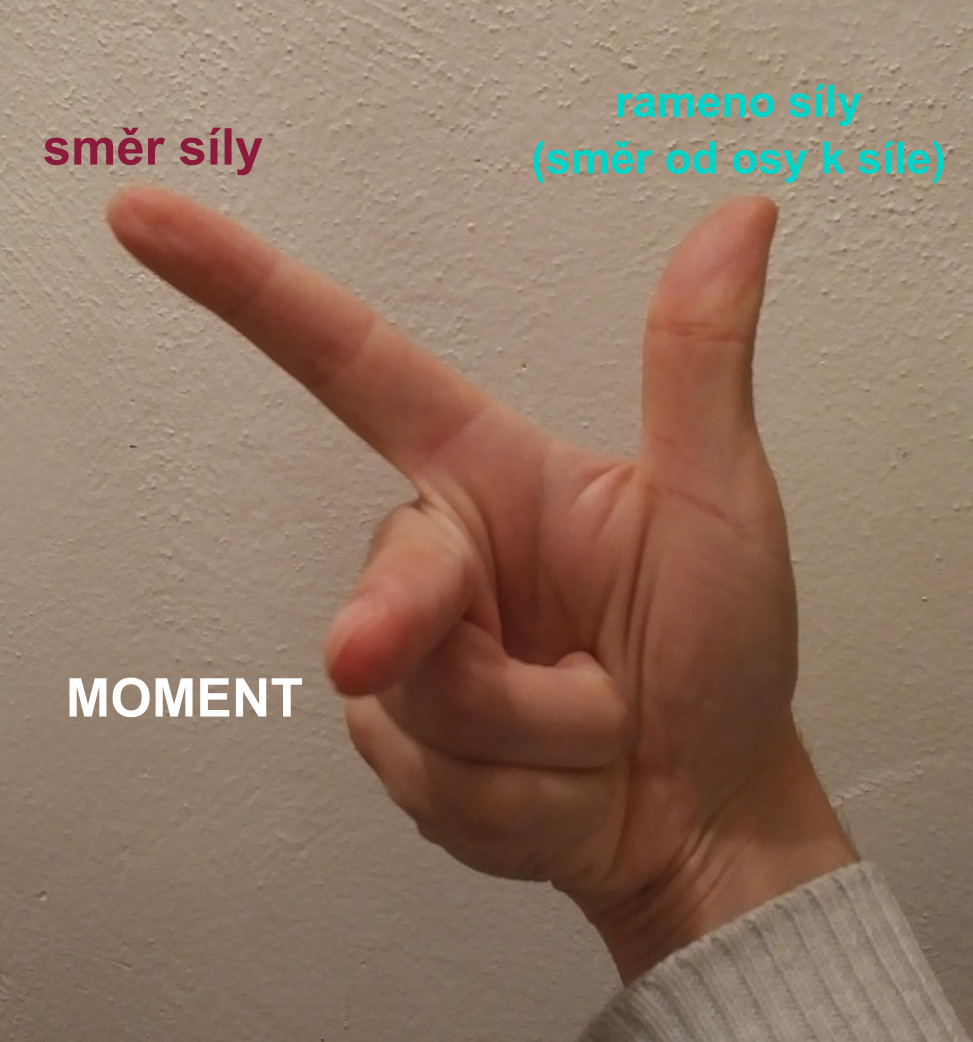
Protože je moment síly závislý na ose otáčení, znamená to, že jedna síla může mít různé momenty vůči různým osám (například vůči přednímu a zadnímu kolu bicyklu).
Nahoru
