Pokud se rychlost pohybu mění, charakterizuje tyto změny veličina jménem zrychlení. Značíme jej a a je to změna rychlosti za změnu času.
a=\frac{\Delta v}{ \Delta t }
- Rychlost lodi vzrostla o 6 m/s během 3 s. Zrychlení bylo 2 m/s².
Jednotkou zrychlení je \mathrm{m/s^2}.
Zejména v kinematice můžeme zrychlení brát jako změnu velikosti rychlosti. Pokud je stále stejné, jde o pohyb rovnoměrně zrychlený nebo pohyb rovnoměrně zpomalený.
Pro rychlost rovnoměrně zrychleného pohybu platí:
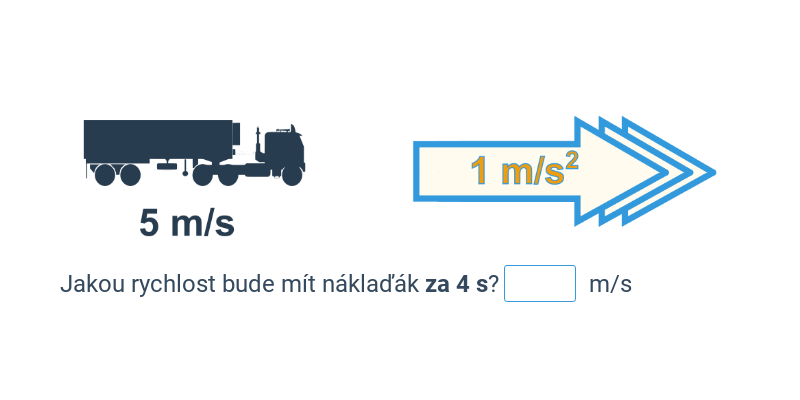
v=v_0+a\cdot t nebo jednodušeji v=a\cdot t (pokud je počáteční rychlost v_0 nulová)
Vztah pro dráhu je pak:
s=v_0t+\frac{1}{2}a t^2 nebo jednodušeji s=\frac{1}{2}a t^2 (pokud je počáteční rychlost v_0 nulová)
V případě rovnoměrně zpomaleného pohybu (rychlost se rovnoměrně snižuje), používáme obvykle vztahy v=v_0-a\cdot t pro rychlost a s=v_0t-\frac{1}{2}a t^2 pro dráhu.
Zjednodušené vztahy (v_0=0) v tomto případě nemají smysl, protože musíme mít z čeho zpomalovat.
Zpomalení a záporné zrychlení
Je i alternativa používat pro zpomalený pohyb stejné vztahy jako pro pohyb zrychlený a dosazovat záporné hodnoty zrychlení a. V následujících cvičeních ale není použita.
Přesnější definice zrychlení je změna vektoru rychlosti za změnu času.
\vec a=\frac{\Delta \vec v}{ \Delta \vec t }
Zrychlení je podle této definice nenulové i u rovnoměrného pohybu po kružnici a každého křivočarého pohybu (mění se směr vektoru rychlosti).