Výpis souhrnů
Kinematika (popis pohybu)
Podtémata
- Kinematika (popis pohybu)
- Kinematika: základní pojmy
- Rychlost, dráha, čas
- Rychlost, dráha, čas: vzorce
- Rychlost, dráha, čas: pohyb tělesa
- Rychlost, dráha, čas: vzájemný pohyb těles
- Rovnoměrný a nerovnoměrný pohyb
- Zrychlení
- Dráha zrychleného pohybu
- Grafy pohybu
- Typy grafů pohybu
- Grafy polohy/dráhy: základy
- Grafy polohy/dráhy: odečítání údajů
- Grafy rychlosti: základy
- Grafy rychlosti: odečítání údajů
- Výpočty rychlosti a dráhy z grafů
- Vrhy a pády
- Poznávání vrhů
- Vlastnosti vrhů
- Volný pád
- Pohyb po kružnici
Kinematika (popis pohybu)
Je částí mechaniky, jejímž úkolem je popsat pohyb. Popisovat můžeme pohyb jednotlivých objektů, pohyb souboru objektů, pohyb tekutin a tak dále. V první části se ovšem převážně zaměřujeme na popis pohybu pevných těles.
Kinematika se nesnaží pohyb vysvětlit (proč se něco hýbe), to je podstatou dynamiky. Kinematika se jen ptá, jak se objekty pohybují prostorem:
Rovně?
Do zatáčky?
Stále stejně?
Čím dál tím rychleji?
Kinematika: základní pojmy
V mechanice se pohybují především různé objekty, tzv. tělesa. Často je zjednodušujeme na hmotné body (neuvažujeme rozměry a rotaci tělesa, jen hmotnost).

Křivku vykreslující kudy pohyb procházel nazýváme trajektorie. Její délka se nazývá dráha.
Popisovat pohyb můžeme z několika úhlů pohledu:
Jak se na pohyb díváme?
Pohyb musíme popisovat vůči něčemu. Proto zavádíme vztažné soustavy, tedy body vůči kterým poměřujeme svět a změny v něm. Obvykle je vztažná soustava určena počátečním bodem a souřadnicovými osami. Z různých vztažných soustav bude stejný pohyb vypadat jinak:

Speciálním případem je inerciální vztažná soustava, která nezrychluje a nezatáčí (nepociťujeme v ní setrvačné síly jako např. v brzdícím autobuse). Inerciální soustavy se vůči sobě pohybují stále stejným směrem a stejně rychle.
Jak pohyb vypadá?
Podle tvaru trajektorie rozdělujeme pohyby na přímočaré (pohybuje se stále rovně) a křivočaré (zatáčí).

U těles také rozlišujeme, jestli se někam posouvá, nebo se točí. Nebo obojí. Porovnáním trajektorií jednotlivých bodů tělesa tedy rozlišíme pohyb posuvný (translační) a otáčivý (rotační), případně složený.

Jak pohyb probíhá?
Z tvaru trajektorie zjistíme kudy se někdo pohyboval, ale už ne jak rychle. Stejnou zatáčku na polní cestě může opsat šnek i auto. Veličinou, která tyto pohyby odlišuje, je rychlost. Značíme ji v a je rovna dráze dělené časem t. Je buď průměrná (tedy podíl dráhy a času za nějakou dlouhou dobu) nebo okamžitá (změny dráhy za malou změnu času).
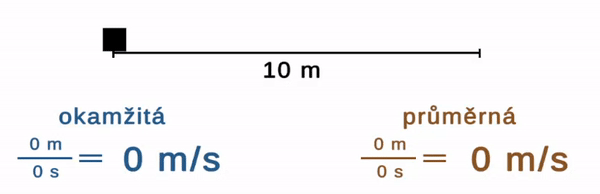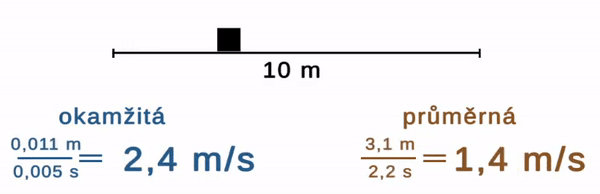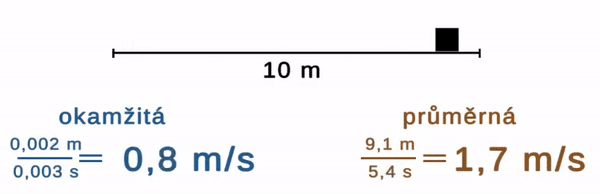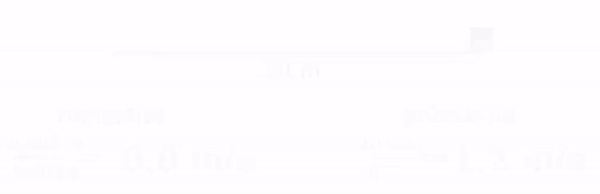
Pokud je rychlost stále stejně velká, mluvíme o rovnoměrném pohybu. Pokud se mění, jde o pohyb nerovnoměrný.

Jaký je tedy pohyb?
Výše zmíněné vlastnosti pohybu se různě kombinují, můžeme mít posuvný pohyb rovnoměrný a přímočarý, posuvný pohyb nerovnoměrný a přímočarý, rovnoměrný otáčivý pohyb a tak dále.
Zajímavosti
Inerciální soustava ve skutečnosti prakticky neexistuje. Vždyť i Sluneční soustava obíhá okolo galaktického jádra (a nepohybuje se tedy rovnoměrně přímočaře). Jsou jen soustavy, které jsou blíže k tomuto ideálu než jiné.
Rychlost, dráha, čas
Vztah mezi rovnoměrnou (nebo alespoň průměrnou) rychlostí v drahou s a časem pohybu t popisují vzorce:
v=\frac{s}{t}
s=v\cdot t
t=\frac{s}{v}
V jednoduchých případech pouze určíme správný vzorec a dosadíme.
U mnoha pohybů těles ovšem před dosazením musíme udělat něco navíc, např. převést správně jednotky nebo určit s ze změny poloh.
Konečně můžeme pomocí těchto vztahů také řešit vzájemný pohyb více těles.
Vztahový trojúhelník (pyramida)
Pokud známe nějaký vzorec typu \bf{A=B\cdot C} nebo \bf{A=B/C} (například v=s/t) můžeme pomocí jednoduché pomůcky zjistit, jak vypadají vzorce pro \bf{B} a pro \bf{C}.
- Nakreslíme si trojúhelníkovou pyramidu (zatím prázdnou).
- Zakreslíme do ní pravou stranu rovnice (naše s/t), tak aby vypadala graficky stejně jako ve vzorci (dělení jako zlomek nad sebou, případně násobení vedle sebe v dolním patře).
- Na zbývající místo doplníme levou stranu vzorce.

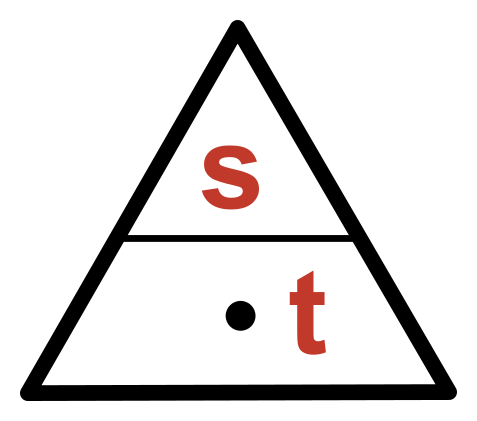
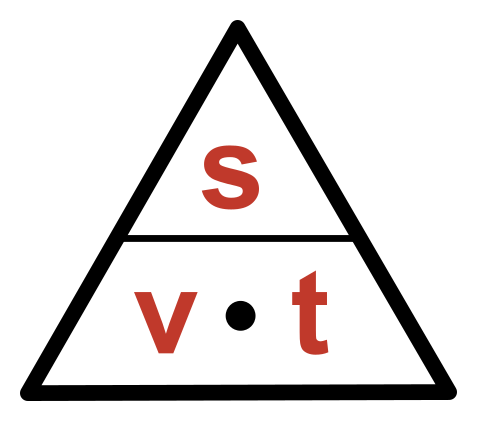
- Nyní stačí pro výpočet jakékoliv veličiny zakrýt tuto veličinu prstem a podívat se jak vypadají ostatní nezakryté.
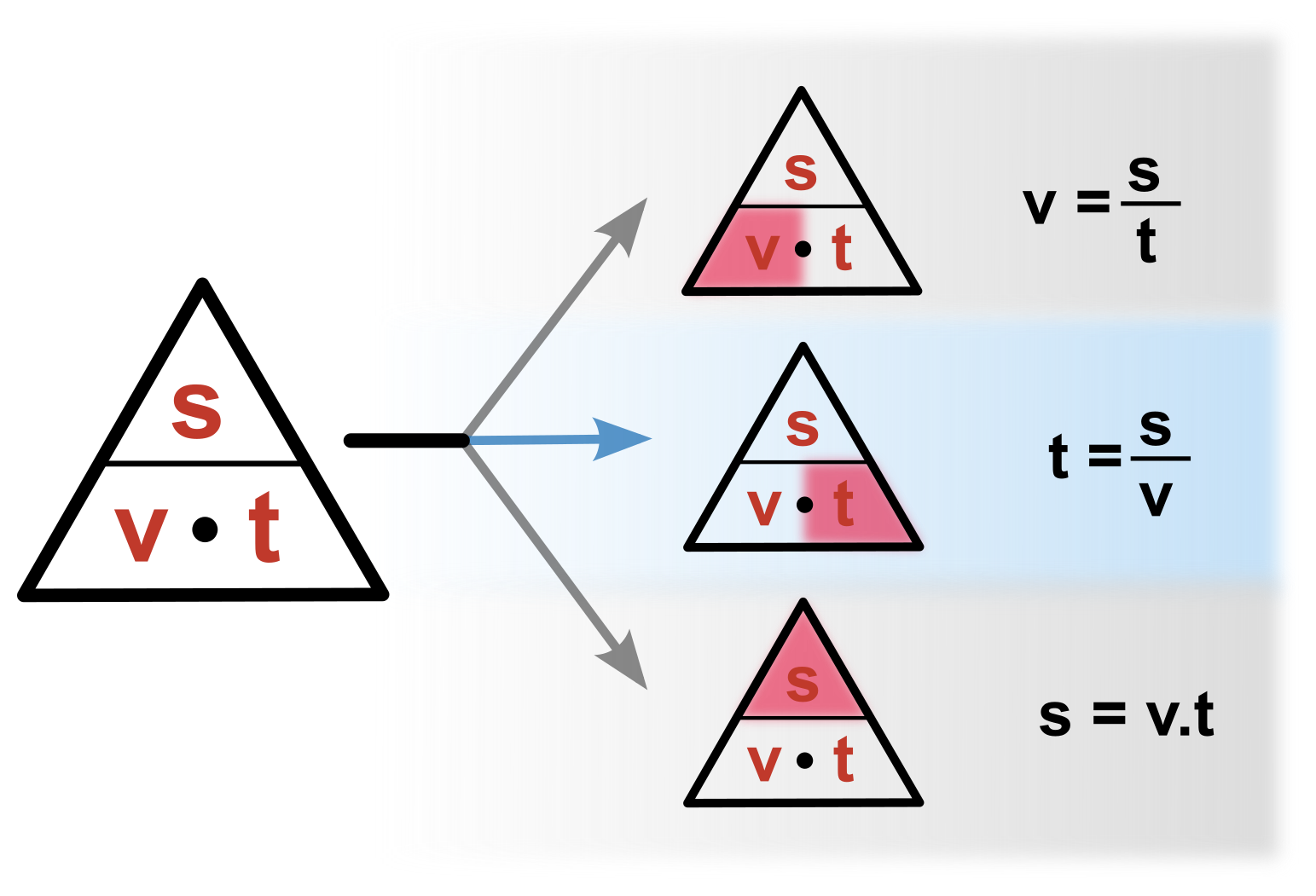
Rychlost, dráha, čas: vzorce
Definice rychlosti v je dráha s za čas t. Matematicky zapsáno je to
v=\frac{s}{t}
Jde vlastně o rychlost průměrnou, ale v případě rovnoměrného pohybu i o okamžitou rychlost po celou dobu pohybu.
Příklad: Rychlost auta
- Auto ujelo 200 km za 4 h. Jakou udržovalo rychlost?
- Hledáme v a známe s a t. Použijeme tedy vzorec v=\frac{s}{t}
- Dosadíme do něj za s a t.
- v=\frac{200}{4}\,\mathrm {km/h}=50\,\mathrm {km/h}
- Auto udržovalo rychlost 50 km/h.
Můžeme počítat i s a t (vždy když známe zbývající dvě veličiny). Matematickou úpravou, resp. použitím vztahového trojúhelníku jsme odvodili vztahy pro dráhu
s=v\cdot t
Příklad: Dráha Tarzana
- Tarzan na liáně letí rychlostí 12 m/s po dobu 5 s než se rozplácne o strom. Jakou dráhu uletěl?
- Hledáme s a známe v a t. Použijeme tedy vzorec s=v\cdot t.
- Dosadíme za v a t.
- s=12 \cdot 5\,\mathrm m=60\,\mathrm m
- Tarzan se rozplácl po 60 m.
a pro čas
t=\frac{s}{v}.
Příklad: Letové hodiny stíhačky
- Stíhačka přeletěla 800 km rychlostí 1600 km/h. Jak dlouho letěla?
- Hledáme t a známe s a v. Použijeme tedy vzorec t=\frac{s}{v}
- Dosadíme do něj za s a v.
- t=\frac{800}{1600}\,\mathrm h=0{,}5\,\mathrm h
- Stíhačka letěla půl hodiny.
Rychlost, dráha, čas: pohyb tělesa
Ne vždy můžeme ihned dosadit do vzorců jako s=v\cdot t. Musíme totiž nejprve vyřešit drobné komplikace:
- Jednotky nesedí. Musíme převést na stejné jednotky, nebo alespoň tak abychom nekombinovali různé časové škály (např km/h se sekundami)
Autobus
- Autobus jel 15 minut rychlostí 40 km/h. Kolik toho ujel?
- V jednotce rychlosti jsou hodiny zatímco čas je v minutách. Musíme tedy převádět.
- Mohli bychom převádět na m/s a sekundy, ale bylo by to pracné.
- Lepší je převést čas na hodiny (výsledek vyjde v km).
- 15 minut → 0,25 h
- Konečně můžeme dosadit do s=v\cdot t.
- s=40\cdot 0{,}25 \,\mathrm{km} = 10\,\mathrm{km}
- Dráhy/časy složené z více částí. Celková dráha pohybu s je prostě součtem drah všech úseků s=s_1+s_2+\cdots. Totéž platí pro čas t=t_1+t_2+\cdots.
Triatlon
- Triatlonista zvládl závod za 2h. Přitom ujel 40 km na kole, 10 km běžel a 1,5 km plaval. Jakou měl průměrnou rychlost během celého závodu?
- Použijeme vzorec v=\frac{s}{t}, ale přímo známe jen čas t. Potřebujeme s.
- Celková dráha s je podle s=s_1+s_2+s_3
- Číselně s=40+10+1{,}5\,\mathrm {km}= 51{,}5\,\mathrm {km}.
- Už můžeme dosazovat v=\frac{51{,}5}{2}\,\mathrm {km/h}=25{,}75\,\mathrm {km/h}
Pro rychlost to ale neplatí! Průměrná rychlost více úseků dohromady se musí počítat jako v=\frac{s_1+s_2+\cdots}{t_1+t_2+\cdots}.
- Místo dráhy/času známe jen hodnoty na začátku a na konci. Neznáme dráhu přímo, ale známe polohy na trati na začátku a na konci pohybu. Podobně může být potřeba určit dobu pohybu t jako rozdíl časů (na hodinách) v okamžiku startu a cíle.
Sjezdy na dálnici
- Na dálnici jsme najeli nájezdem na 20. km a opustili ji sjezdem na 200. km. Jak dlouho jsme na ní strávili s rychlostí 90 km/h?
- Hledáme t. Přímo známe ale jen v.
- Dráhu s musíme určit jako rozdíl poloh na začátku a na konci.
- s=200-20\,\mathrm{km}=180\,\mathrm{km}
- Teprve nyní můžeme dosadit do t=\frac{s}{v}.
- t=\frac{180}{90}\,\mathrm{h}=2\,\mathrm{h}
Rychlost, dráha, čas: vzájemný pohyb těles
Pokud se pohybuje více těles, můžeme zkoumat jejich vzájemný pohyb.
Vzájemná rychlost dvou těles (těleso 1 a těleso 2) je rozdílem jejich rychlostí. Pokud budeme jednotlivé rychlosti značit indexy, můžeme pro vzájemnou rychlost použít v.
v=v_1-v_2
(pokud je důležitý směr a pokud rozlišujeme, zda jde o rychlost 1. tělesa vůči 2. nebo naopak, používá se také v_{12} resp v_{21})
Pokud se k sobě tělesa přibližují, určuje vzorec t=\frac{s}{v} čas setkání – dosazujeme do něj právě vzájemnou rychlost a počáteční vzdálenost těles (i pro tu používáme přímo písmeno s protože pro dráhy jednotlivých těles pravděpodobně použijeme s_1 a s_2).
Dráhy jednotlivých těles a místo setkání je možné poté dopočítat, když dosadíme do vzorce pohybu jednotlivých těles vypočtený čas setkání t (např. s_1=v_1\cdot t, nebo s_2=v_2\cdot t).
NahoruRovnoměrný a nerovnoměrný pohyb
Pohyb dělíme na rovnoměrný a nerovnoměrný podle toho, jestli se mění velikost rychlosti. U tohoto dělení naopak nezáleží na tom, jestli se mění směr pohybu (směr rychlosti).
rovnoměrný pohyb = velikost rychlosti je stále stejná, zrychlení je nulové, nebo kolmé na směr pohybu (pohyb po kružnici)
nerovnoměrný pohyb = velikost rychlosti se mění, zrychlení není nulové
Zrychlení
Pokud se rychlost pohybu mění, charakterizuje tyto změny veličina jménem zrychlení. Značíme jej a a je to změna rychlosti za změnu času.
a=\frac{\Delta v}{ \Delta t }
- Rychlost lodi vzrostla o 6 m/s během 3 s. Zrychlení bylo 2 m/s².
Jednotkou zrychlení je \mathrm{m/s^2}.
Zejména v kinematice můžeme zrychlení brát jako změnu velikosti rychlosti. Pokud je stále stejné, jde o pohyb rovnoměrně zrychlený nebo pohyb rovnoměrně zpomalený.
Pro rychlost rovnoměrně zrychleného pohybu platí:
v=v_0+a\cdot t nebo jednodušeji v=a\cdot t (pokud je počáteční rychlost v_0 nulová)
Vztah pro dráhu je pak:
s=v_0t+\frac{1}{2}a t^2 nebo jednodušeji s=\frac{1}{2}a t^2 (pokud je počáteční rychlost v_0 nulová)
V případě rovnoměrně zpomaleného pohybu (rychlost se rovnoměrně snižuje), používáme obvykle vztahy v=v_0-a\cdot t pro rychlost a s=v_0t-\frac{1}{2}a t^2 pro dráhu.
Zjednodušené vztahy (v_0=0) v tomto případě nemají smysl, protože musíme mít z čeho zpomalovat.
Zpomalení a záporné zrychlení
Je i alternativa používat pro zpomalený pohyb stejné vztahy jako pro pohyb zrychlený a dosazovat záporné hodnoty zrychlení a. V následujících cvičeních ale není použita.
Přesnější definice zrychlení je změna vektoru rychlosti za změnu času.
\vec a=\frac{\Delta \vec v}{ \Delta \vec t }
Zrychlení je podle této definice nenulové i u rovnoměrného pohybu po kružnici a každého křivočarého pohybu (mění se směr vektoru rychlosti).
NahoruDráha zrychleného pohybu
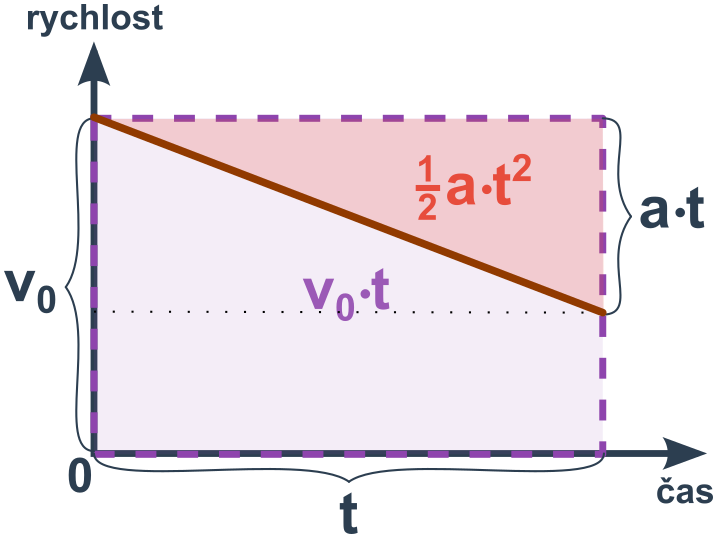
Graf závislosti rychlosti na čase u rovnoměrného pohybu vypadá takto:
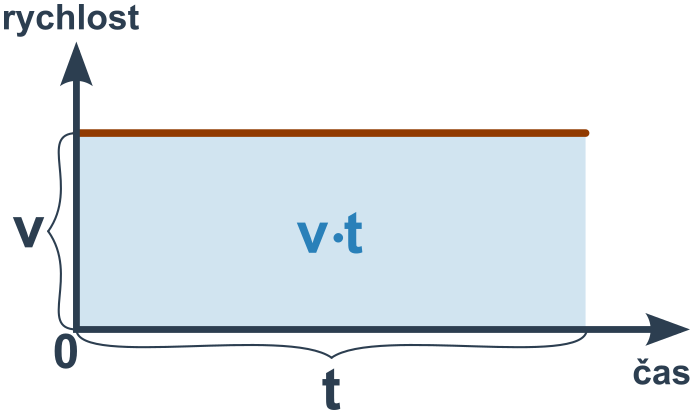
Plocha pod křivkou rychlosti má obsah v\cdot t (obsah obdélníka) což je přesně rovno dráze rovnoměrného pohybu. To platí obecně – obsah plochy pod křivkou rychlosti v grafu v/t je roven dráze.
U rovnoměrně zrychleného pohybu (konstantní a) nejde o obdélník, plocha je ale stejná jako plocha obdélníka o výšce průměrné rychlosti \bar v (plocha △ a △ je totiž stejná).
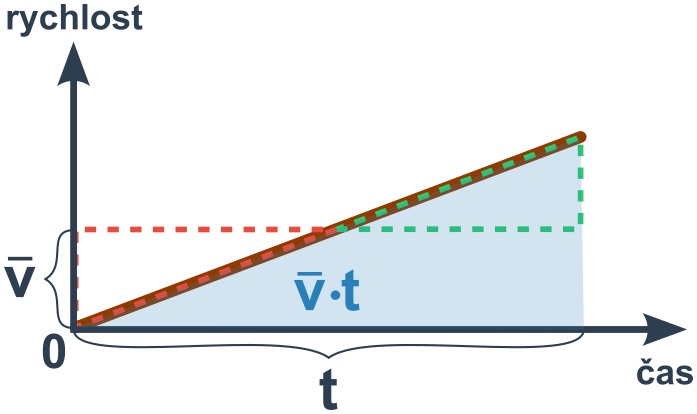
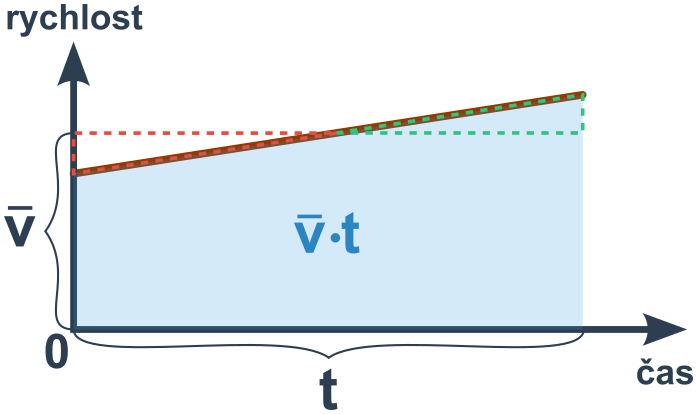
Dráhu rovnoměrně zrychleného pohybu počítáme v různých situacích:
Pohyb začíná z klidu
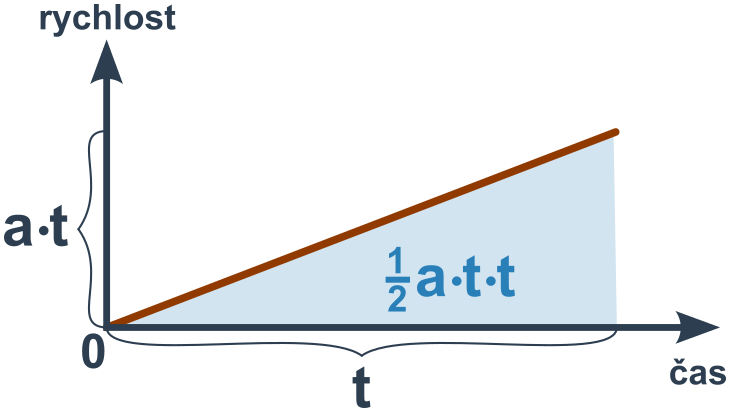
Pro rychlost platí v=a\cdot t (přímá úměra). Dráha (obsah pod křivkou) je rovna:
s=\frac{1}{2}at^2
Příklad: Dráha rozjíždějícího se auta
Auto se z klidu rozjíždí se zrychlením 2 m/s². Jakou dráhu ujede za 3 s?
- Zrychlení a je 2 m/s² a čas t je 3 s.
- Můžeme je přímo dosadit do s=\frac{1}{2}at^2.
- s=\frac{1}{2}at^2=\frac{1}{2}2\cdot 3^2\,\mathrm m=9\,\mathrm m
- Auto urazilo 9 m.
Příklad: Dráha valícího se kamene (grafická úvaha)
Na svahu se uvolnil kámen a začal se kutálet dolů se zrychlením 0,5 m/s². Jakou dráhu urazí za 10 s?
- Zrychlení a je 0,5 m/s² a čas t je 10 s.
- V grafu v-t je první odvěsna △ (vodorovná) rovna t, tedy 10 s.

- Druhá odvěsna je rovna a\cdot t, tedy 5 m/s– to je vlastně konečná rychlost v čase 10 s.
- Obsah △ je polovina součinu odvěsen. Tedy s=\frac{1}{2}\cdot 10\cdot 5\,\mathrm m=25\,\mathrm m
- Kámen tedy urazil 25 m.
Těleso se už pohybuje rychlostí v_0 a zrychluje
S nenulovou v_0 máme rychlost v=v_0+a\cdot t. Pak je dráha rovna součtu:
s=v_0\cdot t + \frac{1}{2}at^2
I to můžeme vyčíst z grafu (celková plocha = součet ▯ v_0\cdot t a △ \frac{1}{2}at^2):
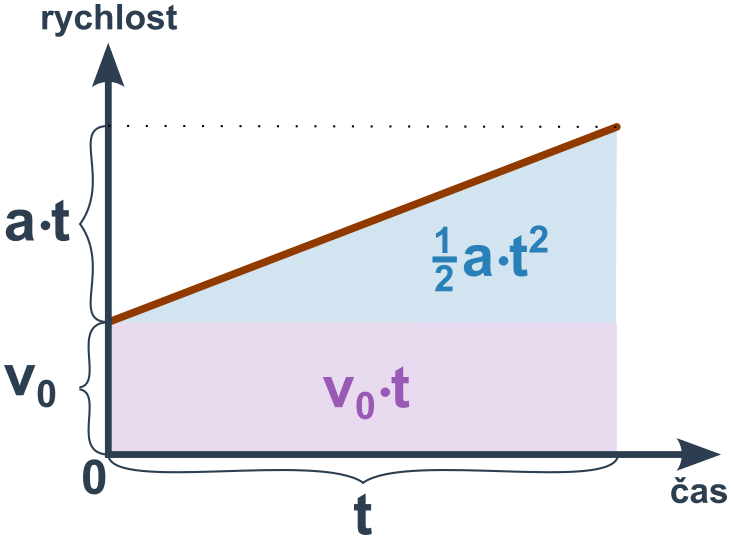
Příklad: Nástup závodníka do finiše
Závodník v cílové rovince z původní rychlosti 5 m/s rovnoměrně zrychloval (o 1 m/s²). Jak daleko byl cíl, pokud doběhl za 4 s?
- Zrychlení a je 1 m/s², čas t je 4 s a rychlost v_0 je 5 m/s.
- Můžeme je přímo dosadit do s=v_0\cdot t+\frac{1}{2}a t^2.
- s=v_0\cdot t+\frac{1}{2}at^2=5\cdot 4 + \frac{1}{2}1\cdot 4^2\,\mathrm m=20+8\,\mathrm m=28\,\mathrm m
- Když začal zrychlovat, byl závodník 28 m od cíle.
Těleso se už pohybuje rychlostí v_0 a zpomaluje
Platí totéž co v předchozím bodě, jen obsah △ odečítáme.
s=v_0\cdot t -\frac{1}{2}at^2
Příklad: Brzdění auta
Řidič plynule zpomaloval z 30 m/s po dobu 2 se zrychlením 5 m/s². Jakou dráhu urazil?
- Čas t je 2 s, rychlost v_0 je 30 m/s a zrychlení a je 5 m/s².
- Můžeme tedy přímo dosadit do s=v_0\cdot t-\frac{1}{2}a t^2.
- s=v_0\cdot t-\frac{1}{2}at^2=30\cdot 2 - \frac{1}{2}5\cdot 2^2\,\mathrm m=60-10\,\mathrm m=50\,\mathrm m
- Řidič během těch dvou sekund zpomalování urazil 50 m.
Grafy pohybu
Grafy pohybu jsou nejčastěji 2-D grafy, jak je známe z matematiky, které zobrazují vývoj nějaké veličiny popisující pohyb (y-ová, svislá osa) v závislosti na čase (x-ová, vodorovná osa).
Zobrazované veličiny jsou typicky poloha (na trati nebo dráze, obvykle nejde o skutečnou 3-D polohu), uražená dráha, nebo rychlost. Ale mohli bychom zobrazovat i např. zrychlení nebo jiné, obskurnější veličiny. Jde vlastně o záznam „měření“ dané veličiny v čase.
Z grafu pohybu můžeme:
- Zjistit typ grafu, o který se jedná (zaznamenaná veličina, počet těles, …).
- Získat základní informace o pohybu podle tvaru křivky v grafech. Jak v grafech polohy/dráhy, tak rychlosti.
- Odečítat hodnoty v grafech polohy i rychlosti v konkrétních bodech pohybu (např. v jakém čase byla rychlost nejvyšší).
- Vypočítat další veličiny (například rychlost z grafu dráhy nebo dráhu z grafu rychlosti).
Typy grafů pohybu
Rozlišujeme dva nejčastější typy grafů. Ty které zobrazují prostorovou veličinu (poloha, dráha) a ty které zobrazují rychlost. Poznáme to podle toho jak je označena svislá osa grafu. Kromě toho mohou existovat graf i jiných veličin (např. zrychlení), ale většinou je nepoužíváme.
Přitom jeden graf může zachycovat pohyb jednoho, ale i více těles (pak se v něm nachází více křivek, nebo sad bodů).
NahoruGrafy polohy/dráhy: základy
Grafy polohy (zde značíme x) a uražené dráhy (zde značíme s) jsou často vzájemně zaměnitelné, někdy ale ne. Dráha totiž narůstá i když se otočíme a začneme se po trase vracet. Poloha ne. Dráha navíc obvykle začíná na nule, což poloha nemusí. Ilustrují to následující grafy stejného pohybu dvou těles – jednou pro polohu, podruhé pro dráhu.
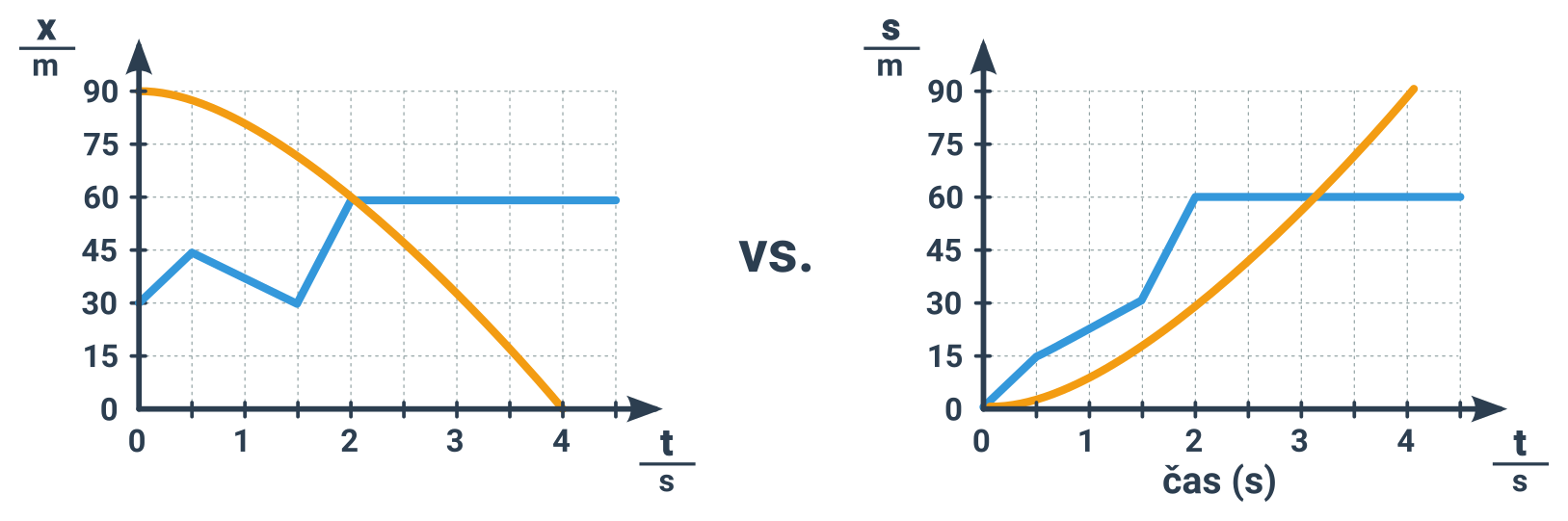
Platí, že čím strmější je křivka, tím rychlejší je pohyb. To znamená několik základních pouček pro kvalitativní pochopení zobrazeného pohybu:
- zlom křivky = náhlá změna rychlosti
- ohýbání křivky = plynulá změna rychlosti
- přímé úseky = rovnoměrný pohyb
- vodorovná část křivky = těleso stojí na místě
Příklad: Dráha auta a cyklisty
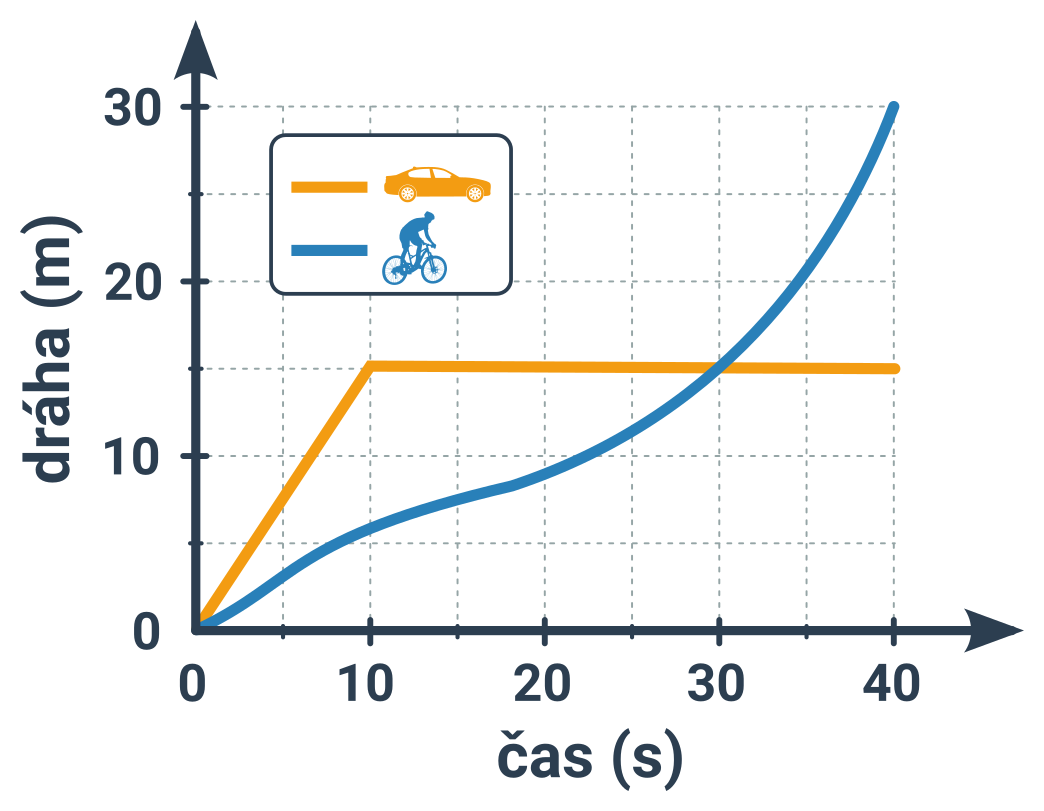
- Podle legendy je auto znázorněno oranžovou křivkou.
- Ta zpočátku (pravý kraj grafu) stoupá, auto se tedy pohybuje (dráha roste). A protože je tento úsek úsečka (nezakřivená), pohyb auta je tu rovnoměrný.
- Poté se křivka náhle zlomí do vodorovna. Auto tedy v mžiku změnilo rychlost na nulovou a stojí na místě. Až do konce (křivka je vodorovná až do konce grafu).
- Modrá křivka cyklisty je stále skloněná. Cyklista se tedy celou dobu pohybuje. Sklon se ale mění (nejde o úsečku). Jeho pohyb je tedy nerovnoměrný.
- Nejstrmější je křivka na konci, tehdy má tedy cyklista nejvyšší rychlost.
Grafy polohy/dráhy: odečítání údajů
Pro odečítání nějaké hodnoty z grafu existuje několik základních úkolů:
1. Máme daný bod na křivce a máme zjistit jeho souřadnici (časovou nebo polohovou/dráhovou).
Jednoduše z tohoto bodu vedeme kolmici na osu žádané veličiny. Poloha průsečíku pak odpovídá hledané hodnotě.
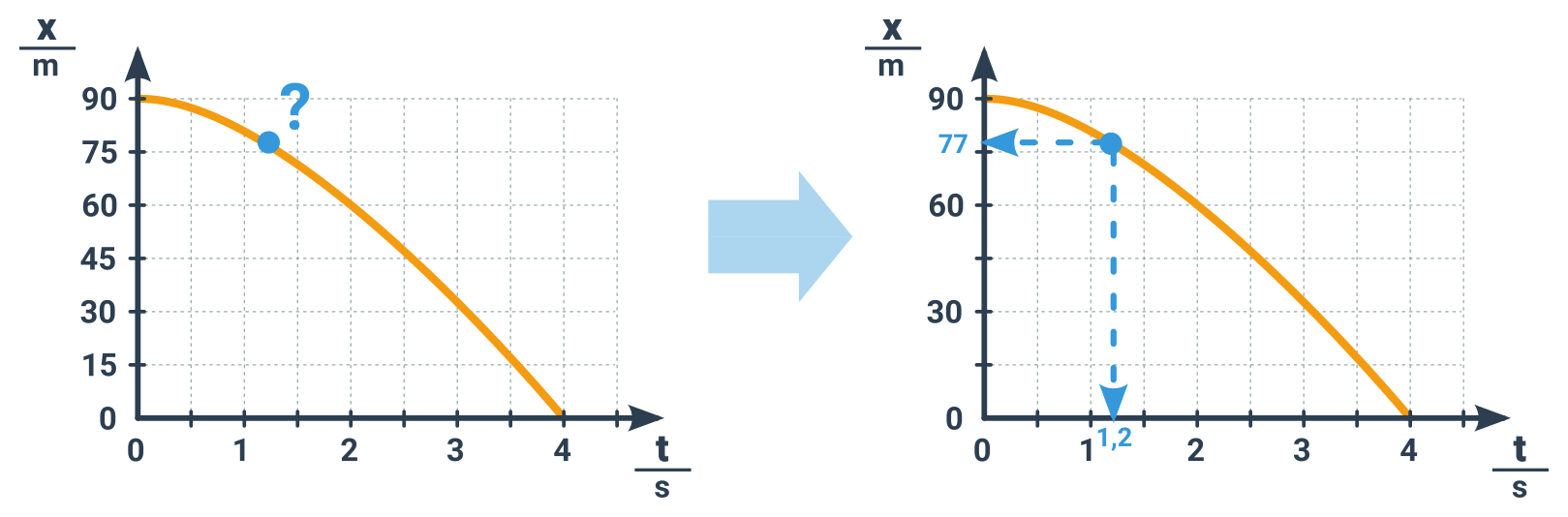
Nejčastěji když má samotný bod křivky nějaký význam, například zastavení tělesa (křivka se tam láme do vodorovna). Často jej tedy musíme nejprve identifikovat (můžete procvičit i zde)
Příklad: Poloha na konci
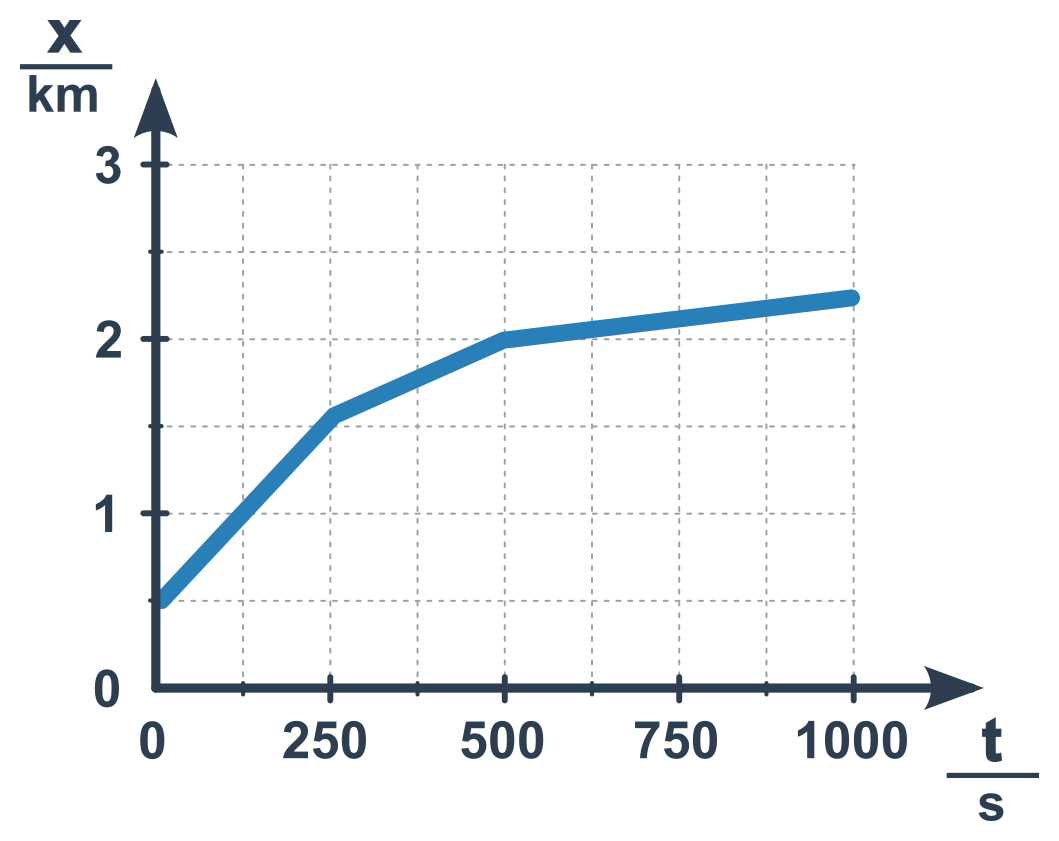
- Jakou polohu má těleso na konci sledování pohybu.
- Zjevně jde o bod na pravém konci křivky.
- Z tohoto bodu jedeme vodorovně doleva ke svislé ose.
- Protneme ji asi půl dílku nad 2. Velikost dílku je 0,5 km.
- Proto je poloha tělesa na konci 2 plus polovina z 0,5. Tedy 2,25 km.
2. Pro daný čas hledáme polohu/dráhu tělesa.
Vedeme z tohoto časového bodu kolmici. Hledáme průsečík s křivkou pohybu. Z něj vedeme kolmici na osu polohy podobně jako v bodu 1.
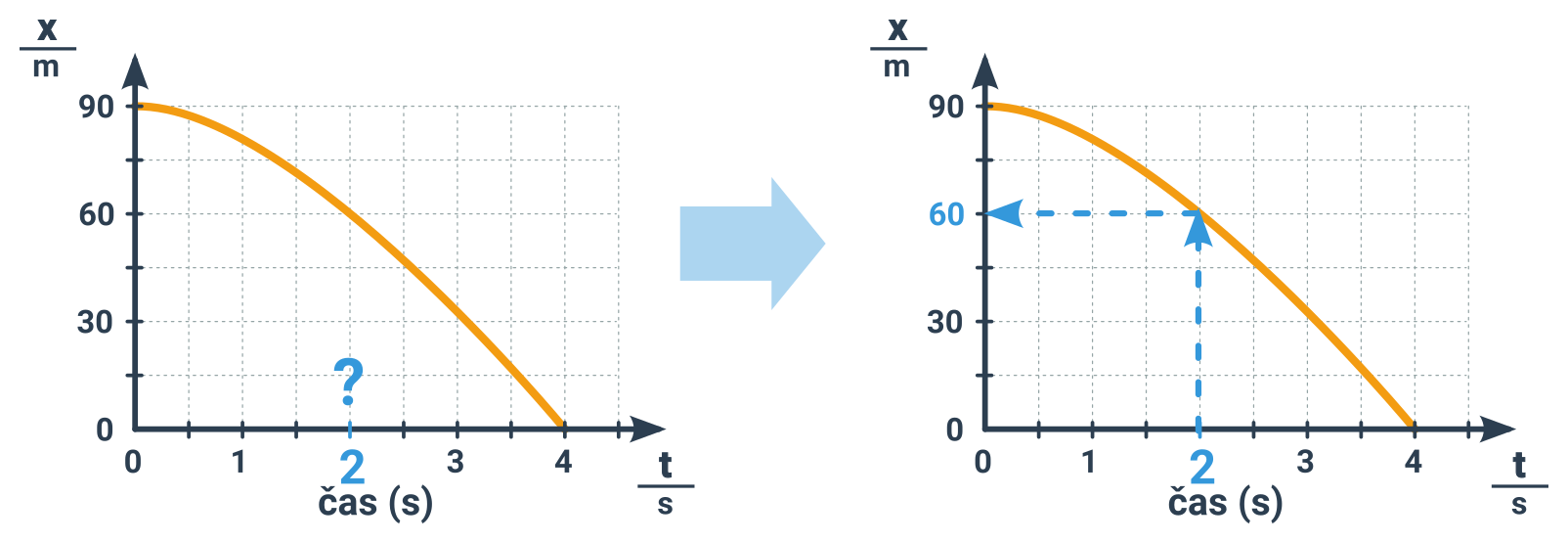
3. Pro určitou polohu/dráhu hledáme čas, kdy se na ni těleso nachází.
Postup je obdobný jako v bodě 2, jen začínáme ze svislé osy.
Ne vždy ale existuje řešení (průsečík s křivkou). Pak můžeme říct, že taková situace nenastane nikdy.
Příklad: Určení času při dosažení polohy 2 km

- Chceme znát čas, kdy je těleso na poloze 2 km.
- Najdeme na svislé ose 2 km a vedeme z ní vodorovnou čáru (zde už je naznačena mřížkou).
- Tam, kde se protne s křivkou pohybu, je náš bod. Je to přesně ve druhém zlomu křivky.
- Kolmo dolů pod tímto bodem dojdeme na časovou osu, na hodnotu 500 s.
Grafy rychlosti: základy
Grafy rychlosti zobrazují velikost rychlosti v čase. Nenesou informaci o poloze, byť uraženou dráhu z nich zjistit můžeme (čím větší plocha pod křivkou, tím větší uražená dráha). Z tvaru a polohy křivky můžeme určit některé kvalitativní vlastnosti pohybu:
- vodorovná část křivky na nule = těleso stojí na místě
- vodorovná část křivky = rovnoměrný pohyb
- přímé úseky (šikmo) = rovnoměrně zrychlený/zpomalený pohyb
- zakřivené úseky = nerovnoměrně zrychlený/zpomalený pohyb
Grafy rychlosti: odečítání údajů
Pro odečítání z grafů rychlosti platí to stejné jako pro odečítání údajů z grafů polohy a dráhy. Jen na svislé ose odečítáme rychlosti.
Řešíme tedy stejné tři úlohy – hledáme buď souřadnice bodu (který často musíme identifikovat), hodnotu rychlosti v daném čase, nebo čas, kdy má rychlost určitou hodnotu.
NahoruVýpočty rychlosti a dráhy z grafů
I z grafů dráhy/polohy můžeme určit rychlost a z grafů rychlosti dráhu. Ne vždy je to jednoduché udělat přesně, ale alespoň odhadnout je můžeme vždy.
Výpočet rychlosti z grafu polohy/dráhy
Můžeme určovat průměrnou rychlost celého pohybu (v=s/t) nebo nějakého jeho úseku (v=\Delta s/ \Delta t). Symbol \Delta značí rozdíl hodnot, např. \Delta t = t_\mathrm{konec}-t_\mathrm{zacatek}.
Odečteme údaje na osách pro oba krajní body úseku a dosadíme do výpočtu:
v=\frac{s_\mathrm{konec}-s_\mathrm{zacatek}}{t_\mathrm{konec}-t_\mathrm{zacatek}}
Příklad: Celková průměrná rychlost pohybu se změnou rychlosti
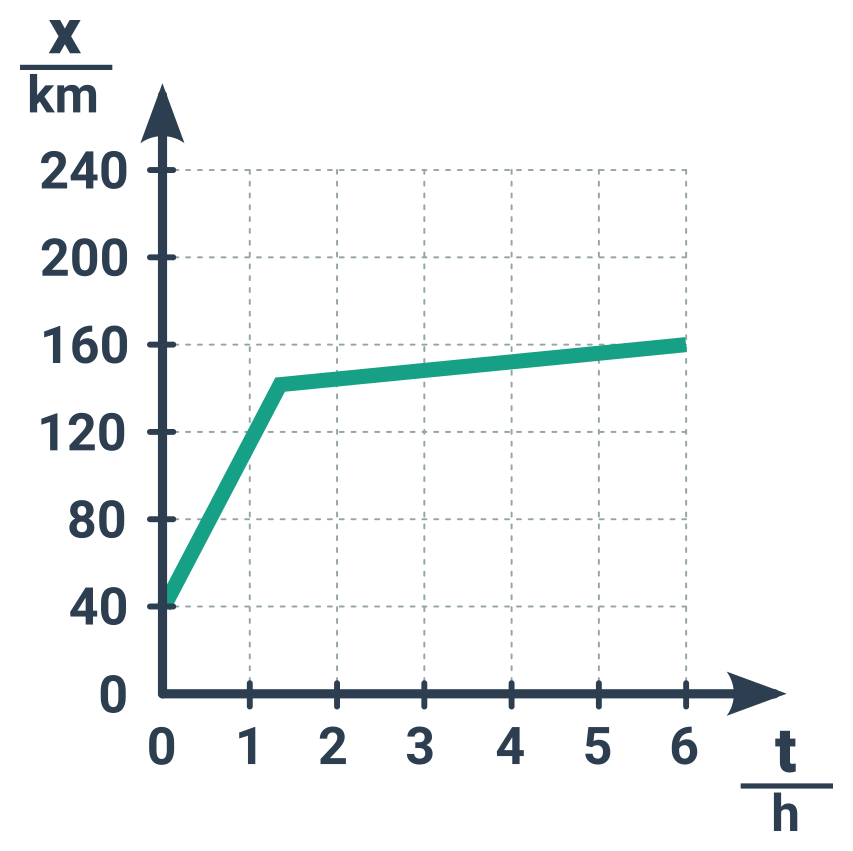
Dosadíme krajní hodnoty do vzorce (160 km a 40 km do čitatele, 6 h a 0 h do jmenovatele) a dostaneme průměrnou rychlost

Výpočet dráhy z grafu rychlosti
V grafu rychlosti tělesa je dráha vlastně obsahem plochy pod křivkou rychlosti. Obecně je to těžké. Někdy jsou ale pod křivkou jednoduché tvary, jejichž obsah známe. Jindy obsah můžeme alespoň přibližně odhadnout.
Obdélníky:
Obsah obdélníka je strana krát strana, zde tedy vlastně s=v\cdot t.
Příklad: Dráha cyklisty
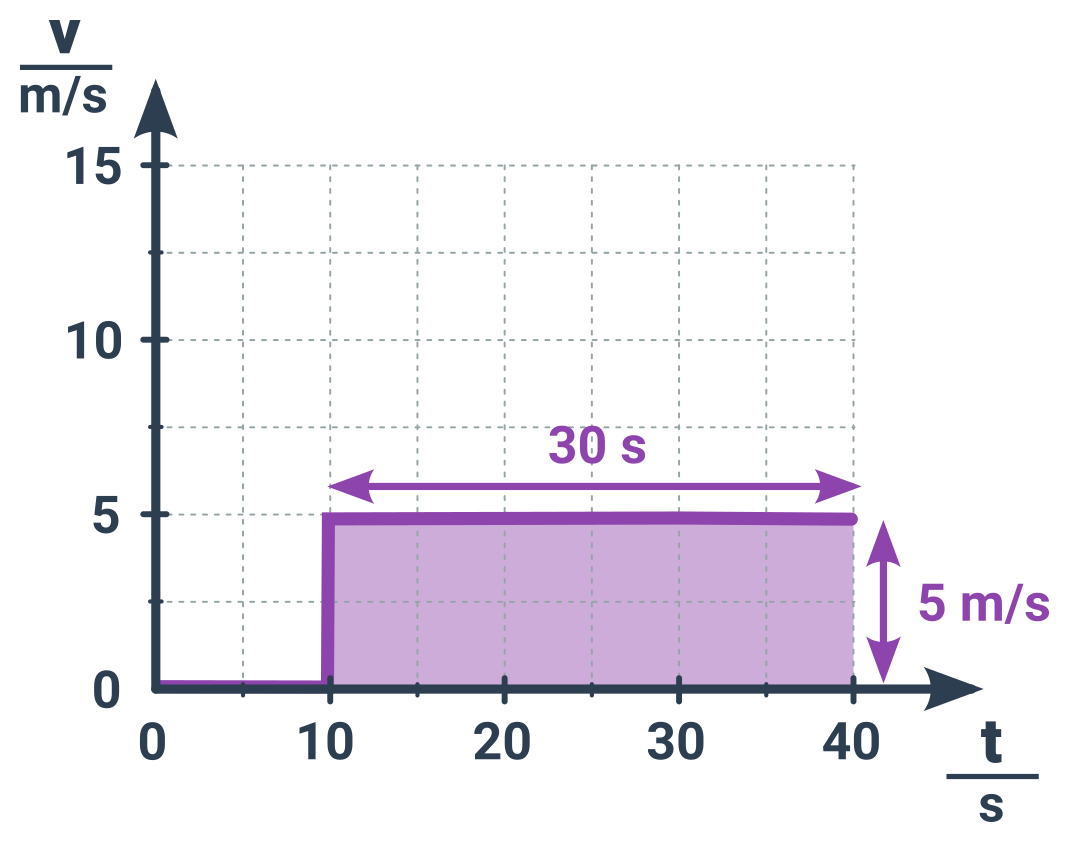
Oblast pod křivkou je obdélník, když jeho rozměry vynásobíme dostaneme ihned výslednou dráhu.

Pozn.: Pravoúhlý trojúhelník má obsah jako polovina obdélníka.
Postup použitelný i pro složitější tvary (minimálně odhad) využívá mřížky grafu. Spočítáme obsah jednoho čtverce mřížky a pak vynásobíme počtem čtverců pod křivkou (nemusí být celé číslo).
Příklad: Dráha cyklisty pomocí mřížky
Z grafu
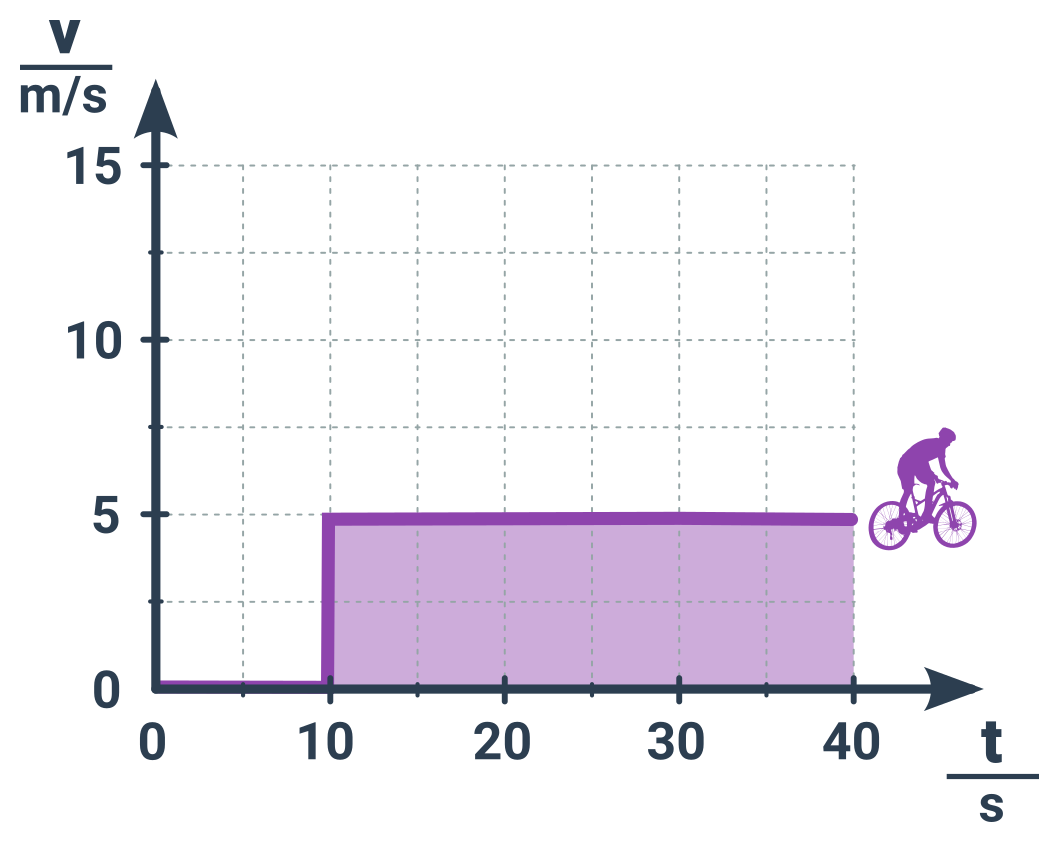
určíme obsah jednoho čtverce mřížky

Pod křivkou je 12 takových čtverců, takže

Vrhy a pády
Vrhy a pády jsou speciálním případem pohybu rovnoměrně zrychleného. Popisují pohyb těles, kterými házíme kolem sebe nebo které padají.
Platí jen tam kde můžeme zanedbat odpor vzduchu (pád hopskulky z okna je ok, ale pád kroupy z mraku nebo listu papíru ze stolu ne) a v omezeném prostoru (ve kterém se téměř nemění zemská přitažlivost, ne pro hod ze země do stratosféry).
- Základem je umět určit o jaký typ vrhu se jedná (volný pád, vrh svislý, vrh vodorovný, vrh šikmý)
- Poté můžeme určit některé vlastnosti takového vrhu.
- Jednotlivým typům se pak můžeme věnovat detailněji, s výpočty a vzorci – aktuálně zde najdeme procvičování volného pádu
Poznávání vrhů
Klasická mechanika popisuje 4 vrhy/pády. Volný pád, vrh svislý, vrh vodorovný a vrh šikmý.
Rozpoznáme je podle trajektorie a rychlosti v:
Trajektorie
- vrh svislý a volný pád → rovná (část přímky)
- vrh vodorovný a vrh šikmý → zakřivená (část paraboly)
U vodorovného vrhu a volného pádu navíc trajektorie začíná nejvyšším bodem.
Rychlost
- volný pád → počáteční úplně nulová, pak svisle směrem dolů
- vrh svislý → počáteční svislý směr, v průběhu svislý směr nebo nulová
- vrh vodorovný → počáteční vodorovný směr, pak vždy šikmo dolů
- vrh šikmý → počáteční šikmý směr, v průběhu i vodorovný (na vrcholu)
V průběhu všech vrhů se vodorovná složka rychlosti (obvykle značená v_\mathrm x) nemění, svislá (v_\mathrm y) ale ano.
Matematicky: vodorovný směr rychlosti znamená v_\mathrm y = 0, svislý směr rychlosti znamená v_\mathrm x=0.
NahoruVlastnosti vrhů
Několik veličin a vlastností, které se pojí s vrhy:
Obecné vlastnosti
- zanedbáváme odpor vzduchu (jinak by byly výpočty mnohem komplikovanější)
- trajektorií je část paraboly nebo úsečka (u vrhu svislého a volného pádu)
- pro popis volíme obvykle dvě souřadnice x (vodorovná) a y (svislá), vrh totiž probíhá v rovině
Veličiny
Rychlost na počátku značíme v_0, v průběhu vrhu pak v. Rychlost dopadu pak v_\mathrm d.
- můžeme je rozložit na vodorovnou a svislou složku (v_\mathrm{0x}, v_\mathrm{0y}, v_\mathrm{x}, v_\mathrm{y}, v_\mathrm{dx} nebo v_\mathrm{dy})
- vodorovná složka se nemění (v_\mathrm{x}=v_\mathrm{0x})
- u vrhu šikmého jsou rychlosti ve stejných výškách stejně velké a svírají stejný úhel s vodorovným směrem (jen v_y se otočí směrem dolů)
Polohu tělesa popisují právě souřadnice x a y
- protože je v_\mathrm{x}=v_\mathrm{0x}, probíhá v souřadnici x rovnoměrný pohyb
- souřadnice y se mění nerovnoměrně – jde vlastně o rovnoměrně zrychlený pohyb se zrychlením g
Čas dopadu se značí obvykle t_\mathrm d a jde o dobu od začátku vrhu do dopadu. Závisí vždy na v_\mathrm{0y} a často na počáteční svislé poloze y_0 (respektive výšce nad zemí h).
NahoruVolný pád
Volný pád znamená, že těleso padá z klidu z počáteční nenulové výšky. Protože je v_0 nula a protože v_\mathrm x se u vrhů nemění, bude v_\mathrm x vždy nulová. Pak není rozdíl mezi svislou rychlostí v_\mathrm y a celkovou rychlostí v, dále tedy mluvíme jen o v.
Pohyb tedy probíhá pouze ve svislém směru a popisuje jej jen souřadnice y. Počáteční svislou polohu y_0 většinou značíme také jako výšku pádu h.
Jde o rovnoměrně zrychlený pohyb se zrychlením g a počáteční rychlostí v_\mathrm {0}=0 (viz výše). V čase t je tedy rychlost rovna g\cdot t a dráha rovna \frac{1}{2}gt^2.
Většinou nás zajímá čas dopadu t_\mathrm d. Můžeme jej vyjádřit z výšky h, protože čase t_\mathrm d musí být dráha rovna právě celé této výšce. Platí tedy rovnice h=\frac{1}{2}gt_\mathrm{d}^2 a úpravou platí i:
t_\mathrm{d}=\sqrt{\frac{2h}{g}}
Nyní můžeme z výšky h vyjádřit i rychlost dopadu v_\mathrm {d}=g\cdot t_\mathrm d. Pokud totiž za t_\mathrm d dosadíme \sqrt{\frac{2h}{g}}, dostaneme v_\mathrm {d}=g\cdot \sqrt{\frac{2h}{g}}, po úpravě:
v_\mathrm {d}=\sqrt{2hg}
NahoruPohyb po kružnici
Z nepřímočarých pohybů je nejdůležitější rovnoměrný pohyb po kružnici. Popisuje situace jako točení na kolotoči, prádlo v bubnu ždímačky nebo otáčení planety Země. Přibližně odpovídá i řadě složitějších situací (např. pohyb v trolejbusu v zatáčce).
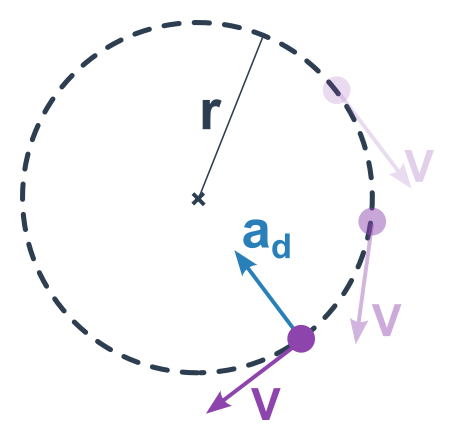
Tedy trajektorií je kružnice. Rychlost v je tečnou k trajektorii (i proto se nazývá obvodová) a má konstantní velikost, mění se ale směr. Zrychlení (které právě popisuje změny směru rychlosti) směřuje do středu kružnice. Říká se mu proto dostředivé a značíme jej a_\mathrm d. Má velikost:
a_\mathrm d=\frac{v^2}{r}
Často nás nezajímá, jak rychle se pohybujeme, ale jak rychle se otáčíme dokola (úhel za jednotku času). Proto definujeme úhlovou rychlost \omega. Pro rovnoměrný pohyb po kružnici je \omega konstantní a úhel otočení \varphi je přímo úměrný času.
Platí vztahy jako \omega=\frac{v}{r} resp. v=\omega\cdot r. Po dosazení za v tak můžeme dostat alternativní vztah pro a_\mathrm d:
a_\mathrm d=\omega^2\cdot r
Nahoru
