Výpis souhrnů
Elektrické obvody
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Spojování rezistorů
Rezistory jsou součástky, jejichž úkolem je klást elektřině odpor. Samy jsou někdy nepřesně označované jako „odpory“. Odbor je hlavní vlastnost rezistorů, ale mají ji i jiné součástky. Elektrická energie se v nich přeměňuje na teplo.
Hodnota el. odporu je na nich nejčastěji znázorněna textově (např. 1k2 znamená „jedno-kilo-dvě“ tedy 1200 ohmů) nebo graficky pomocí různobarevných proužků.
Často nás zajímá, jaký celkový odpor má více rezistorů v obvodu dohromady (např. pro výpočet celkového proudu obvodem). Záleží na tom, jestli jsou v obvodu spojeny sériově nebo paralelně.
Sériově zapojené rezistory
To znamená jeden za druhým (viz obrázek). Oběma mj. teče stejný proud I.
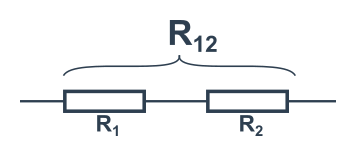
Z toho (a Ohmova zákona) se dá odvodit, že jejich celkový odpor je normálním součtem jednotlivých odporů. Tedy:
R_{12}=R_1+R_2
Paralelně zapojené rezistory
To znamená každý na jiné větvi proudu (tzv. vedle sebe, viz obrázek). Na obou musí být stejné napětí U.
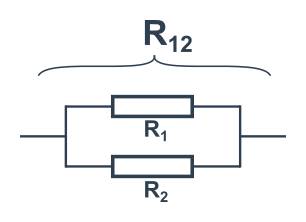
Z toho (a Ohmova zákona) se dá odvodit, že jejich celkový odpor splňuje rovnici:
\frac{1}{R_{12}}=\frac{1}{R_1}+\frac{1}{R_2}
Jde tedy o podobnou rovnici, ale s převrácenými hodnotami. Matematickými úpravami můžeme dojít k vyjádření R_{12} jako:
R_{12}=\frac{R_1R_2}{R_1+R_2}
Více rezistorů
Pro více rezistorů (a obecně více odporů) platí podobné vztahy.
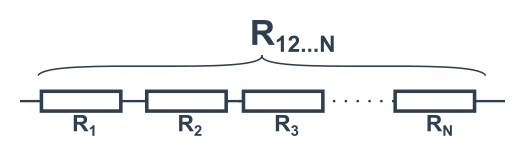
Sériové zapojení N členů: R_{12..N}=R_1+R_2+R_3+\cdots+R_N
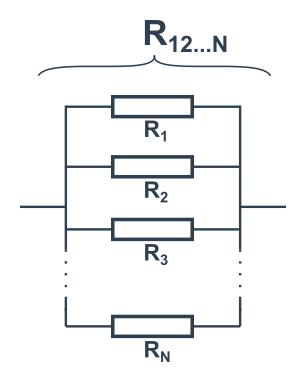
Paralelní zapojení N členů: \frac{1}{R_{12..N}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\cdots+\frac{1}{R_N}
(úprava do tvaru R_{12..N}= je samozřejmě možná, výsledné vzorce ale vypadají podle počtu rezistorů různě)
Složitější zapojení
Zjednodušujeme podle pravidel výše postupně od nejmenších vnitřních celků (dvojic).
Takto ano: 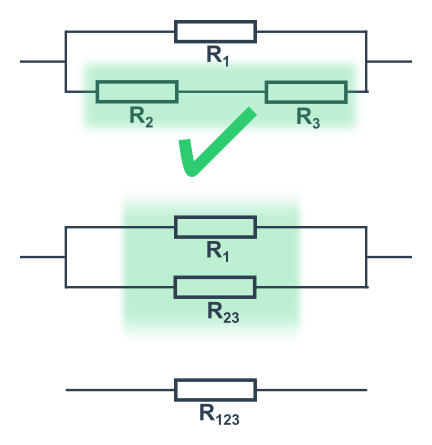
Takto ne (vybraná dvojice netvoří samostatné paralelní zapojení, k pravému uzlu se musí jít přes R_3):
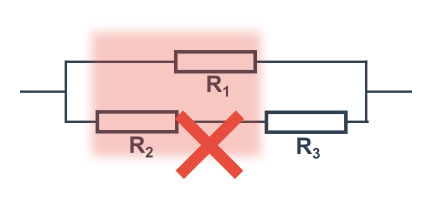
Spojování kondenzátorů
Pravidla pro počítání celkové kapacity více kondenzátorů (respektive kapacit obecně) jsou velmi podobná jako ta pro rezistory. Akorát přesně naopak.
Paralelní zapojení
Pro paralelní kondenzátory platí podobný vzorec jako pro sérii rezistorů (tedy prostý součet):
C_{12}=C_1+C_2
Případně pro více paralelně zapojených kondenzátorů je celková C rovna C=C_1+C_2+C_3+\cdots
Sériové zapojení
Pro sériové zapojení kondenzátorů platí podobný vzorec jako pro paralelní rezistory. tedy \frac{1}{C_{12}}=\frac{1}{C_{1}}+\frac{1}{C_{2}} což můžeme upravit na
C_{12}=\frac{C_{1}+C_{2}}{C_{1} C_{2}}
Pro více sériově zapojených kondenzátorů splňuje celková C rovnici \frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}+\cdots (ze které si musíme C vyjádřit).
Složitější zapojení
Zjednodušujeme opět od nejmenších celků, stejně jako rezistory.
Nahoru

 Čeština
Čeština Matematika
Matematika Angličtina
Angličtina Informatika
Informatika Biologie
Biologie Němčina
Němčina Umíme to
Umíme to Zeměpis
Zeměpis Chemie
Chemie Dějepis
Dějepis Fyzika
Fyzika ZSV
ZSV
