Výpis souhrnů
Jednoduché stroje
Prohlížíte si souhrny informací k určitým tématům. Systémy Umíme se zaměřují hlavně na jejich procvičování. Ke cvičením k jednotlivým podtématům se dostanete pomocí odkazů níže.
Podtémata
Princip páky je jedním z nejpraktičtějších využití momentu síly. Páka nám usnadňuje některé věci, na které bychom normálně neměli dostatečnou sílu, například rozlousknout ořech.
Páka a síly
Mějme těleso, které se může otáčet kolem nějaké osy nebo opěrného bodu (kleště, houpačka, zahradní kolečka). Sílu působící na jednom místě F_1 (např. tíhu nákladu) můžeme vyrovnávat druhou silou F_2 a držet páku v rovnováze. Síly působí ve vzdálenostech od osy r_1 a r_2 a nemusí být stejně velké.
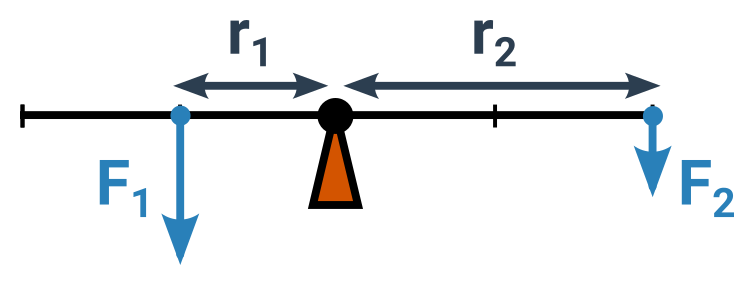
V rovnováze je poměr velikostí sil opačný než poměr jejich ramen. Zde procvičíme jednodušší případ, kdy jsou síly kolmé na úsečky r_1 a r_2. Pak je ramenem síly přímo vzdálenost od osy. Pak platí, že v rovnováze je poměr velikostí sil opačný než poměr jejich vzdáleností od osy.
F_1:F_2=r_2:r_1
Pozn.: Ve cvičeních je grafika sil pouze ilustrační – délka šipek neodpovídá velikosti sil.
Příklad: Kdy budou síly v rovnováze stejně velké?
Síly v rovnováze nemusí být stejně velké. Ale kdy stejně velké budou?
- Platí F_1:F_2=r_2:r_1.
- Pokud jsou obě síly stejně velké, je F_1:F_2 rovno jedné.
- Jednička tedy musí být i poměr r_2:r_1.
- To znamená, že obě vzdálenosti musí být stejné.
Páka a hmotnosti
Když nepočítáme se silami, ale s hmotnostmi, platí pro rovnováhu obdobný vztah.
m_1:m_2=r_2:r_1
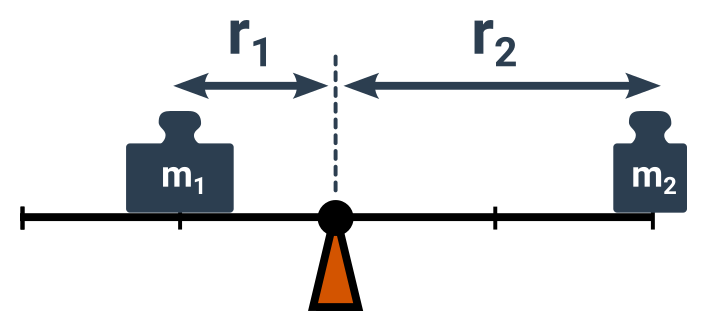
Příklad: Na houpačce
Kdo musí na houpačce sedět víc u středu, aby se mohli pohodlně houpat? Maminka nebo holčička? 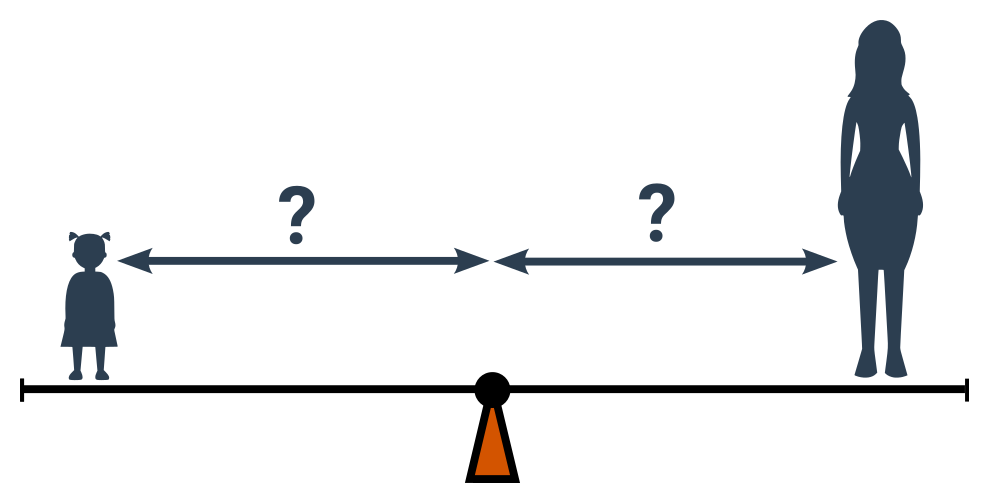
- Rovnováha (a snadné houpání) nastane, když jsou vzdálenosti v opačném poměru než hmotnosti (m_1:m_2=r_2:r_1).
- Holčička má menší hmotnost.
- Holčička tedy musí mít větší vzdálenost od středu.
- Blíže ke středu si tedy bude muset sednou maminka.
Síly a hmotnosti dohromady
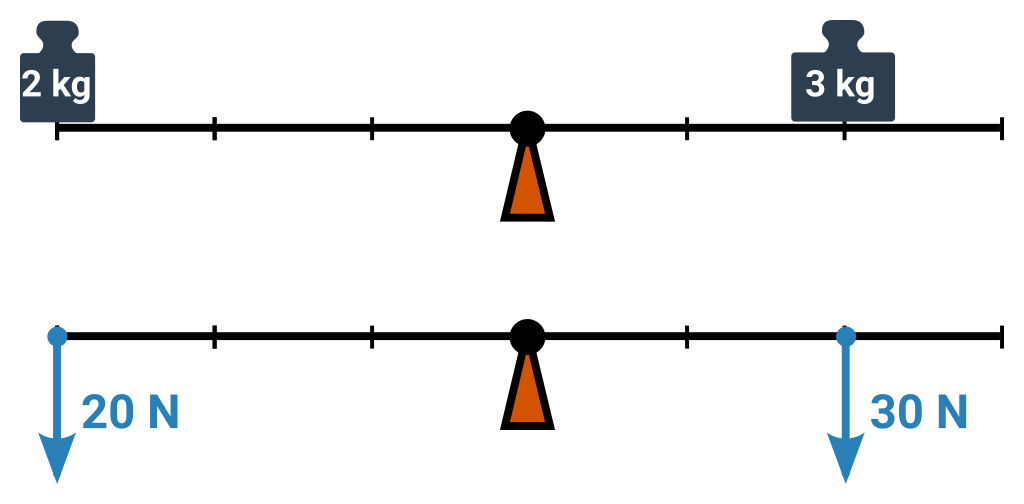
Pokud kombinujeme hmotnost a síly, musíme hmotnosti převést na tíhové síly. Každý kg odpovídá síle asi 10 N. Bedna o 3 kg, tedy bude působit silou 30 N. Člověk s 85 kg pak silou 850 N.
Příklad: Naložený trakař
Jakou silou musíme zvedat řídítka trakaře? 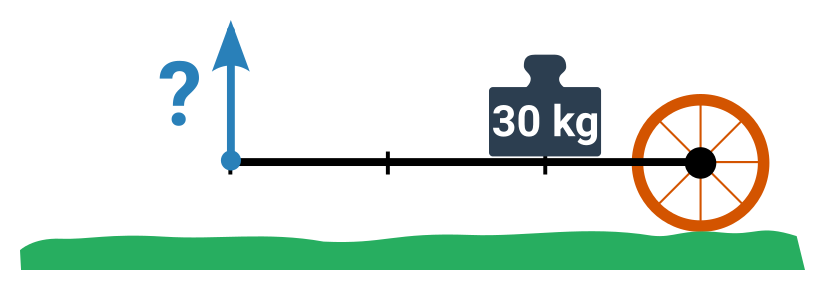
- Kombinujeme sílu a hmotnost. Musíme tedy nejprve převést hmotnost trakaře na tíhovou sílu.
- 30 kg znamená tíhovou sílu 300 N.
- Platí F_1:F_2=r_2:r_1 – síly musí mít opačný poměr než vzdálenosti do osy.
- Poměr vzdáleností r_2:r_1 je 3 ku 1. Tedy zvedáme trakař v trojnásobné vzdálenosti od osy.
- Poměr sil tedy bude 1 ku 3. Bude tedy stačit třetinová síla (vůči těm 300 N).
- Zvedat musíme silou 100 N.
Druh páky
Pokud působí všechny síly na jedné straně od osy otáčení jde o jednozvratnou páku (osa otáčení je pak obvykle na kraji, např. pinzeta, trakař). Pokud působíme silami na opačných stranách od osy otáčení, jde o dvojzvratnou páku (např. kleště, nůžky, houpačka).
Proč platí podobné vztahy pro hmotnosti i síly?
- Díky přímé úměře tíhy závaží a hmotnosti (F=m g).
- Konstanta g je pro všechna závaží stejná.
- Dosadíme za F_1 a F_2 do rovnice F_1:F_2=r_2:r_1.
- Dostaneme (m_1g):(m_2g)=r_2:r_1.
- Protože m_1g:m_2g je vlastně zlomek, můžeme v něm krátit konstantu g.
- Dostaneme m_1:m_2=r_2:r_1.
Kladka je v podstatě upevněné nebo zavěšené kolečko, které pomocí lanka nese nějaký náklad. Systém kladek se nazývá kladkostroj. Kladky dělíme na pevné (1) a volné (2).
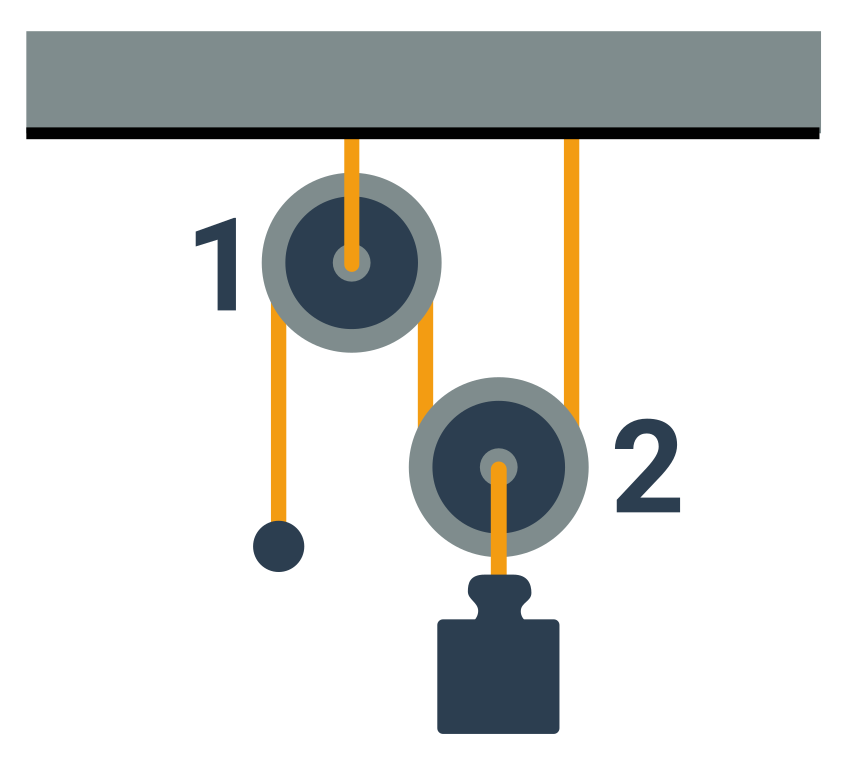
Pevná kladka se nemůže při zatáhnutí za lano hýbat. Volná se naopak bude pohybovat nahoru a dolů podle toho, jak se lanko, které ji nese, zkracuje či prodlužuje.
Kladky a kladkostroje fungují podobně jako páky (tedy umožňují unést těžký náklad pomocí malé síly). Navíc ale přidávají přenos směru síly. Tedy (otočením lanka přes kolečko) umožňují např. zvedat kyblík pomocí síly směřující dolů. Nebo šikmo.
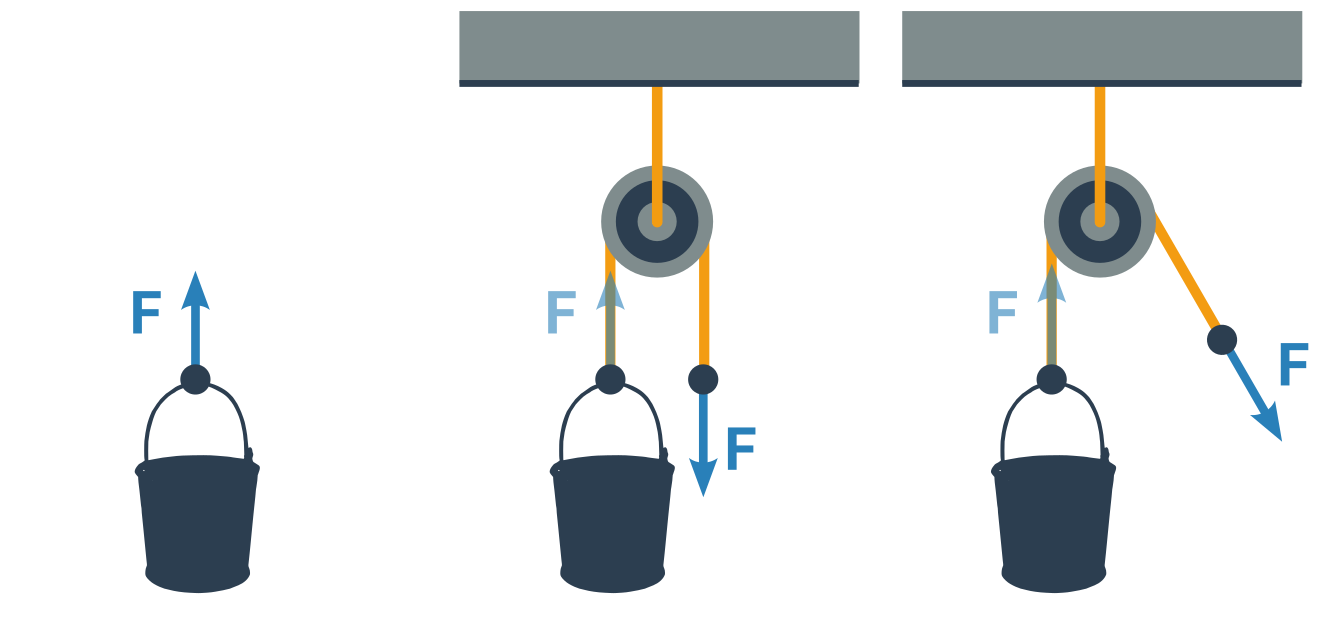
Pevná kladka
Otáčí se na ose v pevné konstrukci, nebo je osa zavěšena na laně, které má neměnnou délku.
Kolečko kladky je vlastně rovnoramenná páka. Obě vzdálenosti od osy jsou stejné a proto je velikost síly na obou stranách kolečka v rovnováze stejná. Pevná kladka tedy pouze přenáší směr síly po laně.
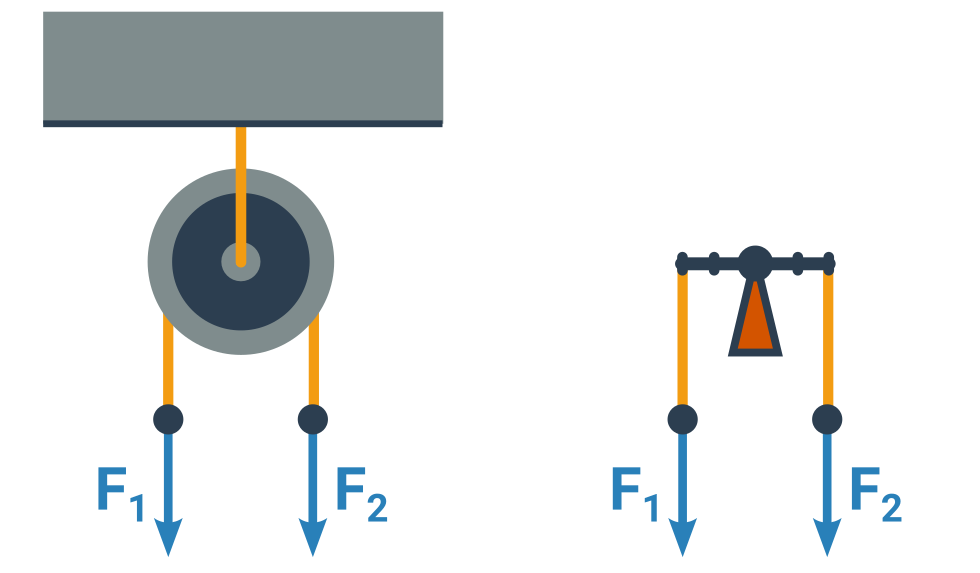
Volná kladka
Kladka zavěšená na pohyblivém laně funguje také jako páka, takže síly, které ji z obou stran táhnou nahoru, musí být stejné. Zároveň ale v rovnováze musí viset ve vzduchu a nepadat. Součet těchto sil tedy musí být stejný jako tíha, kterou kladka nese na své ose (aby výsledná síla byla 0).
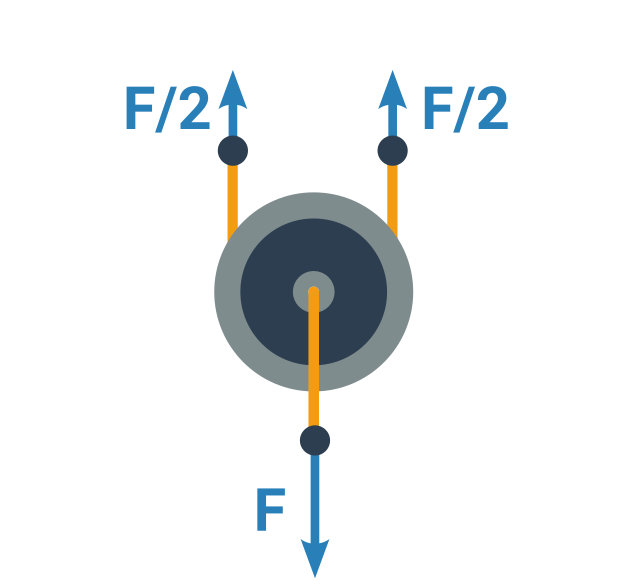
Každá volná kladka tedy zmenšuje sílu, kterou musíme za jeden konec lanka tahat, na polovinu.
Příklad: Síly na volné kladce
Nese volná kladka větší tíhovou sílu závaží, než kterou taháme za volný konec lana v drážce? (kladka se nehýbe)
- Podle obrázku výše musí být síly tahající za každý konec lana v drážce poloviční, než tíhová síla závaží.
- Na kladce tedy visí dvakrát tak síla, než kterou taháme.
- Odpověď je ano – tíhová síla je větší (dvojnásobná).
Příklad: Závaží na volné kladce
Obrázek ukazuje postup při zjištění síly, která drží kladku nahoře:
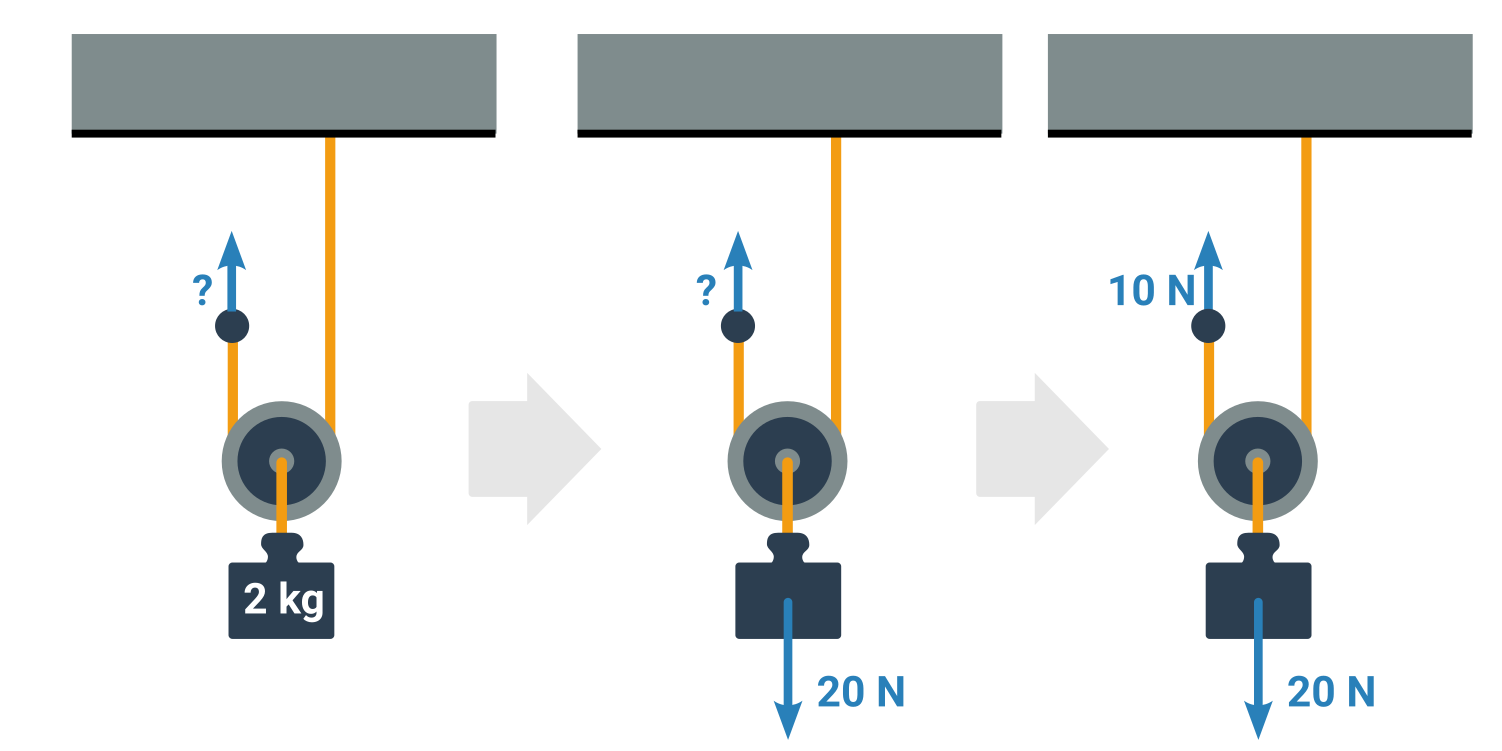
- Nejprve převedeme hmotnost závaží na tíhovou sílu. Stejnou silou musí ostatní lana kladku nést.
- Poté uplatníme pravidlo dělení sil nesoucích volnou kladku napůl.
- Vyjde nám 10 N.
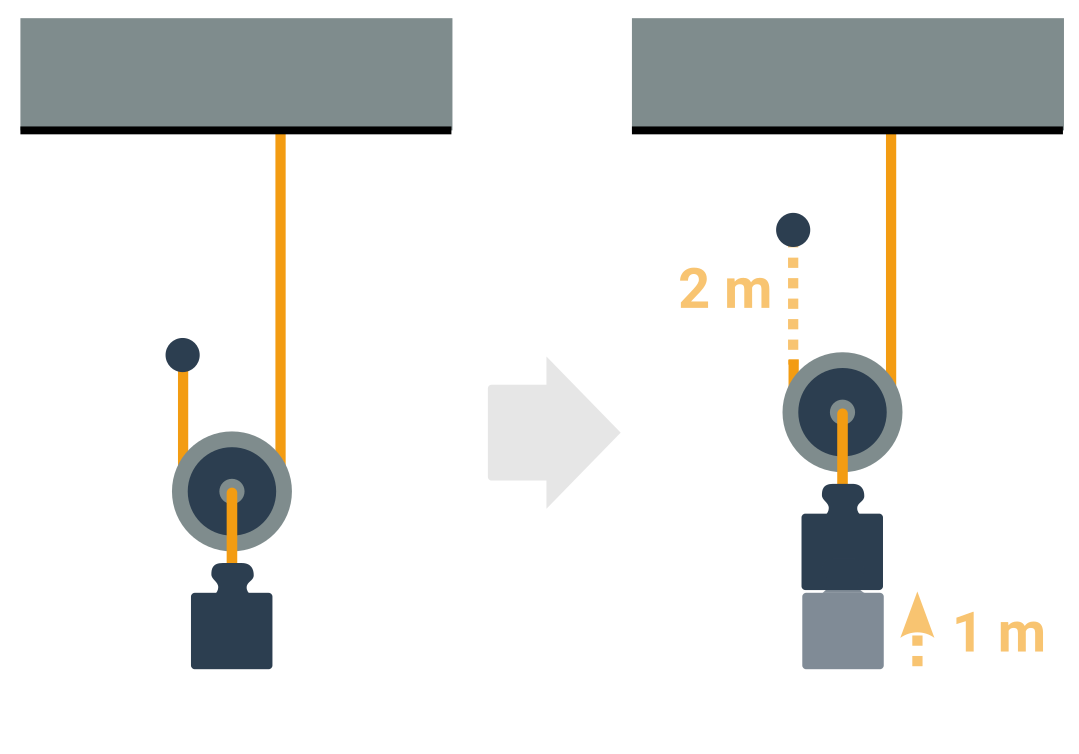
Zároveň ale pro zvednutí závaží na volné kladce o určitou výšku taháme dvojnásobnou délku lana (protože se musí zkrátit lano na obou stranách kolečka).
Kladkostroj
Je kombinace více kladek. Pokud rozložíme síly zátěže na volných kladkách, můžeme potřebnou sílu zmenšit i mnohonásobně.
Příklad: Závaží v kladkostroji
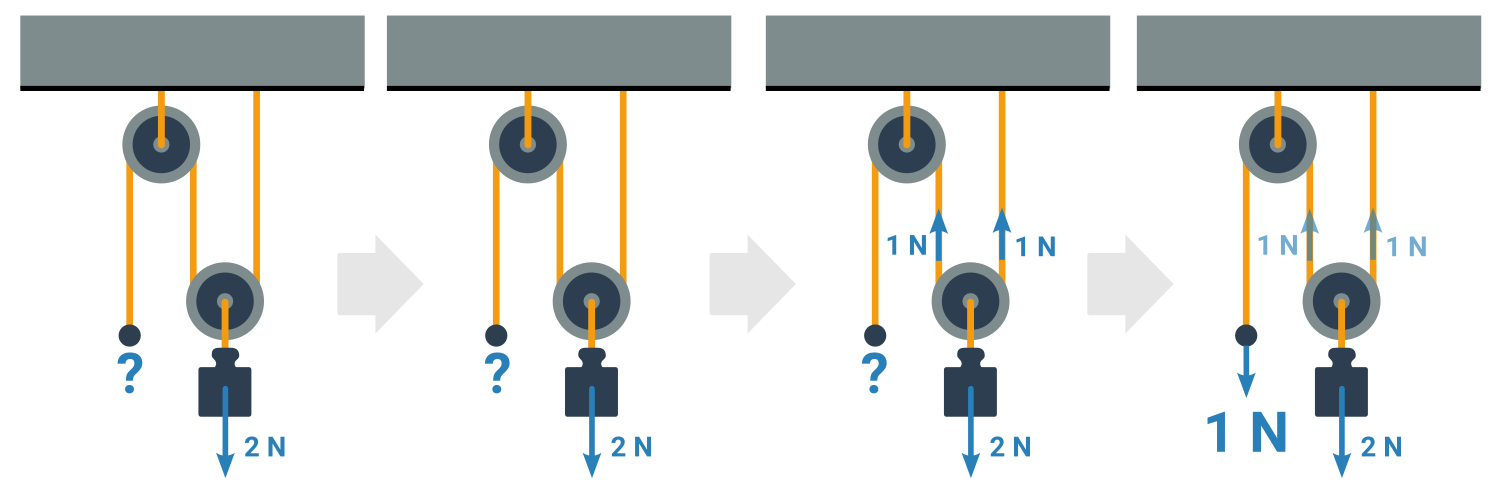


 Čeština
Čeština Matematika
Matematika Angličtina
Angličtina Informatika
Informatika Biologie
Biologie Němčina
Němčina Umíme to
Umíme to Zeměpis
Zeměpis Chemie
Chemie Dějepis
Dějepis Fyzika
Fyzika ZSV
ZSV
