
Deformace pevných látek

Normálové napětí \sigma_\mathrm{n}
Popisuje napětí v materiálu. Definujeme jej jako podíl síly F a průřezu tělesa S, na které síla působí.
\sigma_\mathrm{n} = \frac{F}{S}
V přeneseném významu odpovídá \sigma_\mathrm{n} tlaku, což naznačuje i pravá strana vzorce (shodná s obecnou definicí tlaku). I jednotkou je tedy pascal.
Hookův zákon
Když se deformací těleso prodlouží (nebo zkrátí), můžeme tu změnu popsat pomocí bezrozměrné veličiny relativní prodloužení \varepsilon. Tedy kolikanásobně se těleso prodlouží. Matematicky je to změna délky \Delta l děleno původní délka l_0 tělesa:
\varepsilon = \frac{\Delta l}{l_0}.
Příklad: Prodloužení tyče
Gumové lano jsme z původních 2 metrů natáhli na 2,4 m. Jaké je \varepsilon?
- Původní délka l_0 je 2 m.
- Změna délky \Delta l je rozdíl mezi 2,4 m a 2 m. Tedy 0,4 m.
- Dosadíme do \varepsilon = \frac{\Delta l}{l_0}=\mathrm{\frac{0{,}4\,m}{2\,m}}=0{,}2
- Relativní prodloužení je tedy 0,2 (nebo také 20 procent).
Hookův zákon udává, že normálové napětí \sigma_\mathrm{n} je přímo úměrné tomuto relativnímu prodloužení. Tedy:
\sigma_\mathrm{n} = E\cdot\varepsilon
Konstanta úměrnosti E je tzv. Youngův modul pružnosti (jednotka pascal). Hookův zákon ale platí jen pro menší normálová napětí (po mez úměrnosti \sigma_\mathrm{u}).
Příklad: Napětí v ocelové tyči
Jaké je napětí v ocelové tyči s E=200\,\mathrm{GPa}, když se kvůli němu prodloužila o desetinu své původní délky?
- Relativní prodloužení \varepsilon je desetina, tedy 0,1.
- E máme zadáno, to je 200 GPa, tedy 200 miliard Pa.
- Dosadíme do \sigma_\mathrm{n} = E\cdot\varepsilon
- Dostaneme 200 miliard krát 0,1.
- Napětí v tyči \sigma_\mathrm{n} je tedy 20 miliard Pascalů.
Jak na relativní prodloužení lana se znalostí působící síly?
Známe velikost působící síly F, materiál tělesa (tedy i modul pružnosti v tahu) a průřez materiálu S, jak se lano prodlouží?
- Využijeme definice normálového napětí (\sigma_\mathrm{p} = \frac{F}{S}) i Hookova zákona (\sigma_\mathrm{p} = E\cdot\varepsilon), dosadíme za \sigma_\mathrm{p}, potom \frac{F}{S} = E\cdot\varepsilon.
- Obě dvě strany podělíme modulem pružnosti E a obdržíme hledaný výsledek \varepsilon = \frac{F}{S\cdot E}.
Deformace pevné látky popisuje tzv. křivka deformace 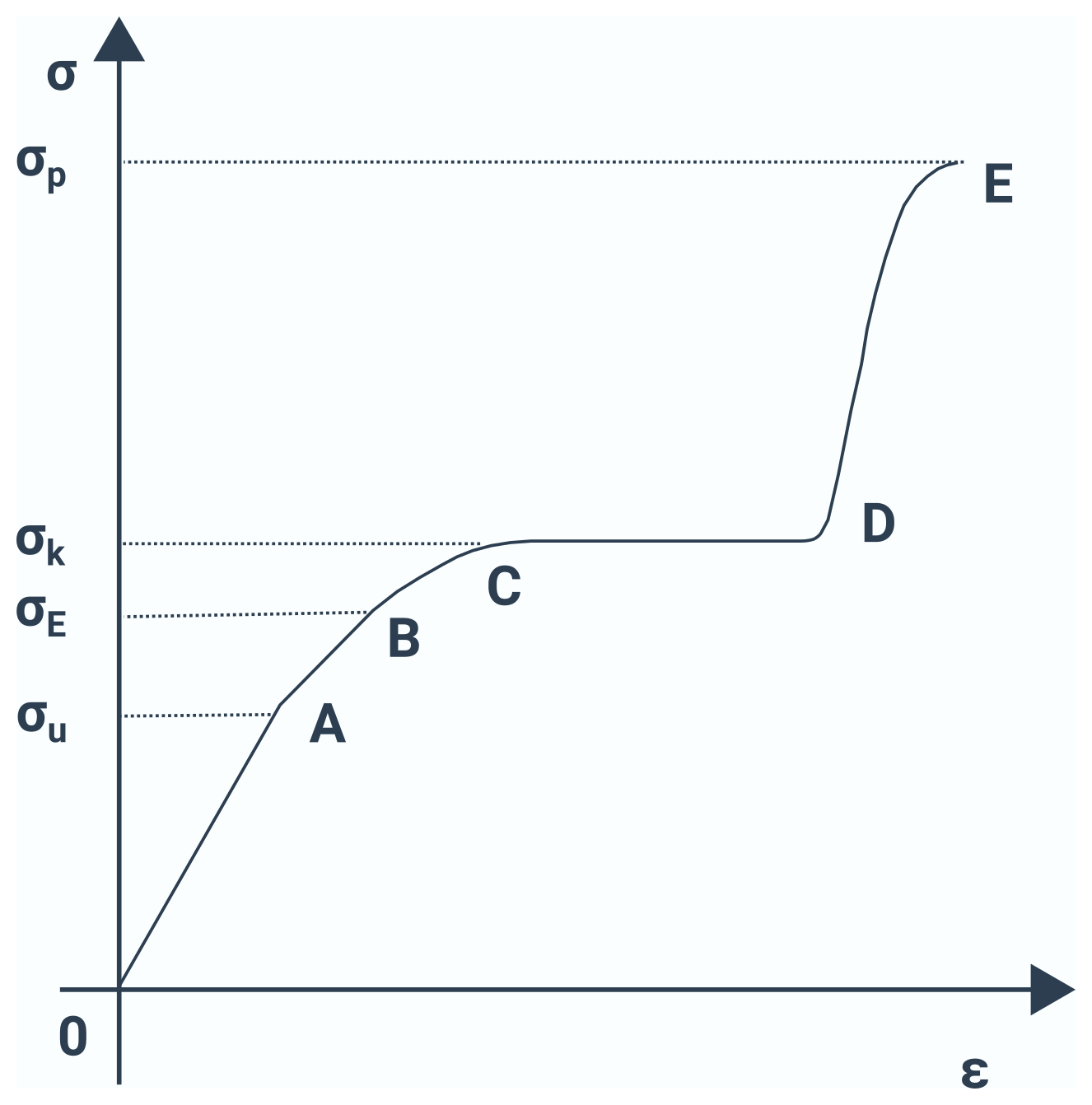 na křivce se nachází několik charakteristických bodů a intervalů
na křivce se nachází několik charakteristických bodů a intervalů
- 0B – pružná deformace (\sigma_\mathrm{u} je mez platnosti Hookova zákona a \sigma_\mathrm{E} mez pružnosti)
- BC – nepružná deformace (\sigma_\mathrm{k} je mez kluzu)
- CD – tečení materiálu
- DE – zpevnění
- oblast za E – těleso již nedrží pohromadě (\sigma_\mathrm{p} je mez pevnosti)
Zavřít


















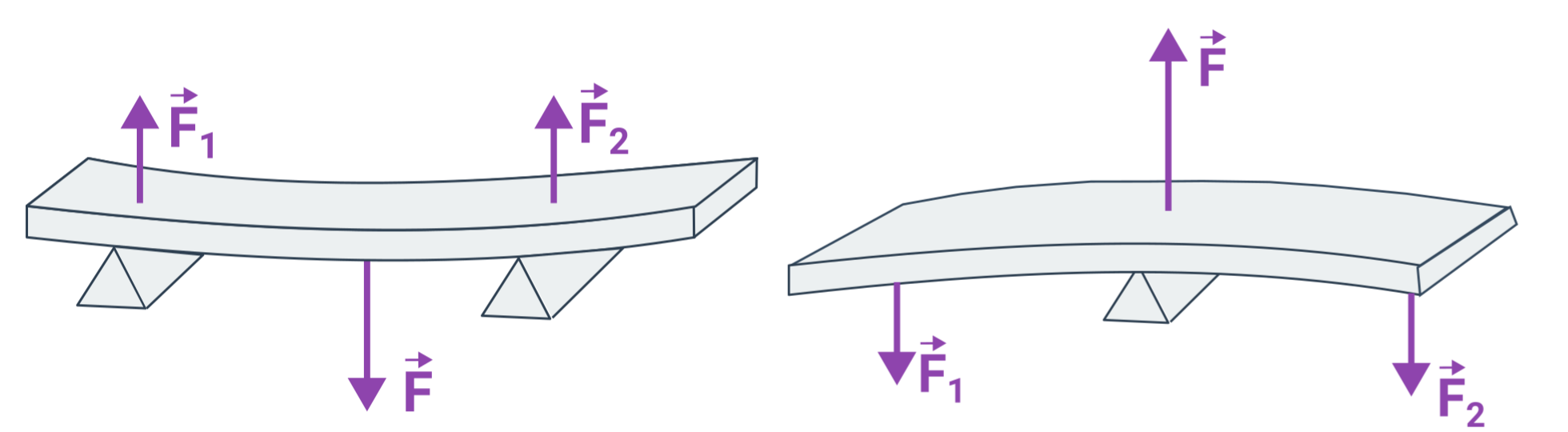
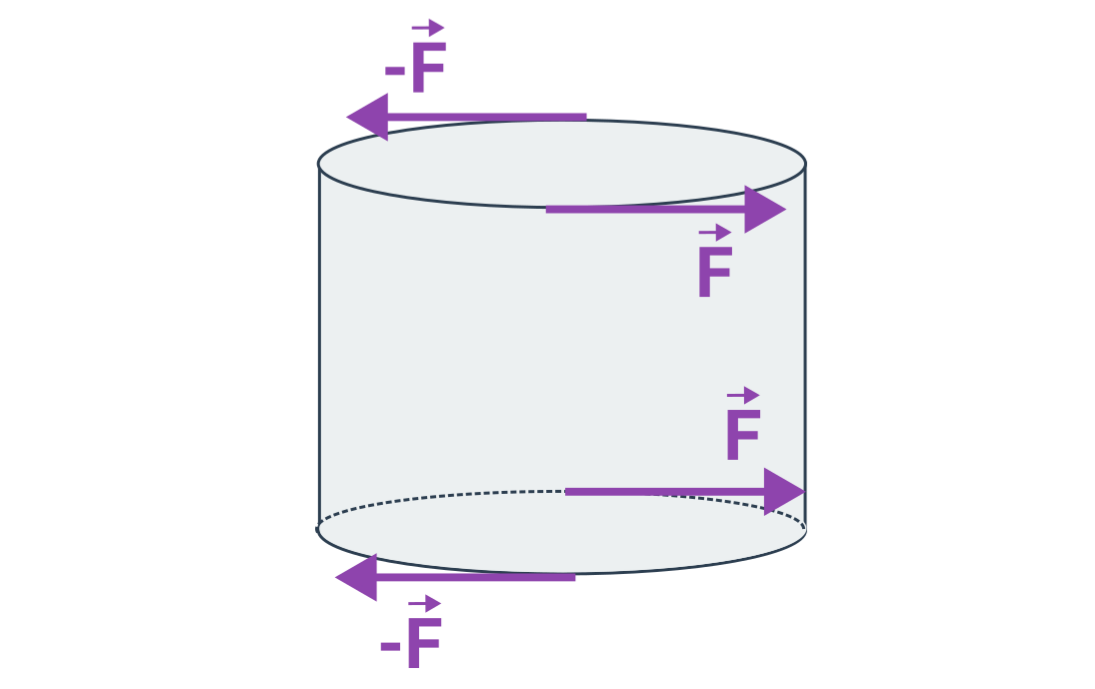
 na křivce se nachází několik charakteristických bodů a intervalů
na křivce se nachází několik charakteristických bodů a intervalů