Výpis souhrnů
Mechanika
Podtémata
- Kinematika (popis pohybu)
- Kinematika: základní pojmy
- Rychlost, dráha, čas
- Rychlost, dráha, čas: vzorce
- Rychlost, dráha, čas: pohyb tělesa
- Rychlost, dráha, čas: vzájemný pohyb těles
- Rovnoměrný a nerovnoměrný pohyb
- Zrychlení
- Dráha zrychleného pohybu
- Grafy pohybu
- Typy grafů pohybu
- Grafy polohy/dráhy: základy
- Grafy polohy/dráhy: odečítání údajů
- Grafy rychlosti: základy
- Grafy rychlosti: odečítání údajů
- Výpočty rychlosti a dráhy z grafů
- Vrhy a pády
- Poznávání vrhů
- Vlastnosti vrhů
- Volný pád
- Pohyb po kružnici
- Dynamika (příčiny pohybu)
- Skládání sil
- Newtonovy pohybové zákony
- Zákon setrvačnosti
- Zákon síly: se vztahy
- Zákon akce a reakce
- Typy sil
- Newtonův gravitační zákon
- Gravitační vs. tíhová síla a tíha
- Tlak a tlaková síla
- Smykové tření: základy
- Smykové tření: se vzorci a třecí silou
- Hybnost
- Moment síly
- Práce, výkon, energie
- Kinetická a potenciální energie
- Mechanická energie tělesa a soustavy těles
- Zákon zachování mechanické energie
- Práce
- Výkon: základy
- Výkon síly konající práci
- Účinnost a příkon
- Páky
- Kladky
- Mechanika kapalin a plynů
- Hydrostatický tlak: základy
- Archimédův zákon: intuitivně
- Atmosférický tlak
- Rovnice kontinuity
- Bernoulliho rovnice
- Vytékání kapaliny malým otvorem
- Deformace pevných látek
- Vlnění: pojmy
- Zvuk: základy
- Vlastnosti zvuku
- Rychlost zvuku a šíření zvuku
- Ultrazvuk, infrazvuk a sluch
- Zvuk v hudebních nástrojích
Kinematika (popis pohybu)
Je částí mechaniky, jejímž úkolem je popsat pohyb. Popisovat můžeme pohyb jednotlivých objektů, pohyb souboru objektů, pohyb tekutin a tak dále. V první části se ovšem převážně zaměřujeme na popis pohybu pevných těles.
Kinematika se nesnaží pohyb vysvětlit (proč se něco hýbe), to je podstatou dynamiky. Kinematika se jen ptá, jak se objekty pohybují prostorem:
Rovně?
Do zatáčky?
Stále stejně?
Čím dál tím rychleji?
Kinematika: základní pojmy
V mechanice se pohybují především různé objekty, tzv. tělesa. Často je zjednodušujeme na hmotné body (neuvažujeme rozměry a rotaci tělesa, jen hmotnost).

Křivku vykreslující kudy pohyb procházel nazýváme trajektorie. Její délka se nazývá dráha.
Popisovat pohyb můžeme z několika úhlů pohledu:
Jak se na pohyb díváme?
Pohyb musíme popisovat vůči něčemu. Proto zavádíme vztažné soustavy, tedy body vůči kterým poměřujeme svět a změny v něm. Obvykle je vztažná soustava určena počátečním bodem a souřadnicovými osami. Z různých vztažných soustav bude stejný pohyb vypadat jinak:

Speciálním případem je inerciální vztažná soustava, která nezrychluje a nezatáčí (nepociťujeme v ní setrvačné síly jako např. v brzdícím autobuse). Inerciální soustavy se vůči sobě pohybují stále stejným směrem a stejně rychle.
Jak pohyb vypadá?
Podle tvaru trajektorie rozdělujeme pohyby na přímočaré (pohybuje se stále rovně) a křivočaré (zatáčí).

U těles také rozlišujeme, jestli se někam posouvá, nebo se točí. Nebo obojí. Porovnáním trajektorií jednotlivých bodů tělesa tedy rozlišíme pohyb posuvný (translační) a otáčivý (rotační), případně složený.

Jak pohyb probíhá?
Z tvaru trajektorie zjistíme kudy se někdo pohyboval, ale už ne jak rychle. Stejnou zatáčku na polní cestě může opsat šnek i auto. Veličinou, která tyto pohyby odlišuje, je rychlost. Značíme ji v a je rovna dráze dělené časem t. Je buď průměrná (tedy podíl dráhy a času za nějakou dlouhou dobu) nebo okamžitá (změny dráhy za malou změnu času).
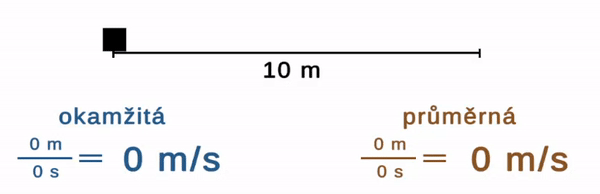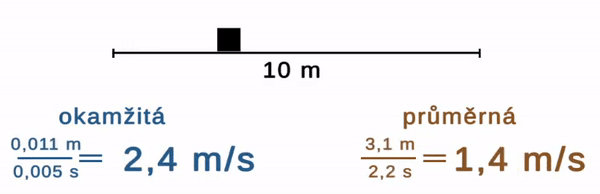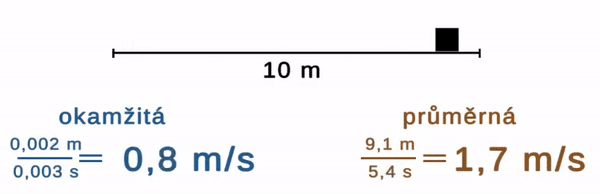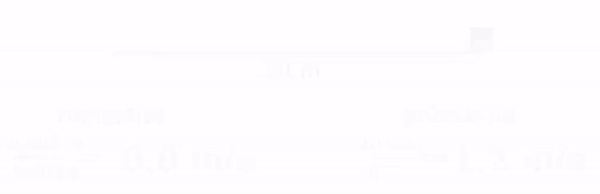
Pokud je rychlost stále stejně velká, mluvíme o rovnoměrném pohybu. Pokud se mění, jde o pohyb nerovnoměrný.

Jaký je tedy pohyb?
Výše zmíněné vlastnosti pohybu se různě kombinují, můžeme mít posuvný pohyb rovnoměrný a přímočarý, posuvný pohyb nerovnoměrný a přímočarý, rovnoměrný otáčivý pohyb a tak dále.
Zajímavosti
Inerciální soustava ve skutečnosti prakticky neexistuje. Vždyť i Sluneční soustava obíhá okolo galaktického jádra (a nepohybuje se tedy rovnoměrně přímočaře). Jsou jen soustavy, které jsou blíže k tomuto ideálu než jiné.
Rychlost, dráha, čas
Vztah mezi rovnoměrnou (nebo alespoň průměrnou) rychlostí v drahou s a časem pohybu t popisují vzorce:
v=\frac{s}{t}
s=v\cdot t
t=\frac{s}{v}
V jednoduchých případech pouze určíme správný vzorec a dosadíme.
U mnoha pohybů těles ovšem před dosazením musíme udělat něco navíc, např. převést správně jednotky nebo určit s ze změny poloh.
Konečně můžeme pomocí těchto vztahů také řešit vzájemný pohyb více těles.
Vztahový trojúhelník (pyramida)
Pokud známe nějaký vzorec typu \bf{A=B\cdot C} nebo \bf{A=B/C} (například v=s/t) můžeme pomocí jednoduché pomůcky zjistit, jak vypadají vzorce pro \bf{B} a pro \bf{C}.
- Nakreslíme si trojúhelníkovou pyramidu (zatím prázdnou).
- Zakreslíme do ní pravou stranu rovnice (naše s/t), tak aby vypadala graficky stejně jako ve vzorci (dělení jako zlomek nad sebou, případně násobení vedle sebe v dolním patře).
- Na zbývající místo doplníme levou stranu vzorce.

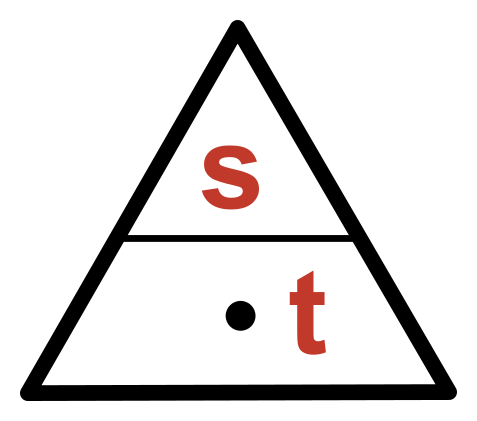
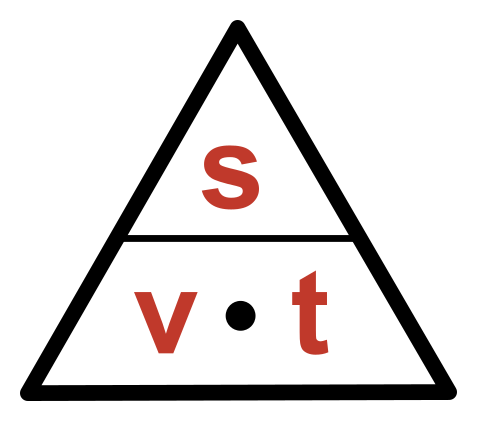
- Nyní stačí pro výpočet jakékoliv veličiny zakrýt tuto veličinu prstem a podívat se jak vypadají ostatní nezakryté.
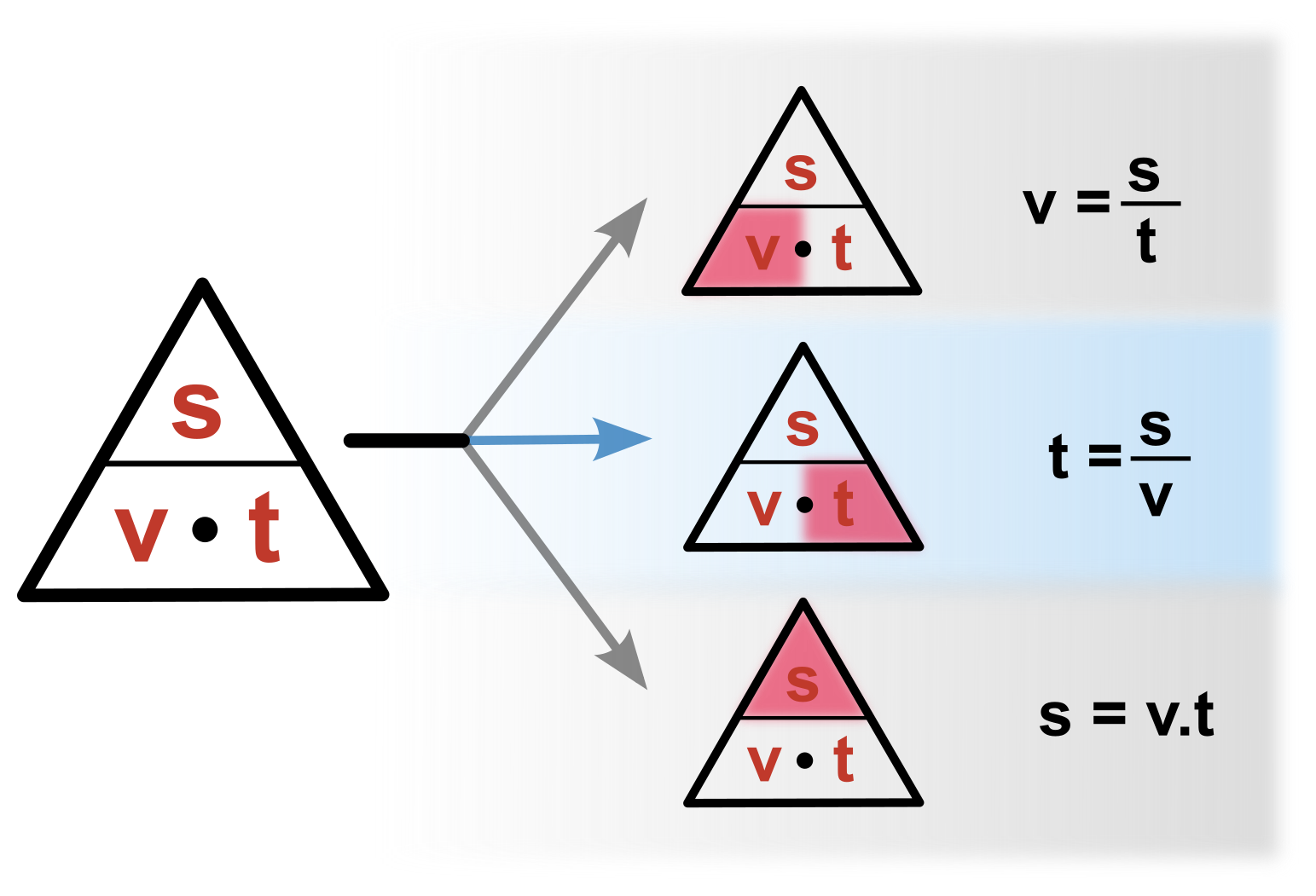
Rychlost, dráha, čas: vzorce
Definice rychlosti v je dráha s za čas t. Matematicky zapsáno je to
v=\frac{s}{t}
Jde vlastně o rychlost průměrnou, ale v případě rovnoměrného pohybu i o okamžitou rychlost po celou dobu pohybu.
Příklad: Rychlost auta
- Auto ujelo 200 km za 4 h. Jakou udržovalo rychlost?
- Hledáme v a známe s a t. Použijeme tedy vzorec v=\frac{s}{t}
- Dosadíme do něj za s a t.
- v=\frac{200}{4}\,\mathrm {km/h}=50\,\mathrm {km/h}
- Auto udržovalo rychlost 50 km/h.
Můžeme počítat i s a t (vždy když známe zbývající dvě veličiny). Matematickou úpravou, resp. použitím vztahového trojúhelníku jsme odvodili vztahy pro dráhu
s=v\cdot t
Příklad: Dráha Tarzana
- Tarzan na liáně letí rychlostí 12 m/s po dobu 5 s než se rozplácne o strom. Jakou dráhu uletěl?
- Hledáme s a známe v a t. Použijeme tedy vzorec s=v\cdot t.
- Dosadíme za v a t.
- s=12 \cdot 5\,\mathrm m=60\,\mathrm m
- Tarzan se rozplácl po 60 m.
a pro čas
t=\frac{s}{v}.
Příklad: Letové hodiny stíhačky
- Stíhačka přeletěla 800 km rychlostí 1600 km/h. Jak dlouho letěla?
- Hledáme t a známe s a v. Použijeme tedy vzorec t=\frac{s}{v}
- Dosadíme do něj za s a v.
- t=\frac{800}{1600}\,\mathrm h=0{,}5\,\mathrm h
- Stíhačka letěla půl hodiny.
Rychlost, dráha, čas: pohyb tělesa
Ne vždy můžeme ihned dosadit do vzorců jako s=v\cdot t. Musíme totiž nejprve vyřešit drobné komplikace:
- Jednotky nesedí. Musíme převést na stejné jednotky, nebo alespoň tak abychom nekombinovali různé časové škály (např km/h se sekundami)
Autobus
- Autobus jel 15 minut rychlostí 40 km/h. Kolik toho ujel?
- V jednotce rychlosti jsou hodiny zatímco čas je v minutách. Musíme tedy převádět.
- Mohli bychom převádět na m/s a sekundy, ale bylo by to pracné.
- Lepší je převést čas na hodiny (výsledek vyjde v km).
- 15 minut → 0,25 h
- Konečně můžeme dosadit do s=v\cdot t.
- s=40\cdot 0{,}25 \,\mathrm{km} = 10\,\mathrm{km}
- Dráhy/časy složené z více částí. Celková dráha pohybu s je prostě součtem drah všech úseků s=s_1+s_2+\cdots. Totéž platí pro čas t=t_1+t_2+\cdots.
Triatlon
- Triatlonista zvládl závod za 2h. Přitom ujel 40 km na kole, 10 km běžel a 1,5 km plaval. Jakou měl průměrnou rychlost během celého závodu?
- Použijeme vzorec v=\frac{s}{t}, ale přímo známe jen čas t. Potřebujeme s.
- Celková dráha s je podle s=s_1+s_2+s_3
- Číselně s=40+10+1{,}5\,\mathrm {km}= 51{,}5\,\mathrm {km}.
- Už můžeme dosazovat v=\frac{51{,}5}{2}\,\mathrm {km/h}=25{,}75\,\mathrm {km/h}
Pro rychlost to ale neplatí! Průměrná rychlost více úseků dohromady se musí počítat jako v=\frac{s_1+s_2+\cdots}{t_1+t_2+\cdots}.
- Místo dráhy/času známe jen hodnoty na začátku a na konci. Neznáme dráhu přímo, ale známe polohy na trati na začátku a na konci pohybu. Podobně může být potřeba určit dobu pohybu t jako rozdíl časů (na hodinách) v okamžiku startu a cíle.
Sjezdy na dálnici
- Na dálnici jsme najeli nájezdem na 20. km a opustili ji sjezdem na 200. km. Jak dlouho jsme na ní strávili s rychlostí 90 km/h?
- Hledáme t. Přímo známe ale jen v.
- Dráhu s musíme určit jako rozdíl poloh na začátku a na konci.
- s=200-20\,\mathrm{km}=180\,\mathrm{km}
- Teprve nyní můžeme dosadit do t=\frac{s}{v}.
- t=\frac{180}{90}\,\mathrm{h}=2\,\mathrm{h}
Rychlost, dráha, čas: vzájemný pohyb těles
Pokud se pohybuje více těles, můžeme zkoumat jejich vzájemný pohyb.
Vzájemná rychlost dvou těles (těleso 1 a těleso 2) je rozdílem jejich rychlostí. Pokud budeme jednotlivé rychlosti značit indexy, můžeme pro vzájemnou rychlost použít v.
v=v_1-v_2
(pokud je důležitý směr a pokud rozlišujeme, zda jde o rychlost 1. tělesa vůči 2. nebo naopak, používá se také v_{12} resp v_{21})
Pokud se k sobě tělesa přibližují, určuje vzorec t=\frac{s}{v} čas setkání – dosazujeme do něj právě vzájemnou rychlost a počáteční vzdálenost těles (i pro tu používáme přímo písmeno s protože pro dráhy jednotlivých těles pravděpodobně použijeme s_1 a s_2).
Dráhy jednotlivých těles a místo setkání je možné poté dopočítat, když dosadíme do vzorce pohybu jednotlivých těles vypočtený čas setkání t (např. s_1=v_1\cdot t, nebo s_2=v_2\cdot t).
NahoruRovnoměrný a nerovnoměrný pohyb
Pohyb dělíme na rovnoměrný a nerovnoměrný podle toho, jestli se mění velikost rychlosti. U tohoto dělení naopak nezáleží na tom, jestli se mění směr pohybu (směr rychlosti).
rovnoměrný pohyb = velikost rychlosti je stále stejná, zrychlení je nulové, nebo kolmé na směr pohybu (pohyb po kružnici)
nerovnoměrný pohyb = velikost rychlosti se mění, zrychlení není nulové
Zrychlení
Pokud se rychlost pohybu mění, charakterizuje tyto změny veličina jménem zrychlení. Značíme jej a a je to změna rychlosti za změnu času.
a=\frac{\Delta v}{ \Delta t }
- Rychlost lodi vzrostla o 6 m/s během 3 s. Zrychlení bylo 2 m/s².
Jednotkou zrychlení je \mathrm{m/s^2}.
Zejména v kinematice můžeme zrychlení brát jako změnu velikosti rychlosti. Pokud je stále stejné, jde o pohyb rovnoměrně zrychlený nebo pohyb rovnoměrně zpomalený.
Pro rychlost rovnoměrně zrychleného pohybu platí:
v=v_0+a\cdot t nebo jednodušeji v=a\cdot t (pokud je počáteční rychlost v_0 nulová)
Vztah pro dráhu je pak:
s=v_0t+\frac{1}{2}a t^2 nebo jednodušeji s=\frac{1}{2}a t^2 (pokud je počáteční rychlost v_0 nulová)
V případě rovnoměrně zpomaleného pohybu (rychlost se rovnoměrně snižuje), používáme obvykle vztahy v=v_0-a\cdot t pro rychlost a s=v_0t-\frac{1}{2}a t^2 pro dráhu.
Zjednodušené vztahy (v_0=0) v tomto případě nemají smysl, protože musíme mít z čeho zpomalovat.
Zpomalení a záporné zrychlení
Je i alternativa používat pro zpomalený pohyb stejné vztahy jako pro pohyb zrychlený a dosazovat záporné hodnoty zrychlení a. V následujících cvičeních ale není použita.
Přesnější definice zrychlení je změna vektoru rychlosti za změnu času.
\vec a=\frac{\Delta \vec v}{ \Delta \vec t }
Zrychlení je podle této definice nenulové i u rovnoměrného pohybu po kružnici a každého křivočarého pohybu (mění se směr vektoru rychlosti).
NahoruDráha zrychleného pohybu
Graf závislosti rychlosti na čase u rovnoměrného pohybu vypadá takto:
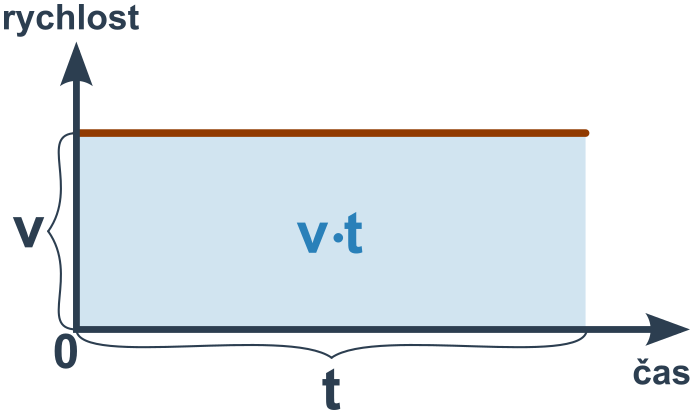
Plocha pod křivkou rychlosti má obsah v\cdot t (obsah obdélníka) což je přesně rovno dráze rovnoměrného pohybu. To platí obecně – obsah plochy pod křivkou rychlosti v grafu v/t je roven dráze.
U rovnoměrně zrychleného pohybu (konstantní a) nejde o obdélník, plocha je ale stejná jako plocha obdélníka o výšce průměrné rychlosti \bar v (plocha △ a △ je totiž stejná).
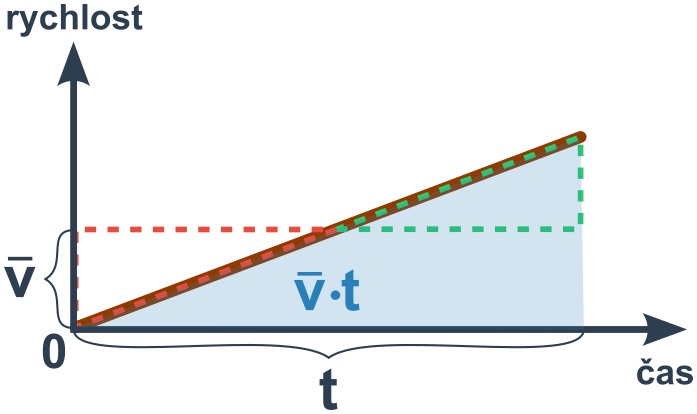
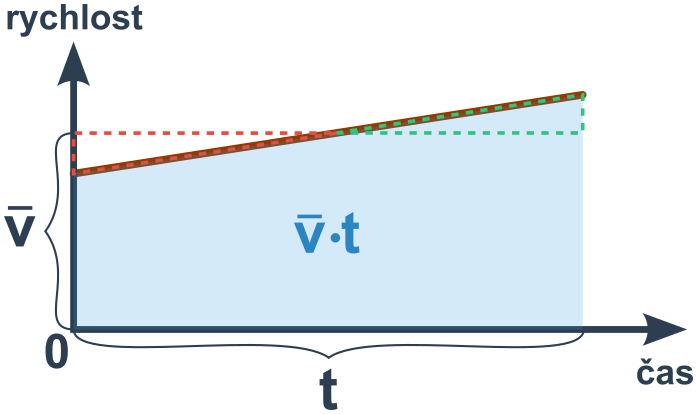
Dráhu rovnoměrně zrychleného pohybu počítáme v různých situacích:
Pohyb začíná z klidu
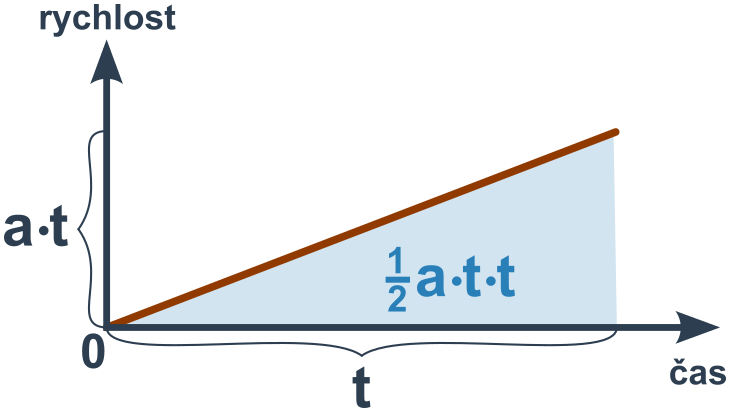
Pro rychlost platí v=a\cdot t (přímá úměra). Dráha (obsah pod křivkou) je rovna:
s=\frac{1}{2}at^2
Příklad: Dráha rozjíždějícího se auta
Auto se z klidu rozjíždí se zrychlením 2 m/s². Jakou dráhu ujede za 3 s?
- Zrychlení a je 2 m/s² a čas t je 3 s.
- Můžeme je přímo dosadit do s=\frac{1}{2}at^2.
- s=\frac{1}{2}at^2=\frac{1}{2}2\cdot 3^2\,\mathrm m=9\,\mathrm m
- Auto urazilo 9 m.
Příklad: Dráha valícího se kamene (grafická úvaha)
Na svahu se uvolnil kámen a začal se kutálet dolů se zrychlením 0,5 m/s². Jakou dráhu urazí za 10 s?
- Zrychlení a je 0,5 m/s² a čas t je 10 s.
- V grafu v-t je první odvěsna △ (vodorovná) rovna t, tedy 10 s.

- Druhá odvěsna je rovna a\cdot t, tedy 5 m/s– to je vlastně konečná rychlost v čase 10 s.
- Obsah △ je polovina součinu odvěsen. Tedy s=\frac{1}{2}\cdot 10\cdot 5\,\mathrm m=25\,\mathrm m
- Kámen tedy urazil 25 m.
Těleso se už pohybuje rychlostí v_0 a zrychluje
S nenulovou v_0 máme rychlost v=v_0+a\cdot t. Pak je dráha rovna součtu:
s=v_0\cdot t + \frac{1}{2}at^2
I to můžeme vyčíst z grafu (celková plocha = součet ▯ v_0\cdot t a △ \frac{1}{2}at^2):
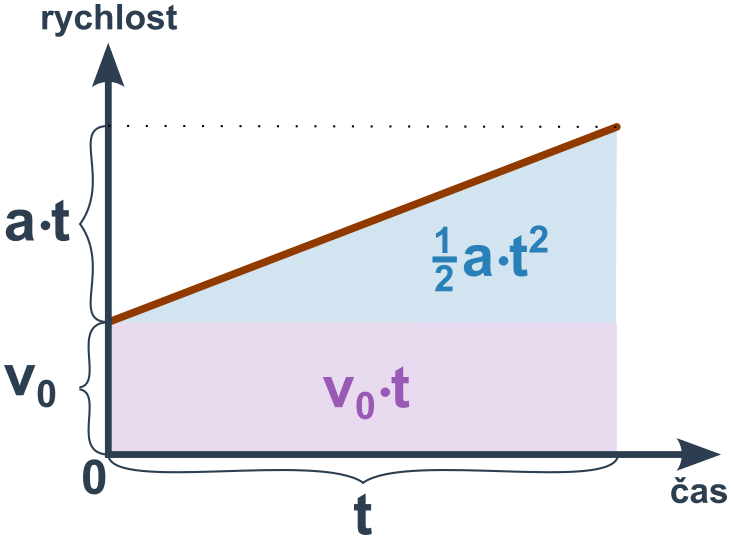
Příklad: Nástup závodníka do finiše
Závodník v cílové rovince z původní rychlosti 5 m/s rovnoměrně zrychloval (o 1 m/s²). Jak daleko byl cíl, pokud doběhl za 4 s?
- Zrychlení a je 1 m/s², čas t je 4 s a rychlost v_0 je 5 m/s.
- Můžeme je přímo dosadit do s=v_0\cdot t+\frac{1}{2}a t^2.
- s=v_0\cdot t+\frac{1}{2}at^2=5\cdot 4 + \frac{1}{2}1\cdot 4^2\,\mathrm m=20+8\,\mathrm m=28\,\mathrm m
- Když začal zrychlovat, byl závodník 28 m od cíle.
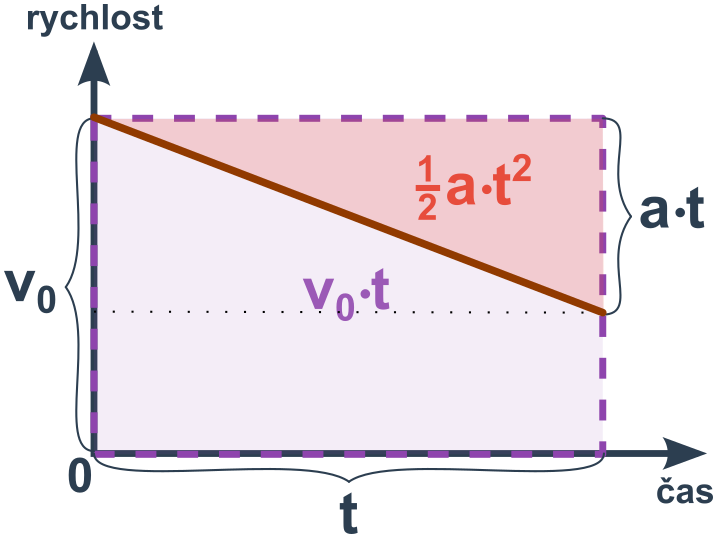
Těleso se už pohybuje rychlostí v_0 a zpomaluje
Platí totéž co v předchozím bodě, jen obsah △ odečítáme.
s=v_0\cdot t -\frac{1}{2}at^2
Příklad: Brzdění auta
Řidič plynule zpomaloval z 30 m/s po dobu 2 se zrychlením 5 m/s². Jakou dráhu urazil?
- Čas t je 2 s, rychlost v_0 je 30 m/s a zrychlení a je 5 m/s².
- Můžeme tedy přímo dosadit do s=v_0\cdot t-\frac{1}{2}a t^2.
- s=v_0\cdot t-\frac{1}{2}at^2=30\cdot 2 - \frac{1}{2}5\cdot 2^2\,\mathrm m=60-10\,\mathrm m=50\,\mathrm m
- Řidič během těch dvou sekund zpomalování urazil 50 m.
Grafy pohybu
Grafy pohybu jsou nejčastěji 2-D grafy, jak je známe z matematiky, které zobrazují vývoj nějaké veličiny popisující pohyb (y-ová, svislá osa) v závislosti na čase (x-ová, vodorovná osa).
Zobrazované veličiny jsou typicky poloha (na trati nebo dráze, obvykle nejde o skutečnou 3-D polohu), uražená dráha, nebo rychlost. Ale mohli bychom zobrazovat i např. zrychlení nebo jiné, obskurnější veličiny. Jde vlastně o záznam „měření“ dané veličiny v čase.
Z grafu pohybu můžeme:
- Zjistit typ grafu, o který se jedná (zaznamenaná veličina, počet těles, …).
- Získat základní informace o pohybu podle tvaru křivky v grafech. Jak v grafech polohy/dráhy, tak rychlosti.
- Odečítat hodnoty v grafech polohy i rychlosti v konkrétních bodech pohybu (např. v jakém čase byla rychlost nejvyšší).
- Vypočítat další veličiny (například rychlost z grafu dráhy nebo dráhu z grafu rychlosti).
Typy grafů pohybu
Rozlišujeme dva nejčastější typy grafů. Ty které zobrazují prostorovou veličinu (poloha, dráha) a ty které zobrazují rychlost. Poznáme to podle toho jak je označena svislá osa grafu. Kromě toho mohou existovat graf i jiných veličin (např. zrychlení), ale většinou je nepoužíváme.
Přitom jeden graf může zachycovat pohyb jednoho, ale i více těles (pak se v něm nachází více křivek, nebo sad bodů).
NahoruGrafy polohy/dráhy: základy
Grafy polohy (zde značíme x) a uražené dráhy (zde značíme s) jsou často vzájemně zaměnitelné, někdy ale ne. Dráha totiž narůstá i když se otočíme a začneme se po trase vracet. Poloha ne. Dráha navíc obvykle začíná na nule, což poloha nemusí. Ilustrují to následující grafy stejného pohybu dvou těles – jednou pro polohu, podruhé pro dráhu.
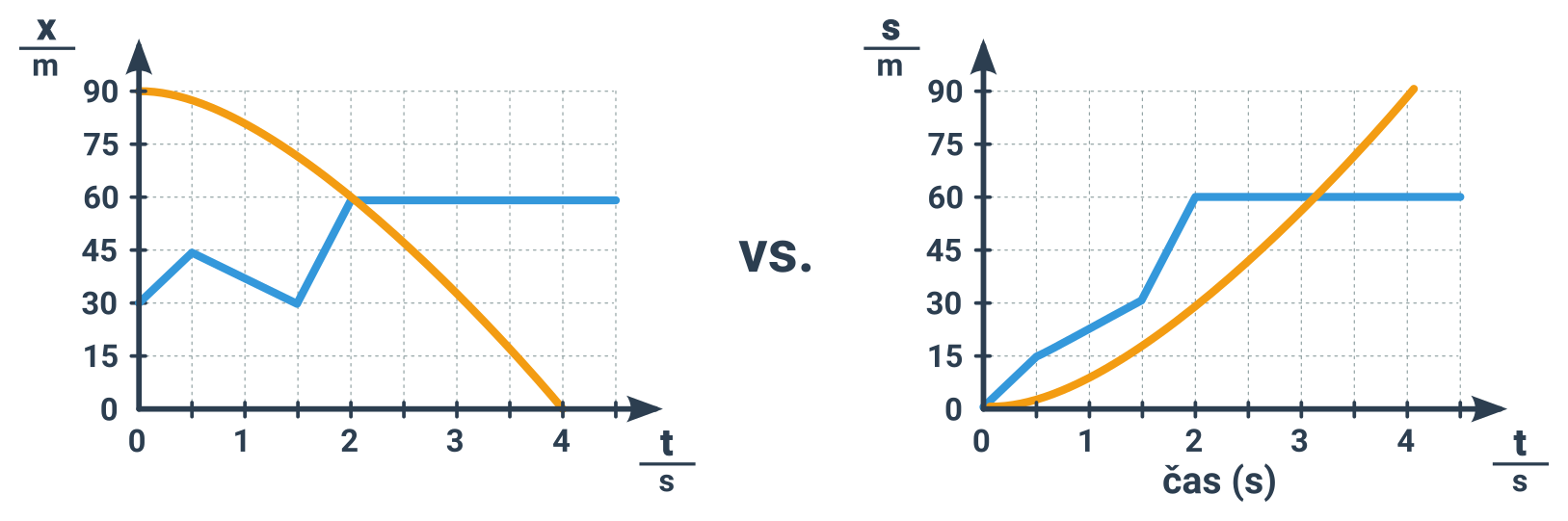
Platí, že čím strmější je křivka, tím rychlejší je pohyb. To znamená několik základních pouček pro kvalitativní pochopení zobrazeného pohybu:
- zlom křivky = náhlá změna rychlosti
- ohýbání křivky = plynulá změna rychlosti
- přímé úseky = rovnoměrný pohyb
- vodorovná část křivky = těleso stojí na místě
Příklad: Dráha auta a cyklisty
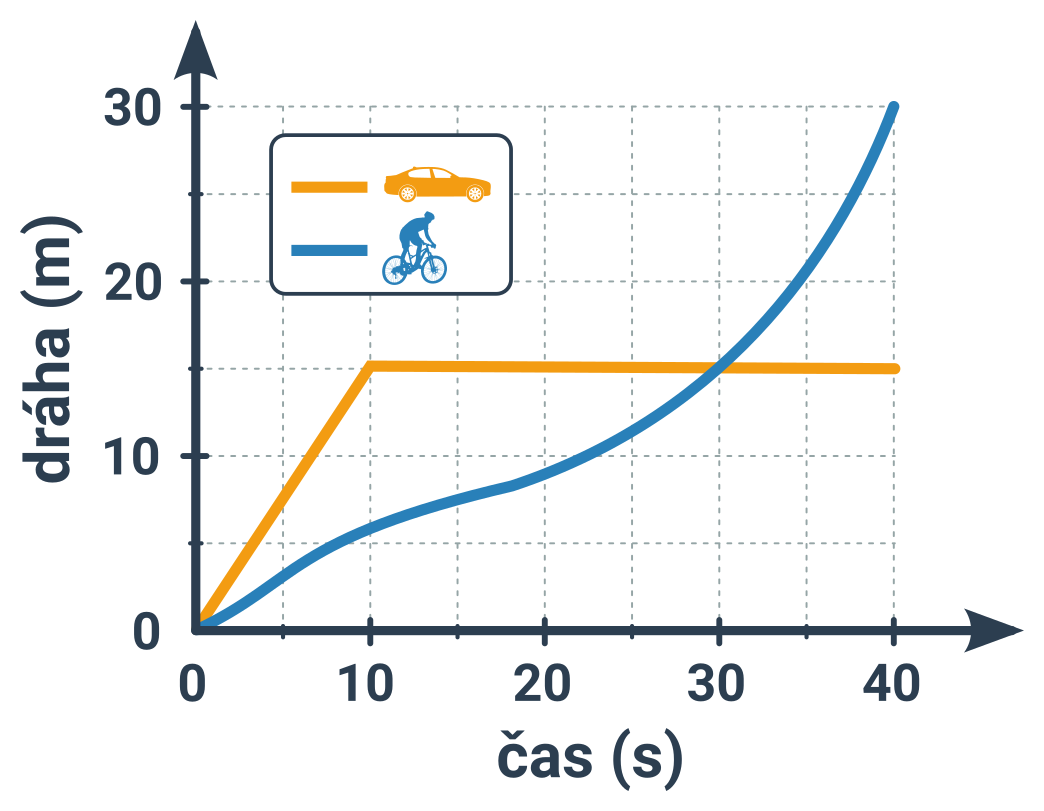
- Podle legendy je auto znázorněno oranžovou křivkou.
- Ta zpočátku (pravý kraj grafu) stoupá, auto se tedy pohybuje (dráha roste). A protože je tento úsek úsečka (nezakřivená), pohyb auta je tu rovnoměrný.
- Poté se křivka náhle zlomí do vodorovna. Auto tedy v mžiku změnilo rychlost na nulovou a stojí na místě. Až do konce (křivka je vodorovná až do konce grafu).
- Modrá křivka cyklisty je stále skloněná. Cyklista se tedy celou dobu pohybuje. Sklon se ale mění (nejde o úsečku). Jeho pohyb je tedy nerovnoměrný.
- Nejstrmější je křivka na konci, tehdy má tedy cyklista nejvyšší rychlost.
Grafy polohy/dráhy: odečítání údajů
Pro odečítání nějaké hodnoty z grafu existuje několik základních úkolů:
1. Máme daný bod na křivce a máme zjistit jeho souřadnici (časovou nebo polohovou/dráhovou).
Jednoduše z tohoto bodu vedeme kolmici na osu žádané veličiny. Poloha průsečíku pak odpovídá hledané hodnotě.
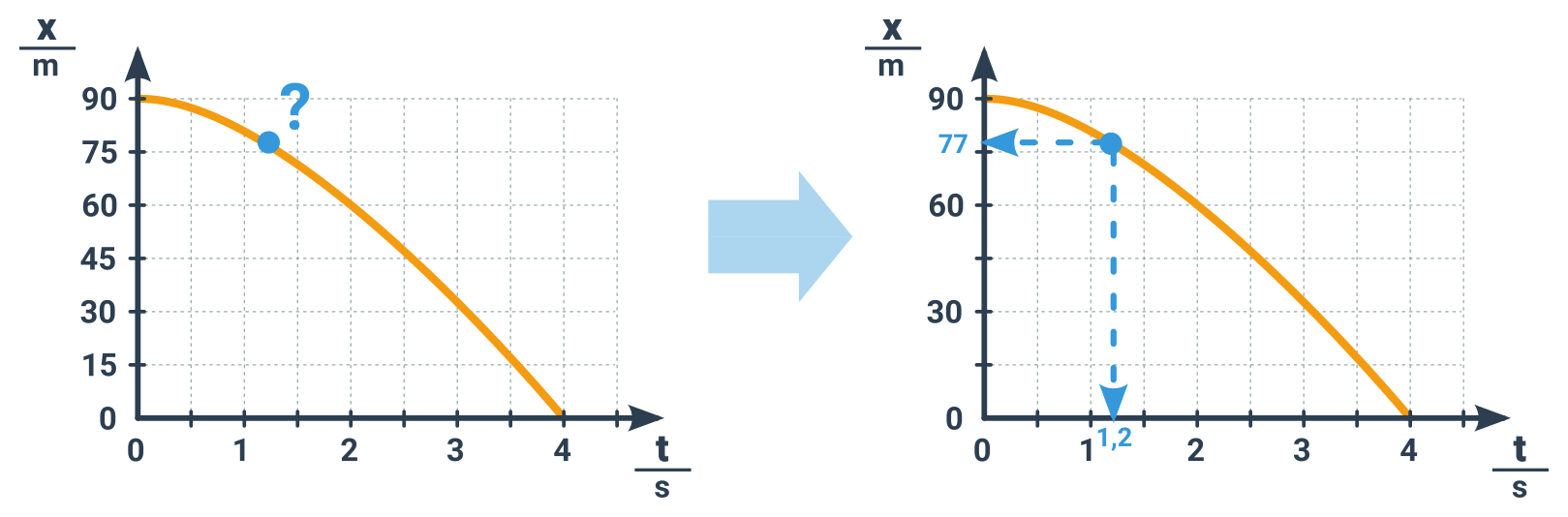
Nejčastěji když má samotný bod křivky nějaký význam, například zastavení tělesa (křivka se tam láme do vodorovna). Často jej tedy musíme nejprve identifikovat (můžete procvičit i zde)
Příklad: Poloha na konci
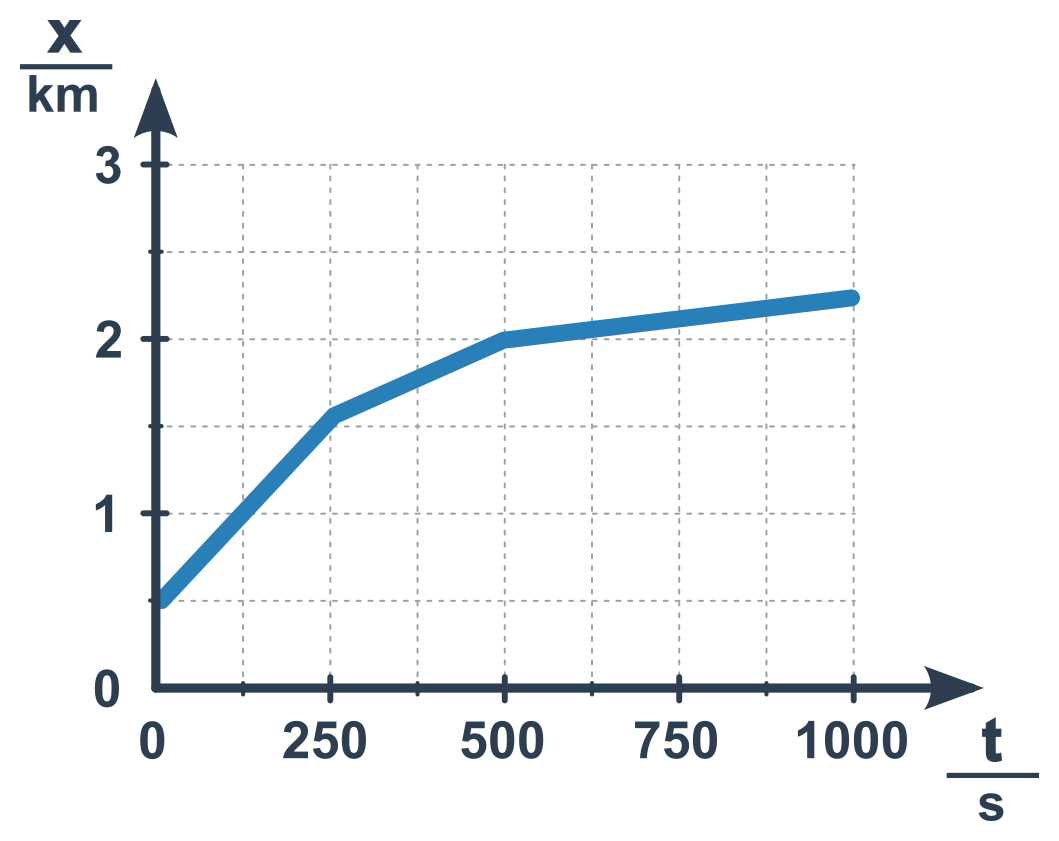
- Jakou polohu má těleso na konci sledování pohybu.
- Zjevně jde o bod na pravém konci křivky.
- Z tohoto bodu jedeme vodorovně doleva ke svislé ose.
- Protneme ji asi půl dílku nad 2. Velikost dílku je 0,5 km.
- Proto je poloha tělesa na konci 2 plus polovina z 0,5. Tedy 2,25 km.
2. Pro daný čas hledáme polohu/dráhu tělesa.
Vedeme z tohoto časového bodu kolmici. Hledáme průsečík s křivkou pohybu. Z něj vedeme kolmici na osu polohy podobně jako v bodu 1.
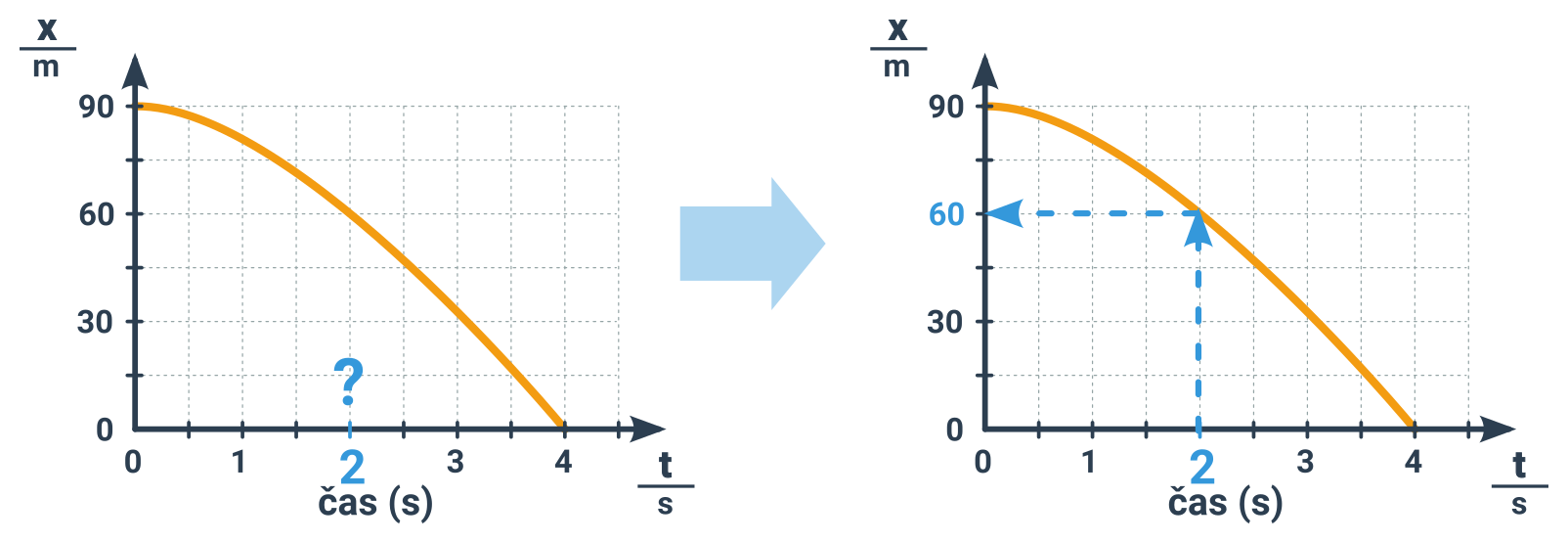
3. Pro určitou polohu/dráhu hledáme čas, kdy se na ni těleso nachází.
Postup je obdobný jako v bodě 2, jen začínáme ze svislé osy.
Ne vždy ale existuje řešení (průsečík s křivkou). Pak můžeme říct, že taková situace nenastane nikdy.
Příklad: Určení času při dosažení polohy 2 km

- Chceme znát čas, kdy je těleso na poloze 2 km.
- Najdeme na svislé ose 2 km a vedeme z ní vodorovnou čáru (zde už je naznačena mřížkou).
- Tam, kde se protne s křivkou pohybu, je náš bod. Je to přesně ve druhém zlomu křivky.
- Kolmo dolů pod tímto bodem dojdeme na časovou osu, na hodnotu 500 s.
Grafy rychlosti: základy
Grafy rychlosti zobrazují velikost rychlosti v čase. Nenesou informaci o poloze, byť uraženou dráhu z nich zjistit můžeme (čím větší plocha pod křivkou, tím větší uražená dráha). Z tvaru a polohy křivky můžeme určit některé kvalitativní vlastnosti pohybu:
- vodorovná část křivky na nule = těleso stojí na místě
- vodorovná část křivky = rovnoměrný pohyb
- přímé úseky (šikmo) = rovnoměrně zrychlený/zpomalený pohyb
- zakřivené úseky = nerovnoměrně zrychlený/zpomalený pohyb
Grafy rychlosti: odečítání údajů
Pro odečítání z grafů rychlosti platí to stejné jako pro odečítání údajů z grafů polohy a dráhy. Jen na svislé ose odečítáme rychlosti.
Řešíme tedy stejné tři úlohy – hledáme buď souřadnice bodu (který často musíme identifikovat), hodnotu rychlosti v daném čase, nebo čas, kdy má rychlost určitou hodnotu.
NahoruVýpočty rychlosti a dráhy z grafů
I z grafů dráhy/polohy můžeme určit rychlost a z grafů rychlosti dráhu. Ne vždy je to jednoduché udělat přesně, ale alespoň odhadnout je můžeme vždy.
Výpočet rychlosti z grafu polohy/dráhy
Můžeme určovat průměrnou rychlost celého pohybu (v=s/t) nebo nějakého jeho úseku (v=\Delta s/ \Delta t). Symbol \Delta značí rozdíl hodnot, např. \Delta t = t_\mathrm{konec}-t_\mathrm{zacatek}.
Odečteme údaje na osách pro oba krajní body úseku a dosadíme do výpočtu:
v=\frac{s_\mathrm{konec}-s_\mathrm{zacatek}}{t_\mathrm{konec}-t_\mathrm{zacatek}}
Příklad: Celková průměrná rychlost pohybu se změnou rychlosti
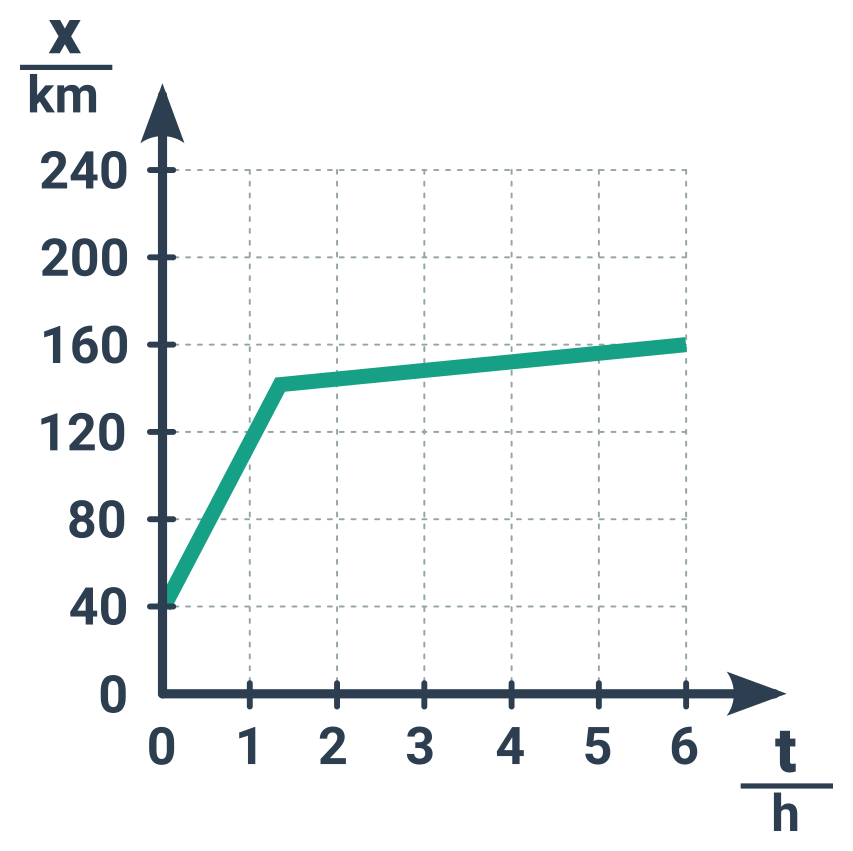
Dosadíme krajní hodnoty do vzorce (160 km a 40 km do čitatele, 6 h a 0 h do jmenovatele) a dostaneme průměrnou rychlost

Výpočet dráhy z grafu rychlosti
V grafu rychlosti tělesa je dráha vlastně obsahem plochy pod křivkou rychlosti. Obecně je to těžké. Někdy jsou ale pod křivkou jednoduché tvary, jejichž obsah známe. Jindy obsah můžeme alespoň přibližně odhadnout.
Obdélníky:
Obsah obdélníka je strana krát strana, zde tedy vlastně s=v\cdot t.
Příklad: Dráha cyklisty
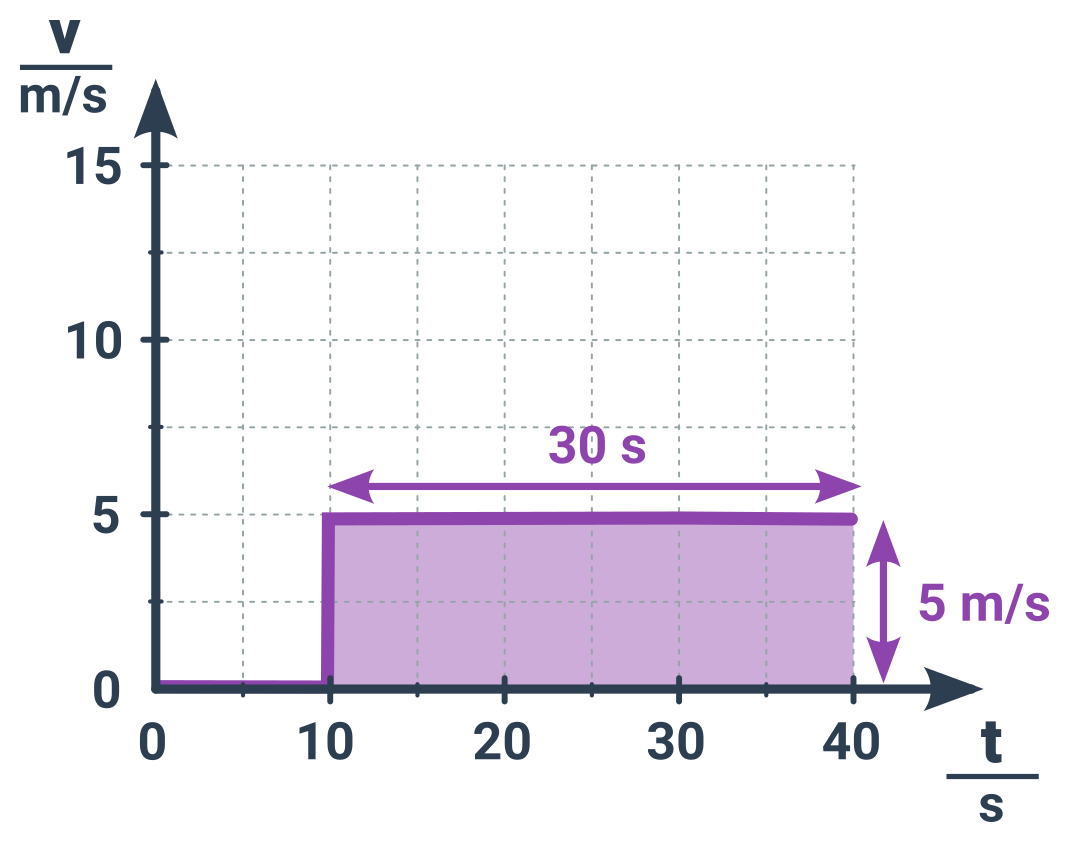
Oblast pod křivkou je obdélník, když jeho rozměry vynásobíme dostaneme ihned výslednou dráhu.

Pozn.: Pravoúhlý trojúhelník má obsah jako polovina obdélníka.
Postup použitelný i pro složitější tvary (minimálně odhad) využívá mřížky grafu. Spočítáme obsah jednoho čtverce mřížky a pak vynásobíme počtem čtverců pod křivkou (nemusí být celé číslo).
Příklad: Dráha cyklisty pomocí mřížky
Z grafu
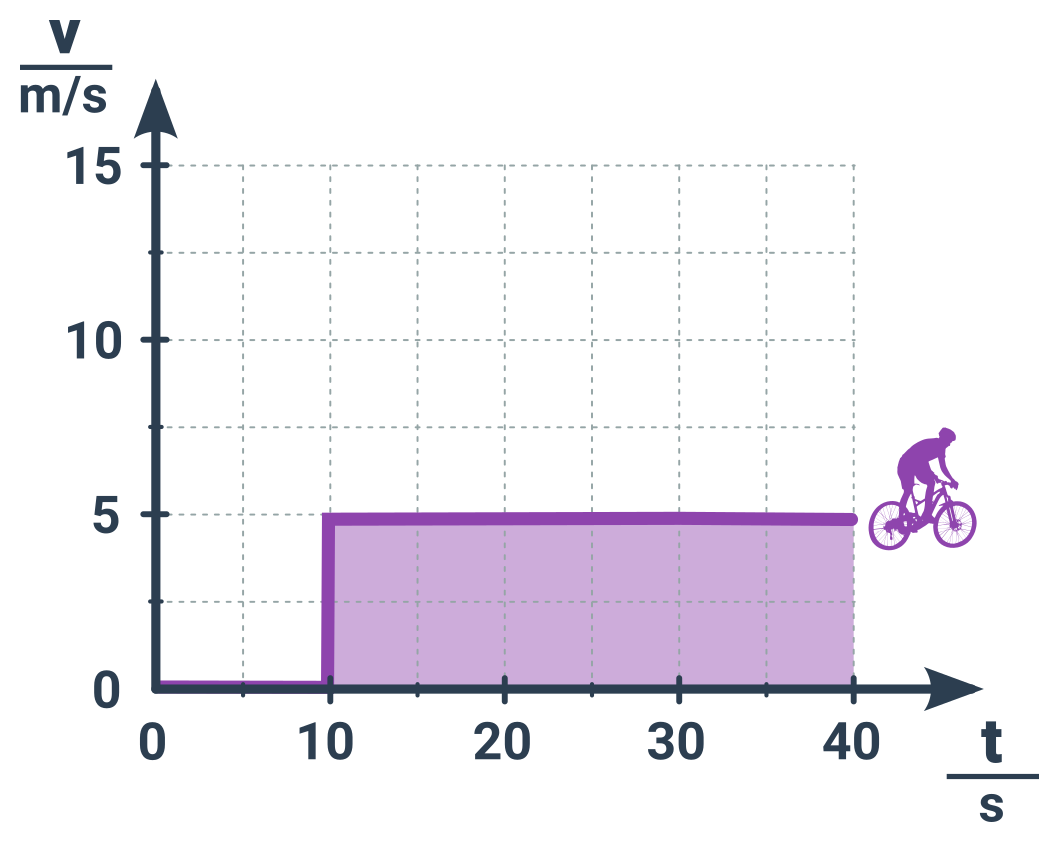
určíme obsah jednoho čtverce mřížky

Pod křivkou je 12 takových čtverců, takže

Vrhy a pády
Vrhy a pády jsou speciálním případem pohybu rovnoměrně zrychleného. Popisují pohyb těles, kterými házíme kolem sebe nebo které padají.
Platí jen tam kde můžeme zanedbat odpor vzduchu (pád hopskulky z okna je ok, ale pád kroupy z mraku nebo listu papíru ze stolu ne) a v omezeném prostoru (ve kterém se téměř nemění zemská přitažlivost, ne pro hod ze země do stratosféry).
- Základem je umět určit o jaký typ vrhu se jedná (volný pád, vrh svislý, vrh vodorovný, vrh šikmý)
- Poté můžeme určit některé vlastnosti takového vrhu.
- Jednotlivým typům se pak můžeme věnovat detailněji, s výpočty a vzorci – aktuálně zde najdeme procvičování volného pádu
Poznávání vrhů
Klasická mechanika popisuje 4 vrhy/pády. Volný pád, vrh svislý, vrh vodorovný a vrh šikmý.
Rozpoznáme je podle trajektorie a rychlosti v:
Trajektorie
- vrh svislý a volný pád → rovná (část přímky)
- vrh vodorovný a vrh šikmý → zakřivená (část paraboly)
U vodorovného vrhu a volného pádu navíc trajektorie začíná nejvyšším bodem.
Rychlost
- volný pád → počáteční úplně nulová, pak svisle směrem dolů
- vrh svislý → počáteční svislý směr, v průběhu svislý směr nebo nulová
- vrh vodorovný → počáteční vodorovný směr, pak vždy šikmo dolů
- vrh šikmý → počáteční šikmý směr, v průběhu i vodorovný (na vrcholu)
V průběhu všech vrhů se vodorovná složka rychlosti (obvykle značená v_\mathrm x) nemění, svislá (v_\mathrm y) ale ano.
Matematicky: vodorovný směr rychlosti znamená v_\mathrm y = 0, svislý směr rychlosti znamená v_\mathrm x=0.
NahoruVlastnosti vrhů
Několik veličin a vlastností, které se pojí s vrhy:
Obecné vlastnosti
- zanedbáváme odpor vzduchu (jinak by byly výpočty mnohem komplikovanější)
- trajektorií je část paraboly nebo úsečka (u vrhu svislého a volného pádu)
- pro popis volíme obvykle dvě souřadnice x (vodorovná) a y (svislá), vrh totiž probíhá v rovině
Veličiny
Rychlost na počátku značíme v_0, v průběhu vrhu pak v. Rychlost dopadu pak v_\mathrm d.
- můžeme je rozložit na vodorovnou a svislou složku (v_\mathrm{0x}, v_\mathrm{0y}, v_\mathrm{x}, v_\mathrm{y}, v_\mathrm{dx} nebo v_\mathrm{dy})
- vodorovná složka se nemění (v_\mathrm{x}=v_\mathrm{0x})
- u vrhu šikmého jsou rychlosti ve stejných výškách stejně velké a svírají stejný úhel s vodorovným směrem (jen v_y se otočí směrem dolů)
Polohu tělesa popisují právě souřadnice x a y
- protože je v_\mathrm{x}=v_\mathrm{0x}, probíhá v souřadnici x rovnoměrný pohyb
- souřadnice y se mění nerovnoměrně – jde vlastně o rovnoměrně zrychlený pohyb se zrychlením g
Čas dopadu se značí obvykle t_\mathrm d a jde o dobu od začátku vrhu do dopadu. Závisí vždy na v_\mathrm{0y} a často na počáteční svislé poloze y_0 (respektive výšce nad zemí h).
NahoruVolný pád
Volný pád znamená, že těleso padá z klidu z počáteční nenulové výšky. Protože je v_0 nula a protože v_\mathrm x se u vrhů nemění, bude v_\mathrm x vždy nulová. Pak není rozdíl mezi svislou rychlostí v_\mathrm y a celkovou rychlostí v, dále tedy mluvíme jen o v.
Pohyb tedy probíhá pouze ve svislém směru a popisuje jej jen souřadnice y. Počáteční svislou polohu y_0 většinou značíme také jako výšku pádu h.
Jde o rovnoměrně zrychlený pohyb se zrychlením g a počáteční rychlostí v_\mathrm {0}=0 (viz výše). V čase t je tedy rychlost rovna g\cdot t a dráha rovna \frac{1}{2}gt^2.
Většinou nás zajímá čas dopadu t_\mathrm d. Můžeme jej vyjádřit z výšky h, protože čase t_\mathrm d musí být dráha rovna právě celé této výšce. Platí tedy rovnice h=\frac{1}{2}gt_\mathrm{d}^2 a úpravou platí i:
t_\mathrm{d}=\sqrt{\frac{2h}{g}}
Nyní můžeme z výšky h vyjádřit i rychlost dopadu v_\mathrm {d}=g\cdot t_\mathrm d. Pokud totiž za t_\mathrm d dosadíme \sqrt{\frac{2h}{g}}, dostaneme v_\mathrm {d}=g\cdot \sqrt{\frac{2h}{g}}, po úpravě:
v_\mathrm {d}=\sqrt{2hg}
NahoruPohyb po kružnici
Z nepřímočarých pohybů je nejdůležitější rovnoměrný pohyb po kružnici. Popisuje situace jako točení na kolotoči, prádlo v bubnu ždímačky nebo otáčení planety Země. Přibližně odpovídá i řadě složitějších situací (např. pohyb v trolejbusu v zatáčce).
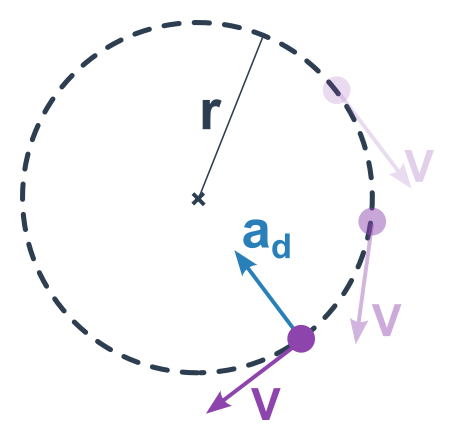
Tedy trajektorií je kružnice. Rychlost v je tečnou k trajektorii (i proto se nazývá obvodová) a má konstantní velikost, mění se ale směr. Zrychlení (které právě popisuje změny směru rychlosti) směřuje do středu kružnice. Říká se mu proto dostředivé a značíme jej a_\mathrm d. Má velikost:
a_\mathrm d=\frac{v^2}{r}
Často nás nezajímá, jak rychle se pohybujeme, ale jak rychle se otáčíme dokola (úhel za jednotku času). Proto definujeme úhlovou rychlost \omega. Pro rovnoměrný pohyb po kružnici je \omega konstantní a úhel otočení \varphi je přímo úměrný času.
Platí vztahy jako \omega=\frac{v}{r} resp. v=\omega\cdot r. Po dosazení za v tak můžeme dostat alternativní vztah pro a_\mathrm d:
a_\mathrm d=\omega^2\cdot r
NahoruDynamika (příčiny pohybu)
Dynamika je část mechaniky, která se snaží vysvětlit, co způsobuje pohyb (přesněji jeho změny).
Základním pojmem je síla, což je působení okolí na těleso. Má velikost (jak moc působí) a směr (kterým směrem mě například táhne). Síly působící na stejné těleso často sčítáme (neboli skládáme) do jedné výsledné síly. Souvislost výsledných sil s pohybem popisují Newtonovy pohybové zákony.
Síla může mít různý původ (mechanický tah provazu, neviditelná přitažlivá síla magnetu, …), rozeznáváme tedy různé typy sil. Některé konkrétní typy sil, kterými se zabýváme samostatně:
- Ve vesmíru počítáme s gravitačními silami.
- Na Zemi je gravitace doplněna odstředivou silou otáčení země na tíhovou sílu. Definujeme taky tzv. tíhu.
- Stlačování těles (například opěrky sedadla našimi zády) popisuje tlaková síla a s ní související veličina tlak.
- Pokud po sobě dva povrchy klouzají dochází k smykovému tření, které můžeme popsat třecí silou.
Pokud se nezajímáme jen o posuvný pohyb těles, mohou mít síly i otáčivé účinky. To popisuje veličina moment síly, pomocí které můžeme otáčení těles i vypočítat.
Kromě sil definujeme v dynamice taky veličinu zvanou hybnost, která se hodí zejména pro popis soustavy více těles.
NahoruSkládání sil
Skládání, neboli sčítání sil je nejčastěji potřeba, když zjišťujeme výslednou sílu působící na těleso. Protože síla je vektorová veličina, skládání sil je vlastně sčítáním vektorů. Proto následující odstavce platí i pro jakoukoliv jinou vektorovou veličinu (např. hybnost, moment síly, …).
U sčítání více sil (F_1, F_2, F_3, …) často výslednou sílu označujeme bez indexu (F), v příkladech níže ji ale pro jednoznačnost označíme indexem „celk“.
Síly ležící v jedné přímce
Nejjednodušší je, když leží všechny síly v jedné přímce (např. všechny míří vodorovně doprava nebo doleva):
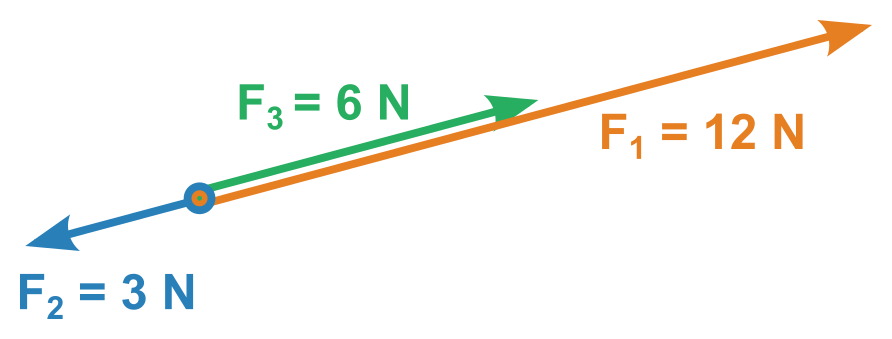
- Zvolíme směr (jeden z těch dvou).
- Přičítáme velikosti sil mířících zvoleným směrem, a odečítáme ty opačné.
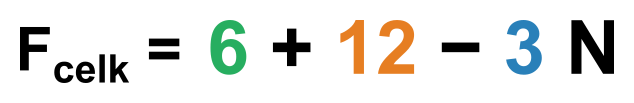
- Vyjde nám velikost (délka) výslednice. Pokud je kladná, míří námi zvoleným směrem, pokud ne, míří na druhou stranu.
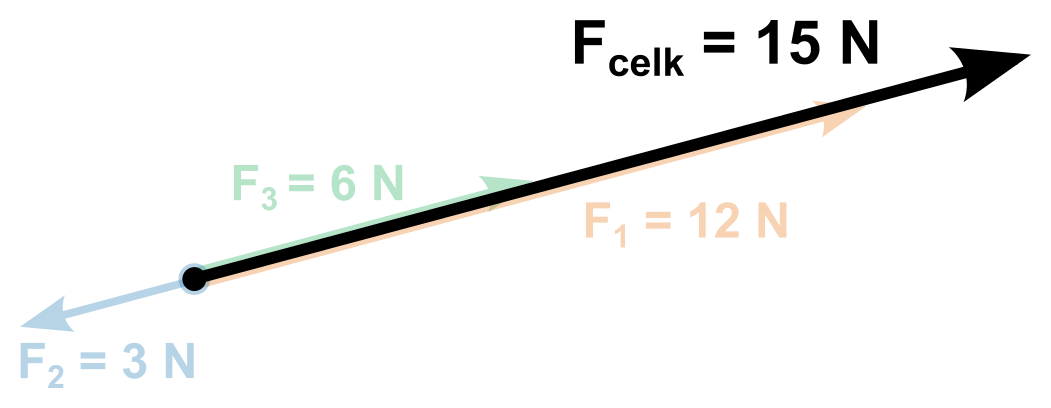
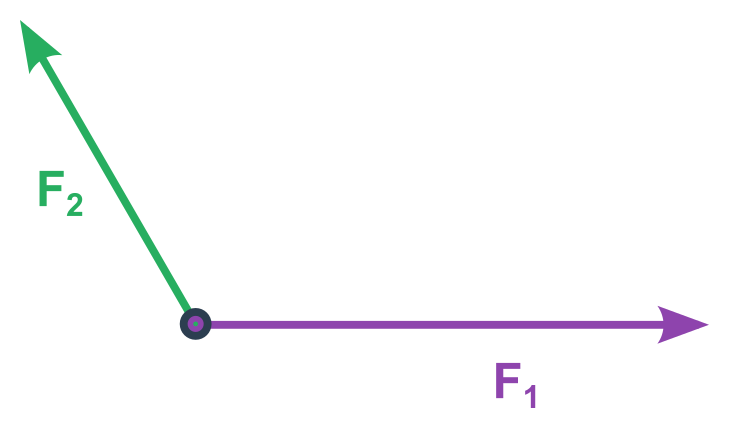
Dvě síly neležící v jedné přímce (grafické řešení)
- Síly narýsujeme tak, aby vycházely z jednoho bodu/působiště
- Doplníme na rovnoběžník. Výsledkem je jeho úhlopříčka vycházející ze společného počátku sil
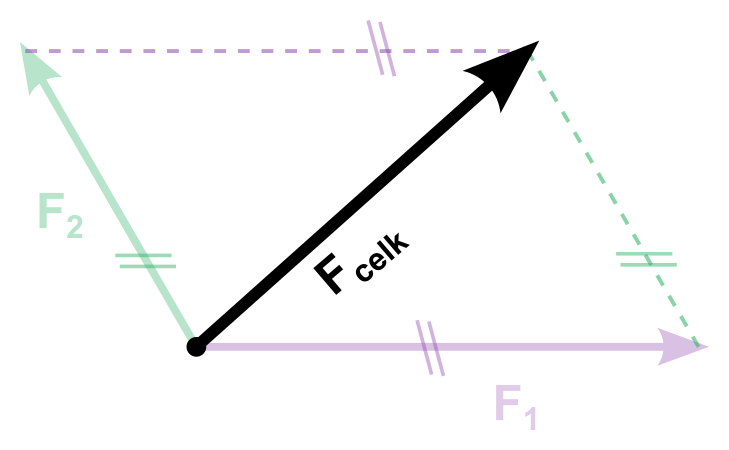
Pokud jsou na sebe síly kolmé, jde o úhlopříčku obdélníka s délkou podle Pythagorovy věty F=\sqrt{F_1^2+F_2^2}.
Více sil neležících v jedné přímce (grafické řešení)
- Vektory narýsujeme tak, aby vycházely z jednoho bodu/působiště
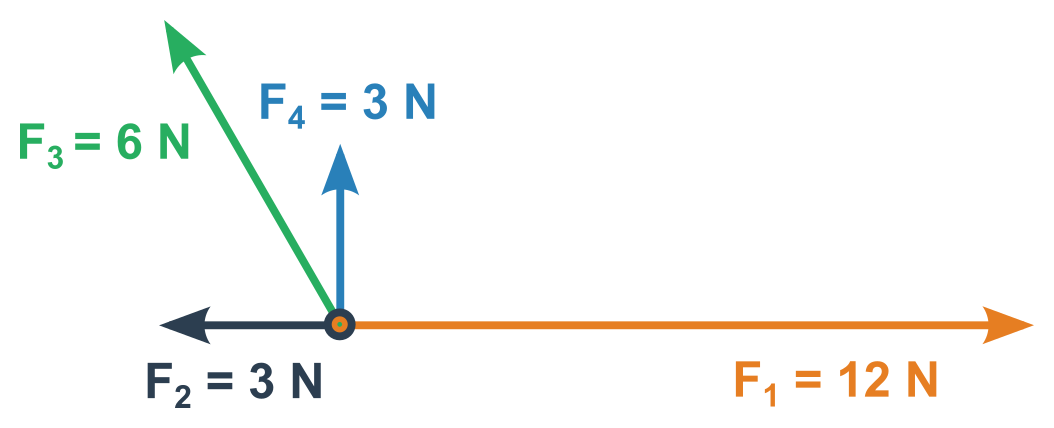
- Doplňováním na rovnoběžník sčítáme postupně jednotlivé vektory dokud nezbyde jeden výsledný vektor (pořadí je na nás, nejjednodušší je ale sdružovat rovnoběžné síly a následně ty na sebe kolmé)
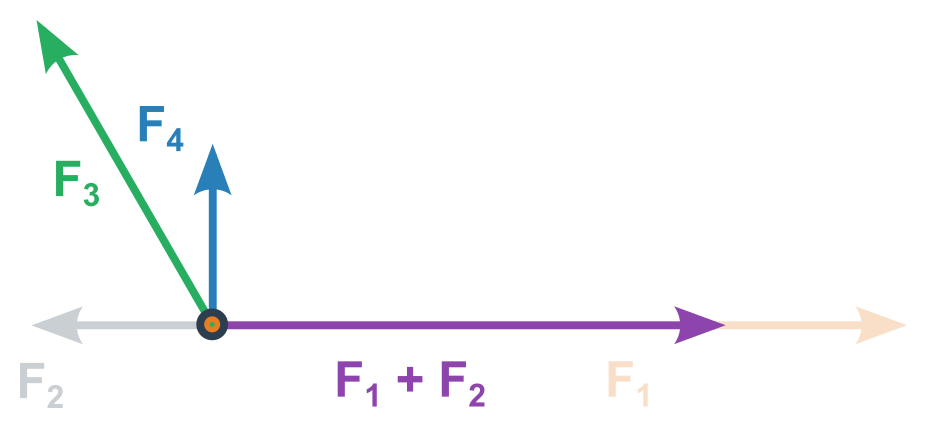
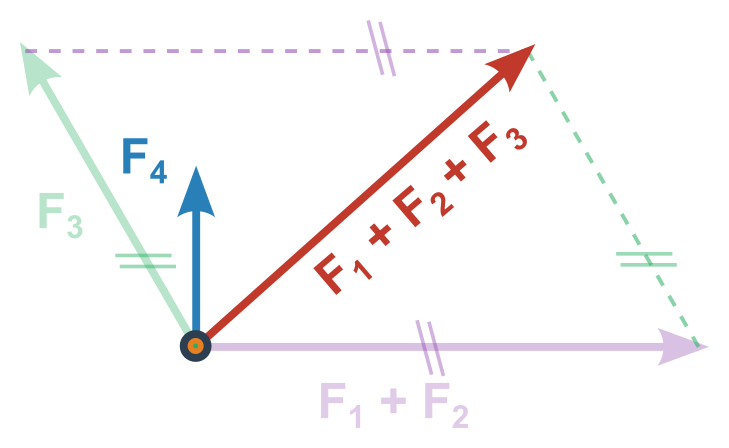
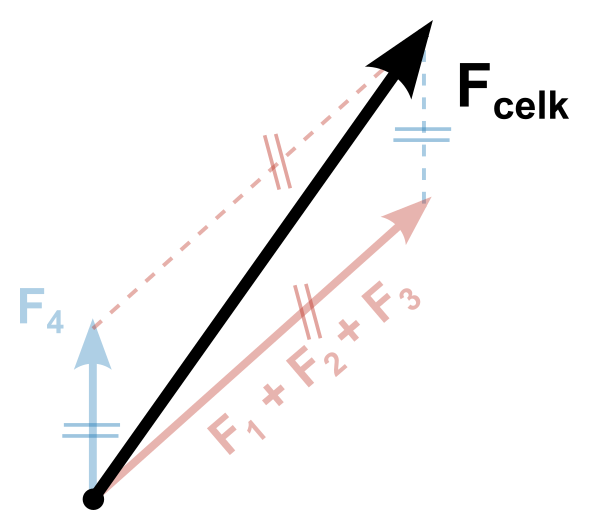
Souřadnicové řešení
- Musíme zvolit nějakou kartézskou soustavu souřadnic, například ve směru jedné ze sčítaných sil.
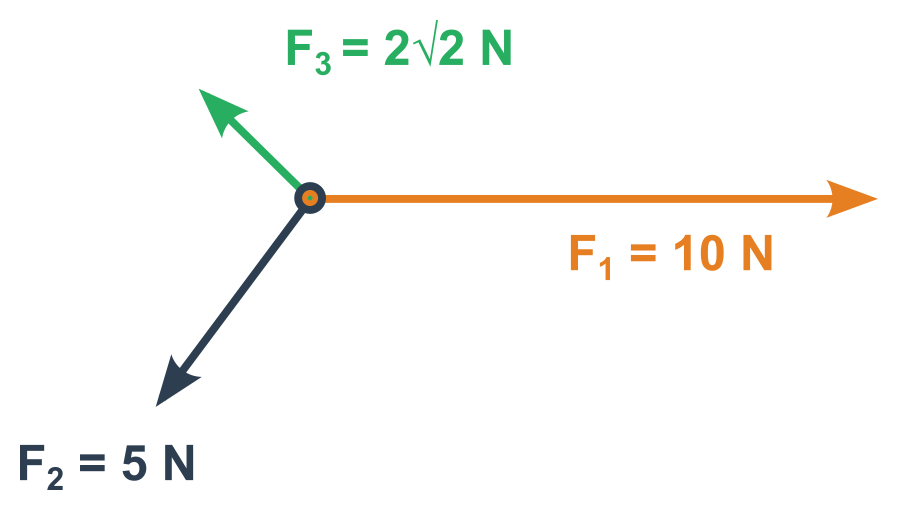
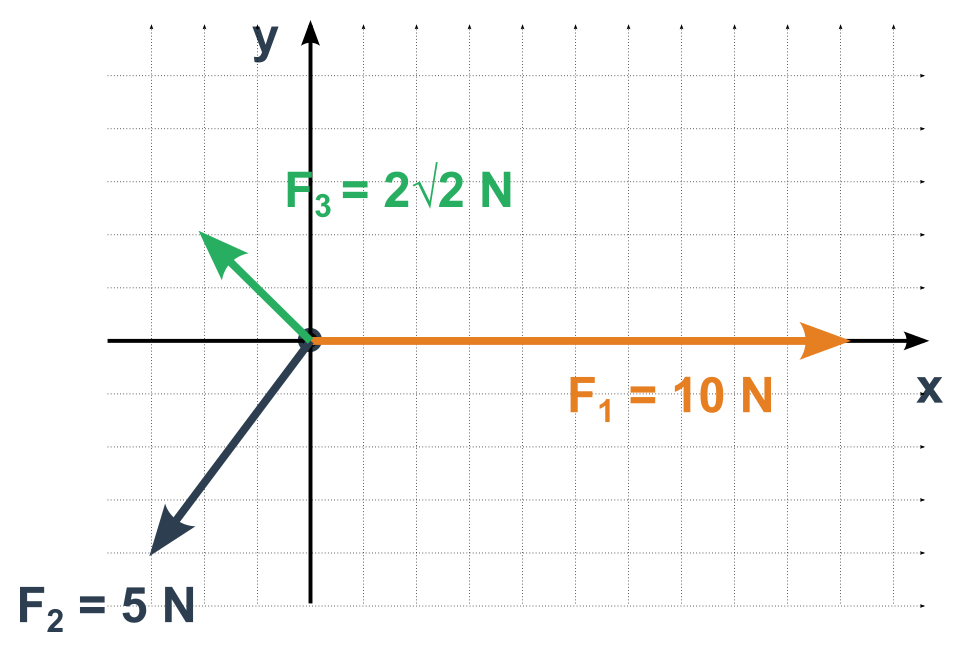
- Určíme jednotlivé složky všech vektorů sil v této soustavě
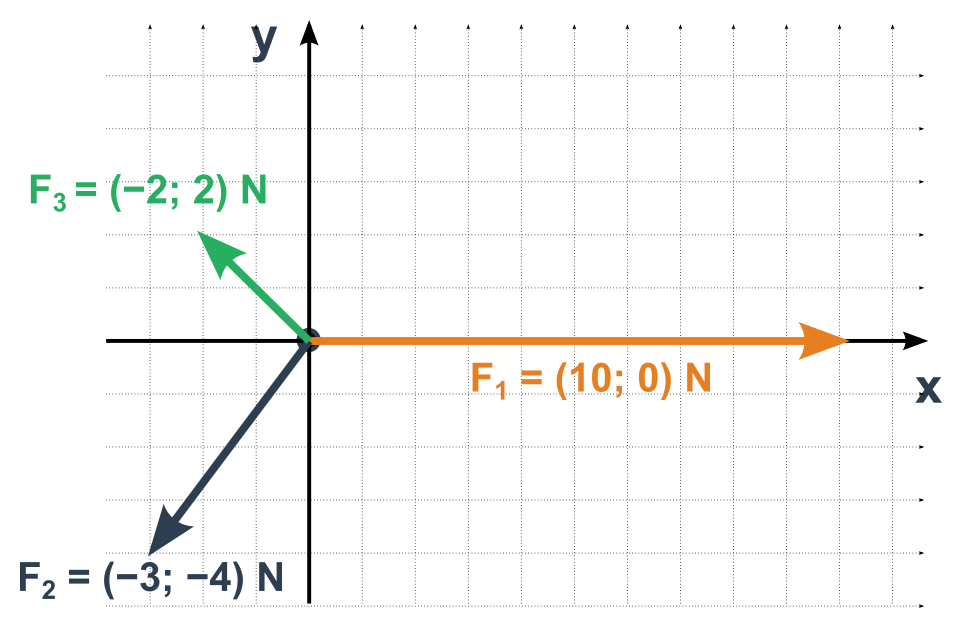
- Sečteme zvlášť stejné složky všech sil

- Výsledkem je vektor výsledné síly o souřadnicích které nám vyšly
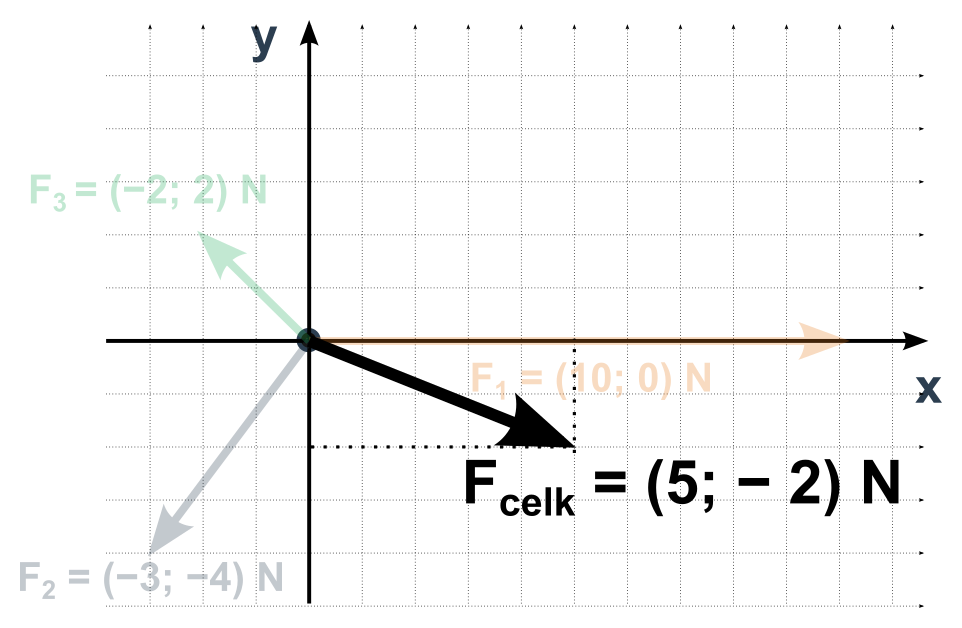
Velikost je podle Pythagorovy věty odmocnina z druhých mocnin souřadnic (zde odmocnina z 5^2+(−2)^2, tedy \sqrt{29}).
Tipy
Pokud jsou na sebe dvě síly kolmé, určíme délku výsledné síly i se znalostí úhlopříček obdélníka (Pythagorova věta, F_\mathrm{celk}=\sqrt{F_1^2+F_2^2})
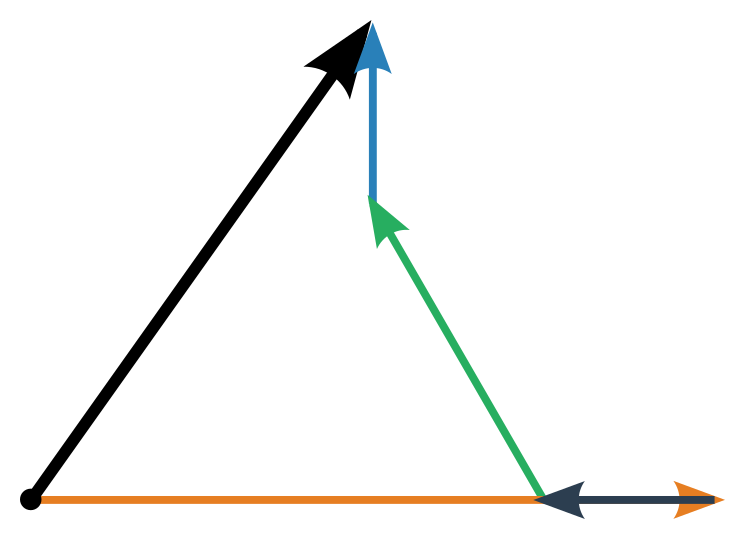
Alternativně můžeme grafické skládání sil pojmout tak, že síly připojujeme jednu za druhou jako na řetěz (viz obrázek). Je to sice názornější, ale rýsovalo by se to mnohem hůř.

Newtonovy pohybové zákony
Newtonovy zákony jsou pravidla, která popisují vztah pohyb tělesa – síly na těleso působící. Jsou tři:
- První Newtonův zákon: Zákon setrvačnosti – vysvětlí, proč se musíme v autobuse držet, když stojíme.
- Druhý Newtonův zákon: Zákon síly – ukazuje přímou úměru mezi součtem sil působících na těleso a jeho zrychlováním.
- Třetí Newtonův zákon: Zákon akce a reakce – aneb, když nás táhne gravitace k zemi, my táhneme zeměkouli stejnou silou nahoru.
Zákon setrvačnosti
Také známý jako první Newtonův zákon. Jeho původní znění je v latině, překlad je přibližně následující:
Těleso setrvává v klidu nebo rovnoměrném pohybu v daném směru, není-li nuceno vnějšími silami tento stav změnit.
„V daném směru“ znamená především rovnoměrný přímočarý pohyb (konstantní vektor rychlosti \vec v). Může mít ale i další význam (viz Zajímavosti).
Těleso není „…nuceno vnějšími silami tento stav změnit…“ právě tehdy, když je výslednice (vektorový součet všech sil působících na těleso), nulová.
\vec F_1+\vec F_2+\vec F_3+\dots=\vec 0 \;\;\;\implies\;\;\; \vec v=\mathrm{konst.}
Tento zákon platí jen v inerciálních soustavách.
Důsledky
- Pokud je výslednice sil nulová, vektor rychlosti \vec v se nemění. Ani jeho velikost, ani jeho směr.
- Pohyb za nepřítomnosti sil sám nezastaví.
- I za přítomnosti sil může být pohyb/klid tělesa neměnný (pokud je jejich výslednice nulová).
Zajímavosti
Původní znění je „Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus illud a viribus impressis cogitur statum suum mutare.“
Výzkum původních Newtonových děl ukazuje , že první zákon zahrnuje i setrvačnost otáčivého pohybu a tedy není jen speciálním případem druhého Newtonova zákona¹. Příklady spojenými s rotací se nicméně cvičení nezabývají.
Zákon síly: se vztahy
Také je znám jako druhý Newtonův zákon, je jedním z nejdůležitějších zákonů, které popisují dynamiku pohybu (proč objekty mění svůj pohyb).
Matematicky je vyjádřen jako rovnice mezi výslednicí sil působících na těleso (\vec F), jeho zrychlením (\vec a) a setrvačností tělesa vyjádřenou jeho hmotností (m).
\vec F=m\cdot \vec a
Rovnice napsaná bez znázornění vektorových veličin (F=m\cdot a) je také častá, zejména když není směr zrychlení důležitý (např. vše probíhá na přímce).
- Těleso o hmotnosti 1 kg se pohybuje se zrychlením 1 m/s² → síla 1 N.
- Láhev limonády (2 kg) padá se zrychlením asi 10 m/s² → síla 20 N.
- Karta BANGu (0,001 g) klouže po stole a brzdí se zrychlením 2 m/s² → síla 0,002 N.
Jiné tvary
Pomocí matematických úprav můžeme dojít k dalším tvarům:
\vec a=\frac{\vec F}{m}
Tento tvar je fyzikálně asi nejlogičtější, protože zrychlení, které je z našeho pohledu následek (levá strana rovnice), je důsledkem příčin tohoto pohybu (přítomnost sil \vec F, setrvačnost tělesa kvůli hmotnosti m).
- Sáně s dítětem (10 kg) táhne výsledná síla 5 N → Síla způsobí zrychlení saní 0,5 m/s².
- Auto (1500 kg) brzdí s výslednou silou 6000 N → Zrychlení (resp. zpomalení) auta bude 4 m/s².
m=\frac{F}{a}
Protože je hmotnost skalár, je podílem velikostí obou vektorů, což můžeme zapsat právě jako \frac{F}{a} (bez šipek) nebo uzavřením vektorů do svislých čar m=\frac{\lvert\vec F\rvert}{\lvert\vec a\rvert}.
- Vláček pohání výsledná síla o velikosti 0,3 N a pohybuje se se zrychlením 1,5 m/s². → Musí mít hmotnost 0,2 kg.
Zajímavosti
Protože \vec F i \vec a jsou vektory a m je jen skalár (číslo) směřují zrychlení i výsledná síla stejným směrem.
Zákon síly není definicí síly, protože o ní nic konkrétního neříká (odkud se vzala, jaká je, …).
Původní Newtonova formulace
Mutationem motus proportionalem esse vi motrici impressae et fieri secundam lineam rectam qua vis illa imprimitur.
Zákon akce a reakce
Zákon akce a reakce, neboli třetí Newtonův zákon popisuje vzájemné působení (interakci) dvou těles.
Definice
Každé působení prvního tělesa na druhé (silou \vec F_{12}), neboli akce, vyvolává stejně velkou, opačně orientovanou reakci působení druhého tělesa na první (\vec F_{21}).
Matematicky to můžeme vyjádřit jako \vec F_{12}=-\vec F_{21}.
Taková dvojice sil vypadá následovně:
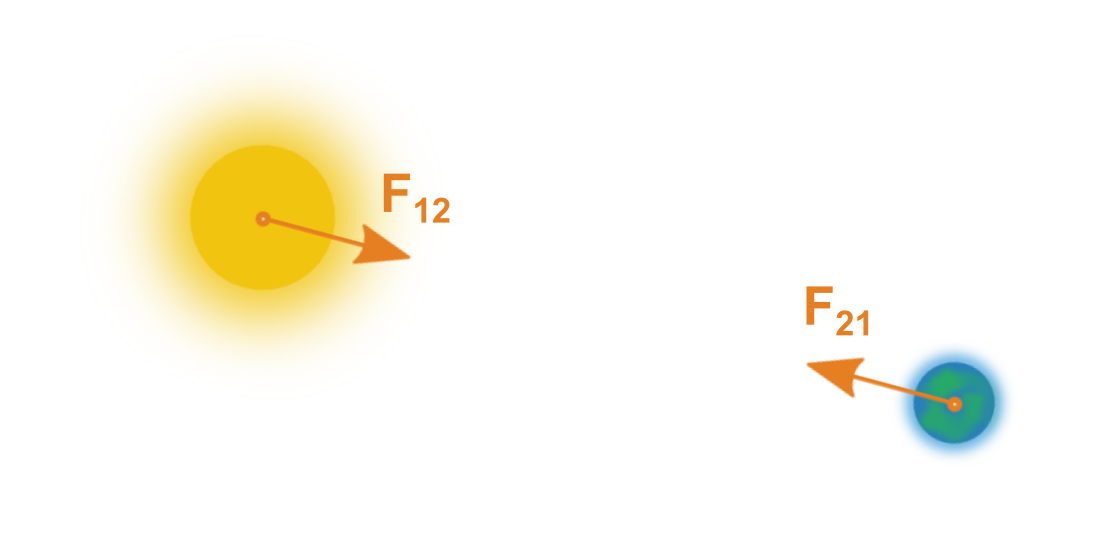
- Země přitahuje Slunce stejně velkou silou jako Slunce přitahuje Zemi (jen je ta síla na obrovskou hmotnost Slunce relativně slabá).
- Tlačíme nepojízdné auto silou F. Auto zase otlačuje naše ruce silou -F
- Raketoplán urychluje hořící palivo z trysek dozadu. Toto palivo jej tedy tlačí kupředu.
- Když chceme udělat krok, třením podrážky odstrkujeme zeměkouli dozadu. Na oplátku na nás země pusobí silou směrem vpřed, která naše tělo rozpohybuje.
- Když narazí kulečníková koule do druhé, zapůsobí na ni silou a rozpohybuje ji. Ale sama přitom svůj pohyb změní. Ta druhá koule tedy musela zapůsobit zase na ni.
Vlastnosti
Ačkoliv jsou síly opačně orientované a stejně velké, jejich výslednice není nulová. Působí totiž každá na jiné těleso, nemůžeme je tedy sčítat.
Akce i reakce na ni probíhají okamžitě (alespoň v Newtonovském pojetí času), společně vznikají a společně zanikají. Nelze tedy určit, která je první.
- Když se opřeme
Zajímavosti
- „Actioni contrariam semper et aequalem esse reactionem; sive: corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.“ (Newtonova formulace)
- Protože jsou akce i reakce současné a nerozlišitelné, dalo by se o tomto zákonu s trochou drzosti mluvit spíše jako o zákonu INTERakce.
- Důsledkem zákona akce a reakce je i zákon zachování hybnosti.
Síly, které pozorujeme kolem nás, mají různý původ a hodí se umět je rozlišovat.
V mechanice se setkáme s kontaktními silami, které se objeví jen při kontaktu dvou těles/látek. Dělíme je na normálové (kolmo k povrchu v místě kontaktu) a tečné (podél). Mezi normálové patří zejména síly tahu a tlaku (víceméně všechny spoje a kontaktní plochy těles). Tečné jsou pak různé síly odporu prostředí během pohybu (třecí síla, odpor větru, …), bez kterých bychom naše auta nemohli ani rozjet, ani zastavit.
Na dálku (bezdotykově) pak působí gravitační síla mířící do těžiště druhého tělesa (např. do středu Země). Mimo klasickou mechaniku se setkáme s dalšími dalekodosahovými bezdotykovými silami – elektrickou mezi elektrickými náboji (např. elektrostatickou na nabitých baloncích) nebo magnetickou mezi magnety (objevuje se ale i tam, kde proudí elektrický proud).
Speciální název mají i některé součty sil. Například pod vodou je na těleso zespodu větší tlaková síla než shora. Součet tlakových sil na toto těleso, jej tedy nadlehčuje – vztlaková síla. Zemská přitažlivost je u nás zase zmenšována odstředivou silou rotace Země. Součet, který vnímáme, tedy nazýváme tíhovou silou.
Zajímavosti
Ve skutečnosti jsou úplně všechny z výše zmíněných sil kromě gravitačních elektromagnetického původu. Na mikroskopické úrovni je totiž zprostředkují atomy. Například když proti sobě tlačíme dva materiály, je tlaková síla jen projevem elektrostatického odpuzování krajních atomů.Newtonův gravitační zákon
Gravitační působení mezi dvěma tělesy popisuje podle Newtona gravitační síla F_g:
F_g=G\frac{m_1\cdot m_2}{r^2}
kde G je gravitační konstanta (často se také značí \kappa), m_1 a m_2 jsou hmotnosti těles a r je vzdálenost jejich středů hmotnosti (těžišť). Používáme ji většinou ve vesmíru, kde jsou vzdálenosti mnohem větší než rozměry těles, takže často neuděláme velkou chybu když za r bereme vzdálenost mezi předměty.
Gravitační síly jsou vždy přitažlivé a jde o síly akce a reakce (vždy vznikají dvě, obě stejně velké opačně orientované).
Definujeme i gravitační zrychlení a_g. Na rozdíl od gravitační síly není závislé na obou hmotnostech – např. zrychlení způsobené tělesem 2 je podle druhého Newtonova zákona a_g=F_g/m_1.
Tedy po dosazení do F_g je a_g=\kappa\frac{m_2}{r^2}.
Protože stejně velké gravitační síly těles 1 a 2 dělíme různými hmotnostmi, nejsou gravitační zrychlení stejně velká.
Gravitační konstanta \kappa má hodnotu 6,67⋅10⁻¹¹ m³s⁻²kg⁻¹.
Příklad: člověk a Země
- Máme zjistit podle F_g=\kappa\frac{m_1\cdot m_2}{r^2} sílu mezi člověkem stojícím na zemi a jeho planetou.
- m_1 je asi 100 kg, tedy 10² kg
- m_2 je asi 6⋅10²⁴ kg
- r je přibližně poloměr Země 6378 km, zaokrouhleně 6,3 milionů metrů, tedy 6,3⋅10⁶ m
- Zde bychom tedy r jako vzdálenost těles (0 m) brát nemohli.
- Dosadíme spolu s konstantou \kappa do vzorce:
- F_g=6,67⋅10⁻¹¹ \frac{10²\cdot 6⋅10²⁴}{6{,}3⋅10⁶⋅6{,}3⋅10⁶}\,\mathrm{N}=\frac{6,67⋅6}{6{,}3⋅6{,}3}10³\,\mathrm{N}\approx10³\,\mathrm{N}
- Na 100kg člověka tedy působí asi 1000 N gravitační síla.
- To sedí i na jednodušší tíhovou sílu F_G=m_1\cdot g (u země je g\approx 10\,\mathrm{m⋅s⁻²})
Gravitační vs. tíhová síla a tíha
Tíhová síla
Pro popis dynamiky pohybu na zemi a u země nepoužíváme přímo gravitační sílu F_g, protože to úplně nevychází. Nacházíme se totiž na rotující (Země)kouli a v naší vztažné soustavě musíme započítat odstředivou sílu.
Tento součet (gravitační a odstředivé síly) označujeme jako tíhovou sílu F_G. Podobně máme místo gravitačního zrychlení a_g tíhové zrychlení g. Působištěm tíhové síly je těžiště tělesa (stejně jako u gravitační síly).
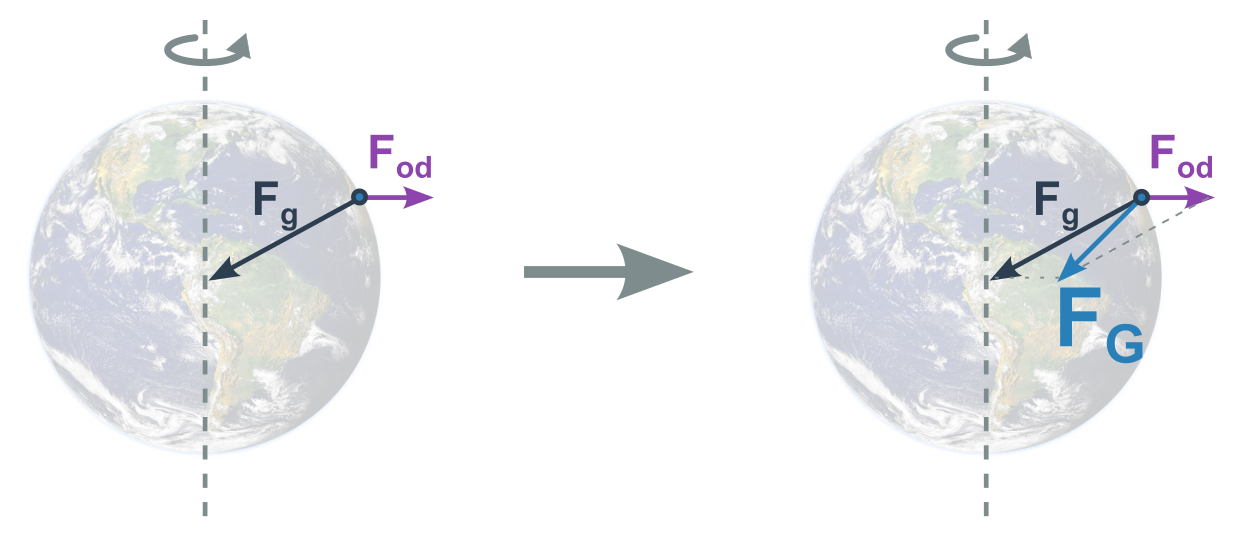
Tíha
Ani tíhová síla není ale vždy rovna velikosti síly, jakou tlačí např. naše nohy na podlahu pod námi.
Proto zavádíme tíhu G. Jde v podstatě o tlakovou sílu na podložku (způsobenou tíhovou silou). Působištěm tíhy je místo kontaktu s podložkou. Rozdíl ve velikosti mezi tíhou a tíhovou silou poznáme u soustav zrychlujících ve svislém směru.
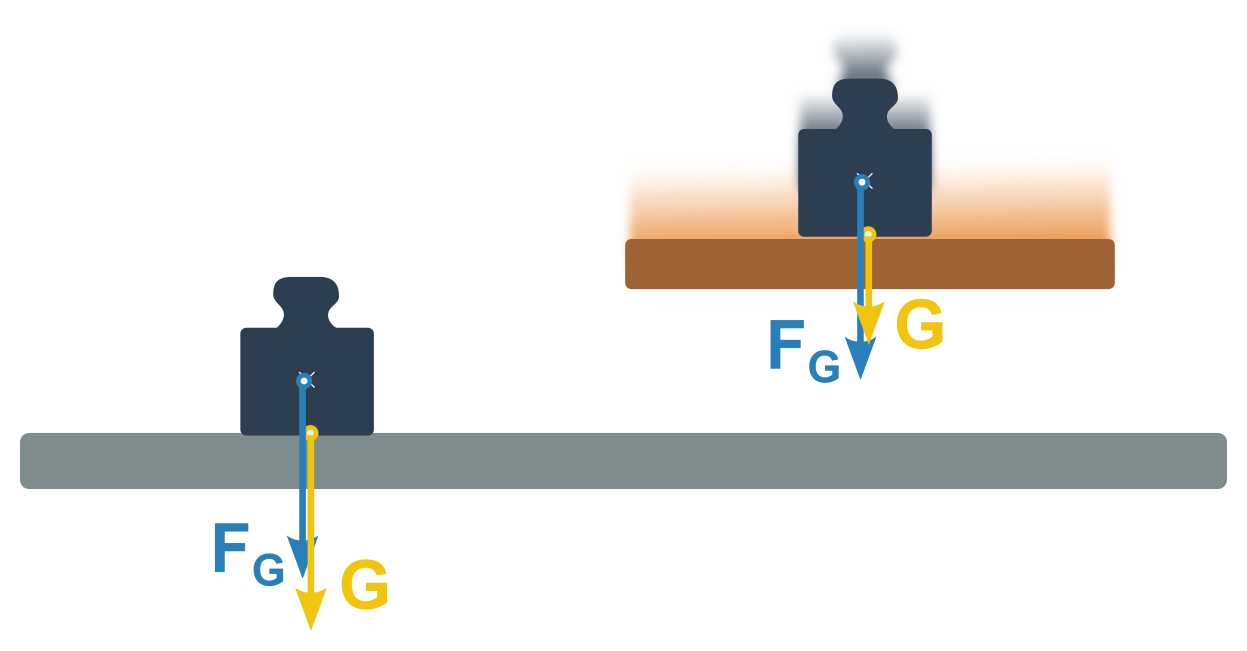
Příklad : Výtah
- Ve výtahu na nás působí stále stejná tíhová síla F_G.
- Když se ale výtah rozjíždí nahoru, cítíme se těžší – je totiž větší naše tíha G.
- Při rozjezdu směrem dolů je naše tíha naopak menší.
- kdyby výtah začal padat volným pádem, bude naše tíha dokonce nulová. Ale to nechceme…
Tlak a tlaková síla
Definice
Tlak (značíme p) je veličina popisující deformační (ne pohybové) účinky síly na těleso. Je definován pomocí tlakové síly \vec F působící kolmo na určitou plochu S.
p = \frac{F}{S}
Úpravou rovnic (nebo pomocí vztahového trojúhelníku níže) můžeme odvodit další vztahy:
F = p \cdot S
S = \frac{F}{p}
Jednotky
Jednotkou je (jak ze vztahu p = F/S vyplývá) newton na metr čtvereční (N/m²). Tato jednotka dostala také vlastní název – pascal.
Typicky se setkáváme se silami v jednotkách až stovkách newtonů působícími na plochy mnohem menší než je metr čtvereční. Proto se kolem nás setkáváme nejčastěji s tlaky v tisících, ne-li milionech pascalů.
Vtip o jednotkách
Archimedes, Pascal a Newton hrají na schovávanou. Archimedes piká. Pascal se rychle schová do křoví.
Newton se vůbec neschovává, jen do hlíny klackem namaluje čtverec metr krát metr a postaví se do něj.
Archimedes dopiká, okamžitě uvidí Newtona a volá: „Deset dvacet Newton!“
Newton v klidu řekne: „Nene. Newton na metr čtvereční je přece pascal!“
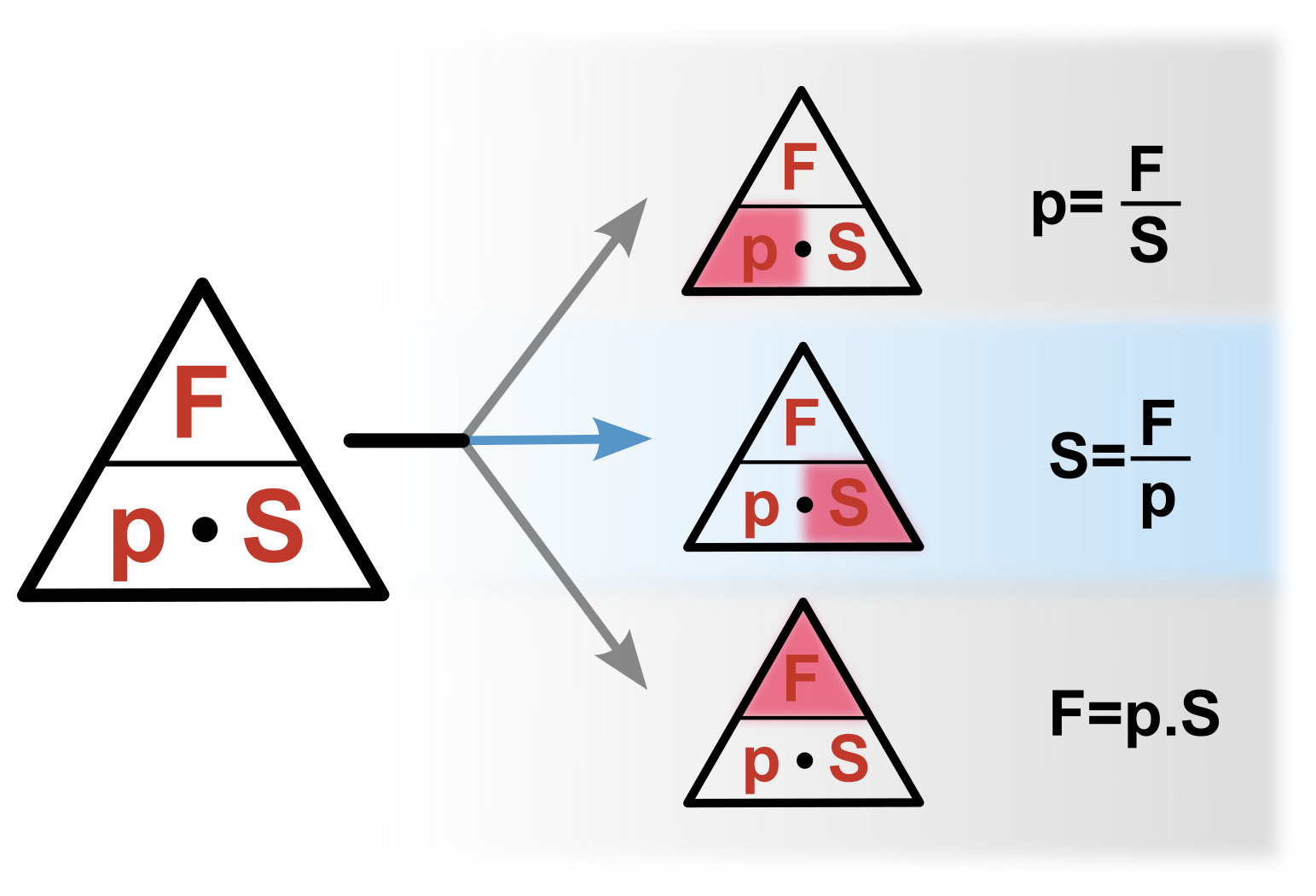
Vztahový trojúhelník
Pro získání vzorce pro libovolnou veličinu p, F, S můžeme použít vztahový trojúhelník (pyramidu). Více o tom jak se vytváří a funguje najdete zde.
Zajímavost: Jednotka SI
Jednotka pascal je v soustavě SI teprve od roku 1971.
Poznámka: Ne vždy lze jednoduše znázornit tlakovou sílu s působištěm v místě doteku (např. více končetin). Proto v některých příkladech používáme k ilustraci i tíhovou sílu s působištěm v těžišti. Má totiž stejnou velikost jako tlaková síla, kterou vyvolává.
NahoruSmykové tření: základy
Mezi dvěma tělesy, která jsou v kontaktu, působí různé síly. Jednou skupinou těchto sil je působení mezi jejich povrchy, pokud jsou v přímém kontaktu (doteku).
Když se dvě tělesa po sobě sunou dochází ke smykovému tření (sunutí=smýkání). Vzniká tzv. třecí síla namířená proti směru pohybu (nebo proti směru, ve kterém se o pohyb snažíme). Záleží na tlakové síle a vlastnostech povrchů obou materiálů (hlavně nerovnosti a jak do sebe zapadají).
Jak po sobě umí daná dvojice materiálů klouzat vyjadřuje experimentální konstanta, tzv. koeficient smykového tření (čím nižší, tím lepší klouzání).
| Materiály | Koeficient |
|---|---|
| ocelový nůž brusle a led | 0,03 |
| hladká ocel a mosaz (naolejované) | 0,11 |
| cihla a suché dřevo | 0,60 |
| pneumatika a suchý asfalt | 0,72 |
| guma a guma | 1,16 |
| (většinou se f pohybuje v rozmezí 0 až 1) |
Smykové tření dělíme na klidové (statické) a smykové tření v pohybu (dynamické).
Klidové tření
Probíhá, dokud jsou tělesa vzájemně v klidu a ještě nedochází ke smýkání (i když se jej nějaká síla snaží vyvolat). Třecí síla je tím, co rozpohybování brání. Například jde o:
- auto zabrzděné v kopci
- sešit ležící na křivém stole
- skříň, kterou se snažíme posunout, ale nemůžeme s ní ani hnout
Třecí síla je pak rovna silám, které se pokoušejí vyvolat vzájemný pohyb. Má ale svoji horní hranici. Pokud je překročena, tělesa se začnou smýkat a přesouváme se do kategorie smykového tření v pohybu.
Smykové tření v pohybu
Setkáme se s ním, když se po sobě tělesa pohybují. Funguje jako brzda působící proti směru pohybu. Jde například o:
- dítě klouzající po skluzavce
- tužku píšící na papír
- koleno drásající se o asfalt
- nebo i ten sešit, když se jej pokusíme položit na příliš nakloněný povrch
Smykové tření: se vzorci a třecí silou
Mezi dvěma tělesy, která jsou v kontaktu, působí různé síly. Jednou skupinou těchto sil je působení mezi jejich povrchy, pokud jsou v přímém kontaktu (doteku).
Tyto síly jsou mikroskopické (slabé vazby mezi nejbližšími atomy) i makroskopické (nerovnosti které do sebe zapadají) a mají většinou hlavní vliv na pohyb jednoho tělesa po druhém. Pokud se tělesa po sobě sunou (nevalí), říkáme účinkům takových sil smykové tření (sunutí=smýkání).
Sílu, která směřuje proti směru pohybu (nebo proti směru, ve kterém se o pohyb snažíme), nazýváme třecí silou F_t. Tato třecí síla záleží na tlakové síle F_N, kterou proti sobě povrchy působí, a na tom, jak dobře po sobě povrchy umí klouzat. To pro danou dvojici materiálů vyjadřuje experimentální konstanta koeficientu smykového tření f.
| Materiály | Koeficient f |
|---|---|
| ocelový nůž brusle a led | 0,03 |
| hladká ocel a mosaz (naolejované) | 0,11 |
| cihla a suché dřevo | 0,60 |
| pneumatika a suchý asfalt | 0,72 |
| guma a guma | 1,16 |
| (většinou se f pohybuje v rozmezí 0 až 1) |
Smykové tření dělíme na klidové (statické) a smykové tření v pohybu (dynamické).
Klidové tření
Probíhá, dokud ještě nedochází ke smýkání, i když se jej nějaká síla snaží vyvolat. Například jde o:
- auto zabrzděné v kopci
- sešit ležící na křivém stole
- skříň, kterou se snažíme posunout, ale nemůžeme s ní ani hnout
Třecí síla je pak stejně velká jako výslednice sil, které se pokoušejí vyvolat pohyb. Maximální klidová třecí síla je vyjádřena z F_N a f jako
F_t=f\cdot F_N
pokud tuto hodnotu ostatní síly překonají, těleso se rozpohybuje.
Smykové tření v pohybu
Funguje jako brzda působící proti směru pohybu. Jde například o:
- dítě klouzající po skluzavce
- tužku píšící na papír
- koleno drásající se o asfalt
- nebo i ten sešit, když se jej pokusíme položit na příliš nakloněný povrch
Tření v pohybu je o něco slabší, než maximální klidové tření. Výpočet F_t=f\cdot F_N platí i zde, ale koeficient f je v pohybu nižší. Např. pneumatika ve smyku nebude mít f=0{,}72 ale jen f=0{,}65. Často se tedy i označují odlišně – například f_0 v klidu a f v pohybu.
Zajímavosti
- Nižší f v pohybu můžeme vysvětlit tak, že povrchy nemají dost času do sebe co nejlépe zapadnout.
- Protože je pohybové tření menší než to klidové, znamená to, že kvádr, který jednou po nakloněné rovině rozjede, se už nezastaví. Až dole.
Hybnost je vektorová fyzikální veličina, kterou značíme \vec p (její velikost je p) a která je definovaná poměrně jednoduše – jako součin rychlosti tělesa a jeho hmotnosti. Jednotkou je tedy součin jednotek obou veličin – kg⋅m/s.

Matematicky hybnost zapisujeme takto:
\vec p=m\cdot \vec v.
Protože jde o vektorovou veličinu, musíme za změnu hybnosti považovat nejen její zmenšení/zvětšení, ale i změnu jejího směru (tedy směru rychlosti).
Na první pohled je zavedení takové veličiny zbytečné (pouze násobek rychlosti). Je ale důležitá pro popis soustavy více těles. Můžeme určit celkovou hybnost soustavy – součet hybností jednotlivých těles (vektorový součet, viz obrázek).
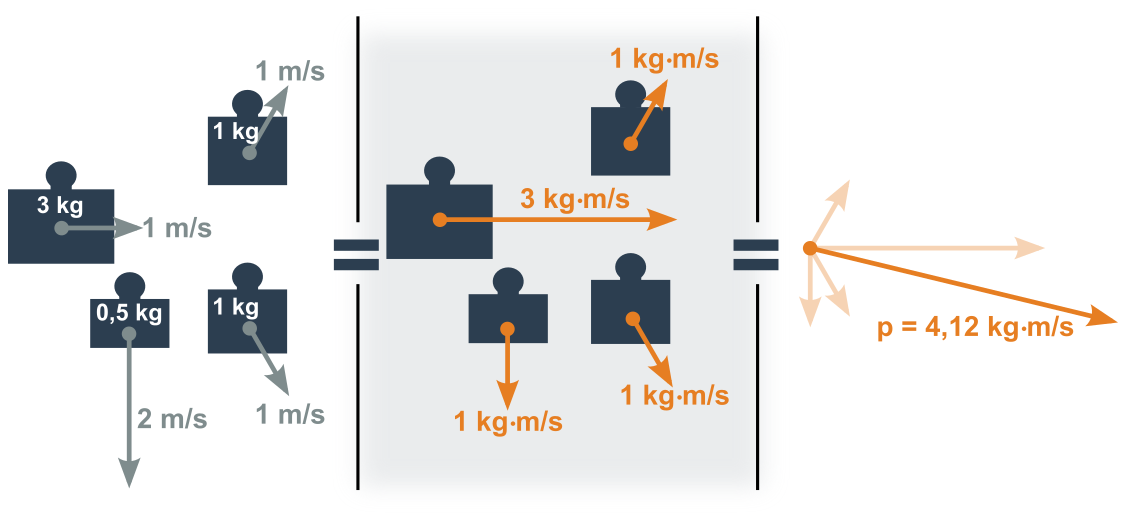
Matematicky zapsáno:
\vec p = \vec p_1+\vec p_2+\vec p_3+\cdots
Celková hybnost těles izolované soustavy se nemění, ať se mezi nimi děje cokoliv (srážky, tření, gravitační přitahování, magnetické síly, …). Říká se tomu zákon zachování hybnosti.
Zajímavosti
- Na principu zákona zachování hybnosti jsou založeny sporty jako kulečník nebo curling. Také tím vysvětlíme zpětný ráz při výstřelu z děla nebo explozi rachejtle na nočním nebi.
Moment síly
Působení síly na těleso může být posuvné a otáčivé. Zatímco posuvné účinky síly (\vec F) popisuje druhý Newtonův zákon, otáčivé účinky sil vyjadřuje tzv. moment síly.
Když fotbalista kopne do míče, míč se nejen rozletí ale také (často) začne rotovat.
Moment síly (značíme \vec M) je vektorová veličina. Čím má moment síly větší velikost, tím rychleji roztáčí těleso. Základní jednotkou momentu síly je jeden newtonmetr (Nm).
Velikost
Velikost momentu síly se počítá jako součin velikosti síly F a ramene síly r_\perp.
M=r_\perp \cdot F
Rameno síly není vždy vzdálenost síly od osy otáčení. Je to vlastně kolmá vzdálenost osy otáčení od přímky, ve které leží síla F. Lépe je to pochopitelné z obrázku 1. Zde jej značíme jako r_\perp (a vzdálenost od osy jako obyčejné r). Je to proto, že se v různých učebnicích značení liší (r, d, a, …).

Případně lze použít i ekvivalentního vztahu M=r F \sin (\alpha), kde \alpha je úhel mezi \vec F a \vec r.
Směr
Moment síly je kolmý na sílu i na rameno síly. Jeho směr se dá zjistit pomocí pravidla pravé ruky.
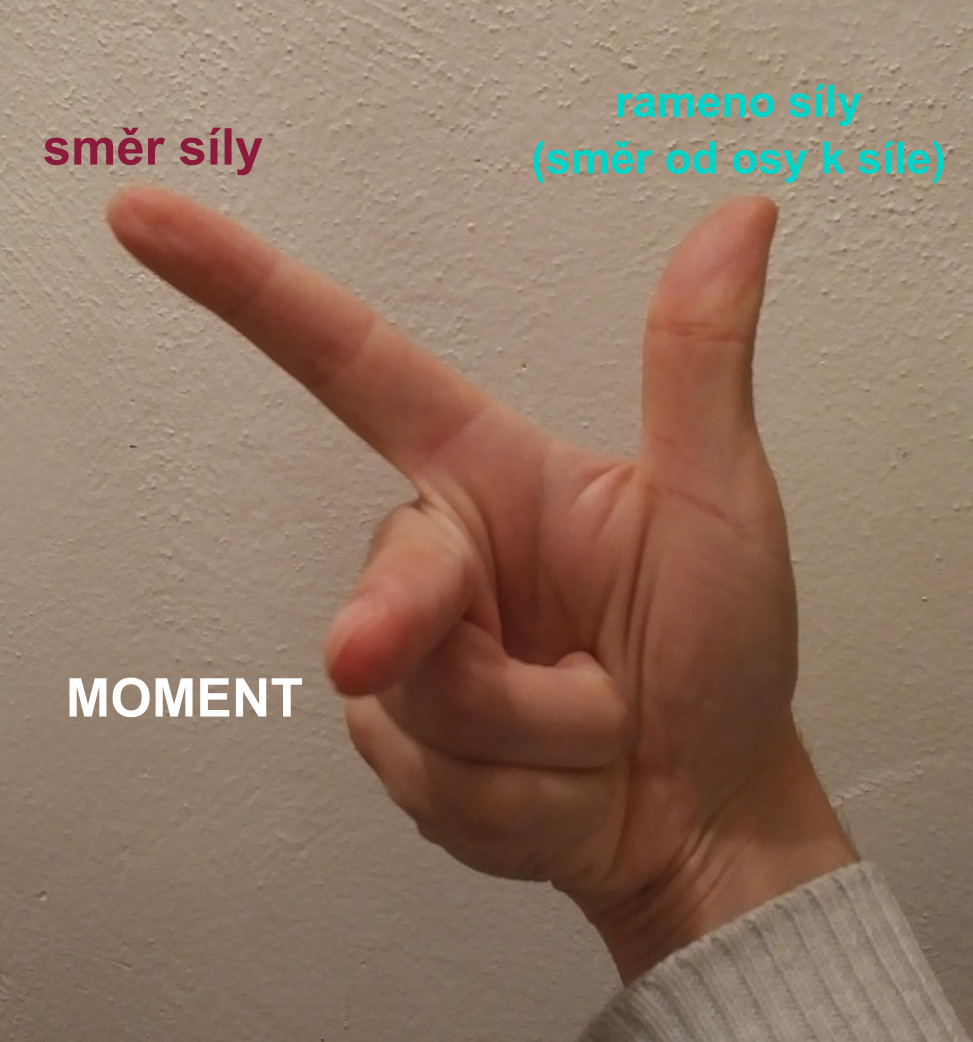
Protože je moment síly závislý na ose otáčení, znamená to, že jedna síla může mít různé momenty vůči různým osám (například vůči přednímu a zadnímu kolu bicyklu).
NahoruPráce, výkon, energie
Energii vnímáme jako míru schopnosti něco udělat. Stejně tak i ve fyzice – energie tělesa je definovaná jako jeho schopnost konat práci. Energie může mít různé formy a obecně se neztrácí, jen přeměňuje do jiných forem (její množství se zachovává).
- V mechanice se nejčastěji setkáme s energií pohybu nebo polohy, jinak řečeno kinetickou a potenciální.
- Součet kinetické a potenciální energie tělesa označujeme jako mechanickou energii tělesa.
- Když se přeměňují jen potenciální a kinetická energie tělesa nebo více těles mezi sebou, jde o zákon zachování mechanické energie.
Tělesa, která mají uloženou energii (např. pohybu), mohou vykonávat nějaké činnosti:
- Množství spotřebované (přeměněné) energie při vykonání úkolu odpovídá práci.
- Pokud konání práce trvalo nějakou dobu, můžeme určit jak rychle práce probíhala – rychlost výkonu práce je výkon.
- Ne vždy se všechna energie přemění na to co chceme (např. u žárovky se kromě svícení přemění spousta energie na teplo). Poměr mezi výkonem, který chceme a dodávaným výkonem (příkonem) je účinnost.
Kinetická a potenciální energie
Mechanickou energii dělíme na dvě části. Potenciální (polohovou) E_\mathrm p a kinetickou (pohybovou) E_\mathrm k.
Potenciální energie
Je v homogenním tíhovém poli Země úměrná výšce nad zemí h podle vzorce:
E_\mathrm p=mgh
Není jednoznačná. Záleží na definici nulové výšky (obvykle úroveň podlahy/země). Např. 0,5kg polštář může ze stejného okraje balkonu spadnout:
dovnitř balkonu (pak h\approx 1\,\mathrm m a E_\mathrm p\approx 5\,\mathrm J)
ven přes okraj a padat 4 patra dolů (pak dává smysl definovat nulovou výšku až na chodníku a tím pádem je h\approx 13\,\mathrm m s E_\mathrm p\approx 65\,\mathrm J).
Kinetická energie
Pro hmotný bod (nebo nerotující těleso) je úměrná druhé mocnině rychlosti:
E_\mathrm k=\frac{1}{2}mv^2
V klidu je tedy nulová. Protože se zvedá s druhou mocninou rychlosti, znamená to, že vůči rychlosti nejde o přímou úměru:
- rychlost v se zvýší na 2násobek → E_\mathrm k se zvýší na 2²násobek, tedy 4krát
- rychlost v se zvýší na 5násobek→ E_\mathrm k se zvýší na 5²násobek, tedy 25krát
- rychlost v klesne na 1/2 → E_\mathrm k klesne na 1/2²násobek, tedy na 1/4
Vůči hmotnosti ale o přímou úměru jde:
- hmotnost m se zvýší na 3násobek → E_\mathrm k vzroste na 3násobek
- hmotnost m klesne na 1/10 → E_\mathrm k klesne na 1/10
Takže jak se změní E_\mathrm k, když hmotnost klesne na třetinu, ale rychlost vzroste dvakrát? Musíme ji vynásobit součinem 1/3 krát 2². Tedy vzroste na \frac{4}{3}E_\mathrm k.
Kinetická energie balvanu
Balvan o m=10\,\mathrm{kg} se uvolnil a valí se z kopce.
- Na začátku má v=0\,\mathrm{m/s} proto je E_\mathrm k=0\,\mathrm J.
- Po chvíli se rozjede na v=2\,\mathrm{m/s} a má E_\mathrm k=\frac{1}{2}\cdot 10\cdot 2^2\,\mathrm J=20\,\mathrm J.
- Do údolí dorazí rychlostí v=4\,\mathrm{m/s} a tedy s kinetickou energií E_\mathrm k=\frac{1}{2}\cdot 10\cdot 4^2\,\mathrm J=80\,\mathrm J.
Když těleso rotuje má tato kinetická energie ještě jednu složku \frac{1}{2}J\omega^2, tou se zde ale nezabýváme, často ji totiž můžeme zanedbat.
NahoruMechanická energie tělesa a soustavy těles
Mechanická energie tělesa
Je rovna součtu kinetické a potenciální energie (E_\mathrm k a E_\mathrm p) tělesa. Značíme ji obvykle pouze jako E (pokud nepotřebujeme rozlišovat i jiné formy energie nebo další tělesa).
E=E_\mathrm k+E_\mathrm p
Mechanická energie parašutisty
Parašutista má v jednu chvíli E_\mathrm p=2400\,\mathrm J (vůči zemi) a E_\mathrm k=400\,\mathrm J
- Mechanická energie je E_\mathrm p+E_\mathrm k. Tedy 2400 J plus 400 J .
- Mechanická energie parašutisty je 2800 J.
Mechanická energie soustavy těles
Celkovou mechanickou energií soustavy těles je obyčejný součet mechanických energií jednotlivých těles. Mechanické energie jednotlivých těles píšeme s indexem tělesa (E_\mathrm {1}, E_\mathrm {2},…). Celkovou mechanickou energii pak bez indexu jen jako E.
E=E_\mathrm 1+E_\mathrm 2 +\cdots
Pokud rozepíšeme mechanické energie jednotlivých těles (např. E_1=E_\mathrm {k,1}+E_\mathrm {p,1}) může to vypadat také jako
E=E_\mathrm {k,1}+E_\mathrm {p,1}+E_\mathrm {k,2}+E_\mathrm {p,2}+\cdots
Mechanická energie akrobatů ve vzduchu
Jeden akrobat má mechanickou energii (součet svých E_\mathrm p+E_\mathrm k) rovnu 900 J. Druhý akrobat 1000 J a třetí 200 J.
- Celková mechanická energie soustavy je jejich součtem. Tedy 900+1000+200 J.
- Celková mechanická energie akrobatů je 2100 J.
Zákon zachování mechanické energie
Když se mechanická energie nepřeměňuje na jiné formy (např. na tepelnou energii třením), nebo když je tato přeměna zanedbatelná, můžeme použít zákon zachování mechanické energie (ZZME). Ten říká, že se mechanická energie v čase nemění (např. během pohybu, pružných srážek, …).
Jedno těleso
Pro jedno těleso to můžeme zapsat jako
E_\mathrm p+E_\mathrm k=\mathrm{konst.}
Takže o kolik se jedna složka energie zmenší, o to musí druhá vzrůst. Nejčastěji to můžeme využít u vrhů či pohybu tělesa po nakloněné rovině (bez tření).
Příklad: Padající tenisák
Tenisák o hmotnosti 0,1 kg upustíme z výšky 2 m na zem. Jaká je jeho kinetická energie 0,4 m nad zemí?
- Na začátku:
E_\mathrm p=mgh\approx 0{,}1\cdot 10\cdot 2\,\mathrm J=2\,\mathrm J
E_\mathrm k=\frac{1}{2}mv^2=0\,\mathrm J (nulová rychlost v)
celková mech. energie je tedy E=E_\mathrm k+E_\mathrm p=2\,\mathrm J
- 0,4 m and zemí:
E_\mathrm p=mgh\approx 0{,}1\cdot 10\cdot 0{,}4\,\mathrm J=0{,}4\,\mathrm J
Aby byl stále součet E_\mathrm k+E_\mathrm p roven 2 J, musela E_\mathrm k vzrůst o tolik, o kolik klesla E_\mathrm p. Tedy E_\mathrm k=1{,}6\,\mathrm J.
- Úpravou vzorce E_\mathrm k=\frac{1}{2}mv^2 bychom pak mohli vypočítat i rychlost (bez počítání rovnic volného pádu).
Příklad: Hod oštěpem
Jaké výšky mohl dosáhnout 1kg oštěp vržený E_\mathrm k=150\,\mathrm J pokud měl v nejvyšším bodě kinetickou energii jen E_\mathrm k=30\,\mathrm J?
- E_\mathrm p není zadaná, zřejmě je tedy na začátku hodu prakticky nulová.
- Snížení E_\mathrm k o 120 J musí podle E_\mathrm k+E_\mathrm p=\mathrm{konst.} znamenat E_\mathrm p=120\,\mathrm J.
- Z E_\mathrm p=mgh už snadno vyjádříme výšku h=\frac{E_\mathrm p}{mg}\approx\frac{120}{10}\,\mathrm m=12\,\mathrm m
Dvě a více těles
Pro izolované soustavy dvou a více těles platí, že se nemění celková mechanická energie. Například pro dvě tělesa to můžeme zapsat jako.
E_1+E_2=\mathrm{konst.}
nebo
E_\mathrm {p,1}+E_\mathrm {k,1}+E_\mathrm {p,2}+E_\mathrm {k,2}=\mathrm{konst.}
Mechanické energie jednotlivých těles se měnit mohou (např. po srážkách, vzájemným silovým působením). Setkáme se s ním u pružných srážek (např. kulečníkové koule) nebo pohybů vesmírných soustav.
Příklad: Kulečníkové koule
Jedna koule stojí. Druhá s kinetickou energií 2,5 J do ní narazí a zastaví se. Jakou kinetickou energii bude mít první koule?
- Všechny E_\mathrm p jsou stejné (vůči stolu nulové), můžeme je tedy z rovnic vynechat.
- Před srážkou: E_\mathrm {k,1}=0\,\mathrm J a E_\mathrm {k,2}=2{,}5\,\mathrm J. Takže E=E_\mathrm {k,1}+E_\mathrm {k,2}=2{,}5\,\mathrm J
- Po srážce: E_\mathrm {k,1}=? a E_\mathrm {k,2}=0\,\mathrm J
- Aby zůstal součet obou energií roven 2,5 J, musí být E_\mathrm {k,1} po srážce rovna právě 2,5 J.
Příklad: Kometa
Jak se změní rychlost komety při průletu kolem Slunce?
- I zde platí, že E_\mathrm p tělesa je tím menší, čím jsme blíž k zemi.
- Když se tedy kometa přibližuje ke Slunci její E_\mathrm p klesá (a E_\mathrm p Slunce také).
- Podle zákona zachování energie tedy musí vzrůst kinetické energie (Slunce i komety). A tedy i rychlost.
- Proto se rychlost komety při průletu kolem Slunce zvýší.
Práce (značíme W) je forma přenosu energie, proto má také stejnou jednotku, Joule.
V klasické mechanice se zabýváme především prací vykonanou působením síly na těleso po nějaké dráze. Práci ale koná jen ta část síly F, která je ve směru pohybu. Pro posun jedním směrem o s tedy můžeme psát:
W=F_\parallel\cdot s
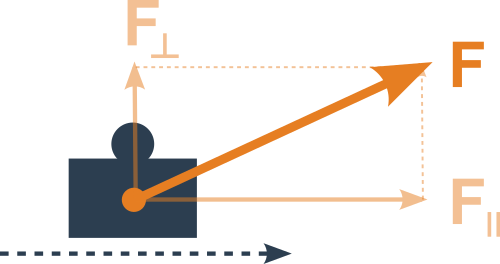
Pokud síla směřuje stejným směrem jako pohyb je to prostý součin W=F\cdot s
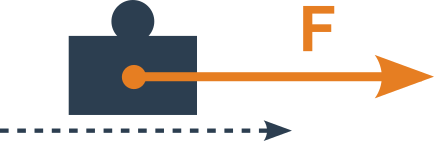
Pokud síla směřuje opačným směrem než pohyb, je práce záporná (W=-F\cdot s).

Pokud je síla kolmá na směr pohybu, je práce nulová.

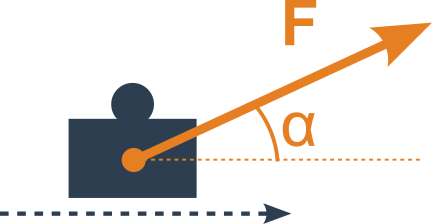
Zajímavosti
W=F\cdot s \cdot\cos\alpha
Výkon: základy
Veličina výkon v mechanice popisuje, jak rychle je konána práce W. Je definován doslova jako množství práce (W) za jednotku času (t). Značíme jej P, jeho jednotkou je watt (W).
Matematicky můžeme věty výše zapsat:
P=\frac{W}{t}
Ze vzorce výše můžeme odvodit i vztahy pro práci W=P\cdot t a čas t=\frac{W}{P}.
Čím větší je výkon, tím rychleji je práce konána (víc joulů práce za sekundu). U člověka odpovídá tomu, jak rychle se snažíme vykonat nějaký úkol, i když jej nemůžeme úplně ztotožnit s námahou (kvůli funkci kostry a svalů se namáháme i tehdy, když jen něco držíme a fyzikální práci prakticky nekonáme).
Protože se obvykle dozvíme jen množství práce za nějakou (delší) dobu, získáme takto průměrný výkon spíš než okamžitý.
Zde se procvičuje jen výkon spojený s mechanickou prací, existují ale formy spojené i s jinými přeměnami energie (elektrický výkon, tepelný výkon, …). Toho mechanického dokáže člověk snadno vyvinout i stovky wattů W. Vysavač třeba 1000 W. A auto třeba 100 kW.
Výkon tahače saní
Jaký průměrný výkon podal člověk který taháním saní vykonal práci 100 J za 20 s?
- Výkon je práce děleno čas.
- Tedy P=\frac{W}{t}
- Dosadíme práci 100 J a čas 20 s.
- Výkon byl tedy 5 W. (sáňky asi dobře klouzaly).
Výkon výtahu
Jaký výkon má výtah, který za 8 s vyveze 2kg náklad o 4 m nahoru?
- Když něco zvedáme, zvýší se polohová energie o E=mgh. Toto zvýšení energie odpovídá práci.
- Práce W je tedy rovna E=mgh\approx 2\cdot 10\cdot 4\,\mathrm J=80\,\mathrm J.
- Čas je 8 s.
- Dosadíme do P=\frac{W}{t}.
- Výkon byl tedy 80 děleno 8 wattů. Tedy 10 wattů.
Pokud za práci dosadíme práci nějaké tažné síly F na dráze s, dostaneme pro výkon nakonec vztah P=F\cdot v. Tomu se věnujeme v samostatném cvičení Výkon síly konající práci.
NahoruVýkon síly konající práci
Pokud je výkon P je roven práci W dělené časem t. Můžeme ale za práci dosadit konkrétně. Třeba práci síly během pohybu po určité dráze, tedy W=F_\parallel \cdot s. (pro další text předpokládejme, že je síla F leží ve směru pohybu, tedy místo F_\parallel \cdot s budeme psát přímo F\cdot s).
Dosadíme do P=\frac{W}{t}:
P=\frac{F\cdot s}{t}
Jenže s/t (dráha za čas) je definice rychlosti v. Proto je výkon takové síly roven:
P=F\cdot v
Tedy výkon je součinem síly pohonu a rychlosti. Může být jinak značena (např F_1, F_\mathrm{motoru}, …). Nejde tedy automaticky o výslednici sil.
- Autíčko je poháněno vpřed silou 20 N a jede 2 m/s . Výkon pohonu je 20 krát 2 wattů. Tedy 40 W.
- Saně táhneme vpřed silou 15 N, brzdí nás tření 10 N a jdeme rychlostí 1 m/s . Výkon tažné síly je 15 krát 1 wattů (odporová síla nás nezajímá). Tedy 15 W.
Tento vzorec snadno upravíme na vzorce pro velikost síly F=\frac{P}{v} nebo rychlosti v=\frac{P}{F}.
- Cyklista dává do šlapátek výkon 100 W a jede rychlostí 10 m/s. Podle F=\frac{P}{v} tedy pohání kolo silou 100/10 newtonů. Tedy 10 N.
Zajímavější jsou ale jeho důsledky. Například spousta motorů má konstantní výkon (nebo konstantní maximální výkon). Podle P=F\cdot v musí být pak konstantní i součin F\cdot v. Takže při zvýšení rychlosti bude hnací síla motoru se stálým výkonem klesat. Třeba i do té míry, že odporové síly pohybu se jí vyrovnají a výslednice sil bude nulová, nebo dokonce bude mít opačný směr.
Druhá výhoda vztahu P=F\cdot v je, že pokud dosadíme okamžitou rychlost v dostáváme jako výsledek okamžitý výkon. To s prací obvykle uváděnou za nějakou dobu a časovým intervalem nešlo (získávali jsme jen průměrný výkon za tento čas).
NahoruÚčinnost a příkon
Účinnost je číslo od 0 do 1 (popř. od 0 % do 100 %), které vyjadřuje, jakou část dodávaného výkonu dokáže spotřebič využít k vykonávání své funkce. Skutečná účinnost nemůže být vyšší než 100 % (takové zařízení by vyrábělo energii z ničeho – perpetuum mobile).
Účinnost značíme řeckým písmenem η (éta). Je bezrozměrná (jednotkou je 1).
Dodaný výkon označujeme jako příkon a značíme P_0. Využitý výkon označujeme prostě jako výkon (spotřebiče) a značíme P.
Matematicky zapíšeme účinnost jako \eta = \frac{P}{P_0}.
Úpravou odvodíme také vztahy pro výpočty výkonu P=\eta\cdot P_0 a příkonu P_0 = \frac{P}{\eta}.

Příklad: žárovka
- Žárovka odebírá ze zásuvky příkon 80 W. Na očekávanou světelnou energii se přemění ale jen 12 W.
- Zbytek výkonu se přemění hlavně na teplo, ale kvůli topení žárovku nepoužíváme.
- Účinnost tedy je jen \eta=12/80=0{,}15= 15\,\%.
Příklad: rychlovarná konvice
- Rychlovarná konvice odebírá 2000 W. Skoro všechnu energii přeměňuje na teplo, ale jen 1900 W tepelného výkonu ohřívá vodu.
- Zbytek tepelného výkonu ohřívá např. konstrukci konvice, nebo okolní vzduch (což nepotřebujeme). Malá část příkonu je navíc přeměněna na elektromagnetickou energii.
- Účinnost tedy je \eta=1900/2000=0{,}95= 95\,\%.
Zajímavosti
Některé stroje se chlubí účinností přes 100 % (např. kondenzační kotel). Ale nebojte, fyzikální zákony stále platí – energie se nedá vyrobit z ničeho. Hodnota přes 100 % je způsobena prostě tím, že výrobce do příkonu P_0 nezapočítal veškerou energii obsaženou v palivu, ale jen jeho tzv. výhřevnost. Energii ve spalinách (kterou kondenzační kotle umí využít) zkrátka přehlíží.
Princip páky je jedním z nejpraktičtějších využití momentu síly. Páka nám usnadňuje některé věci, na které bychom normálně neměli dostatečnou sílu, například rozlousknout ořech.
Páka a síly
Mějme těleso, které se může otáčet kolem nějaké osy nebo opěrného bodu (kleště, houpačka, zahradní kolečka). Sílu působící na jednom místě F_1 (např. tíhu nákladu) můžeme vyrovnávat druhou silou F_2 a držet páku v rovnováze. Síly působí ve vzdálenostech od osy r_1 a r_2 a nemusí být stejně velké.
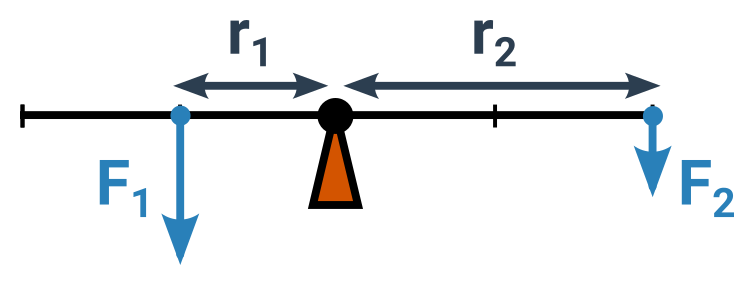
V rovnováze je poměr velikostí sil opačný než poměr jejich ramen. Zde procvičíme jednodušší případ, kdy jsou síly kolmé na úsečky r_1 a r_2. Pak je ramenem síly přímo vzdálenost od osy. Pak platí, že v rovnováze je poměr velikostí sil opačný než poměr jejich vzdáleností od osy.
F_1:F_2=r_2:r_1
Pozn.: Ve cvičeních je grafika sil pouze ilustrační – délka šipek neodpovídá velikosti sil.
Příklad: Kdy budou síly v rovnováze stejně velké?
Síly v rovnováze nemusí být stejně velké. Ale kdy stejně velké budou?
- Platí F_1:F_2=r_2:r_1.
- Pokud jsou obě síly stejně velké, je F_1:F_2 rovno jedné.
- Jednička tedy musí být i poměr r_2:r_1.
- To znamená, že obě vzdálenosti musí být stejné.
Páka a hmotnosti
Když nepočítáme se silami, ale s hmotnostmi, platí pro rovnováhu obdobný vztah.
m_1:m_2=r_2:r_1
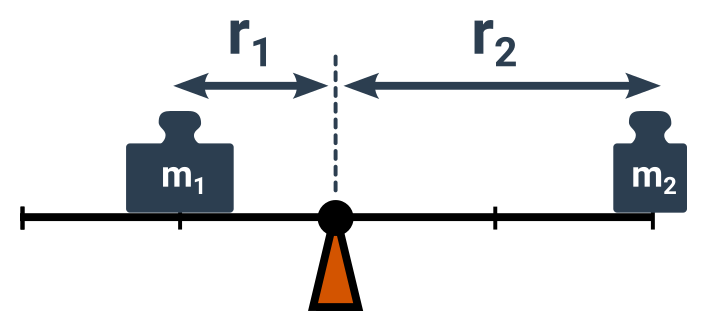
Příklad: Na houpačce
Kdo musí na houpačce sedět víc u středu, aby se mohli pohodlně houpat? Maminka nebo holčička? 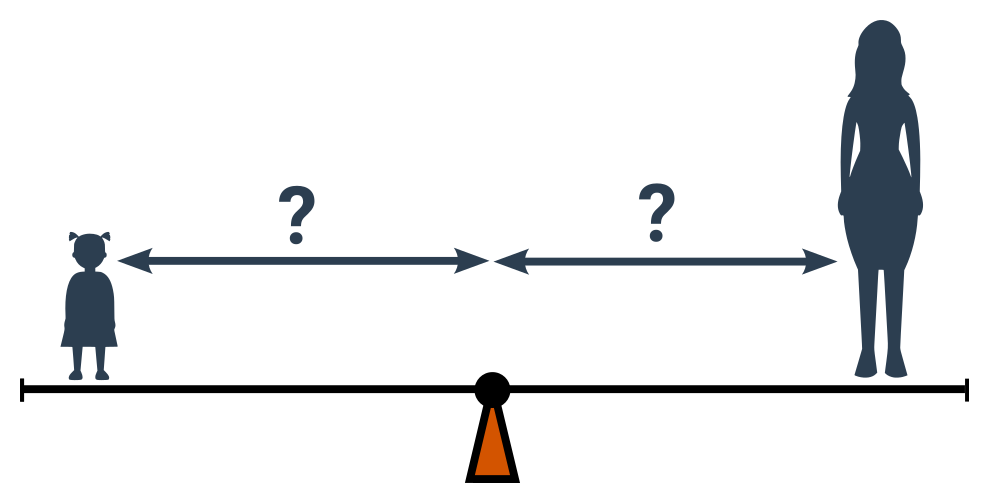
- Rovnováha (a snadné houpání) nastane, když jsou vzdálenosti v opačném poměru než hmotnosti (m_1:m_2=r_2:r_1).
- Holčička má menší hmotnost.
- Holčička tedy musí mít větší vzdálenost od středu.
- Blíže ke středu si tedy bude muset sednou maminka.
Síly a hmotnosti dohromady
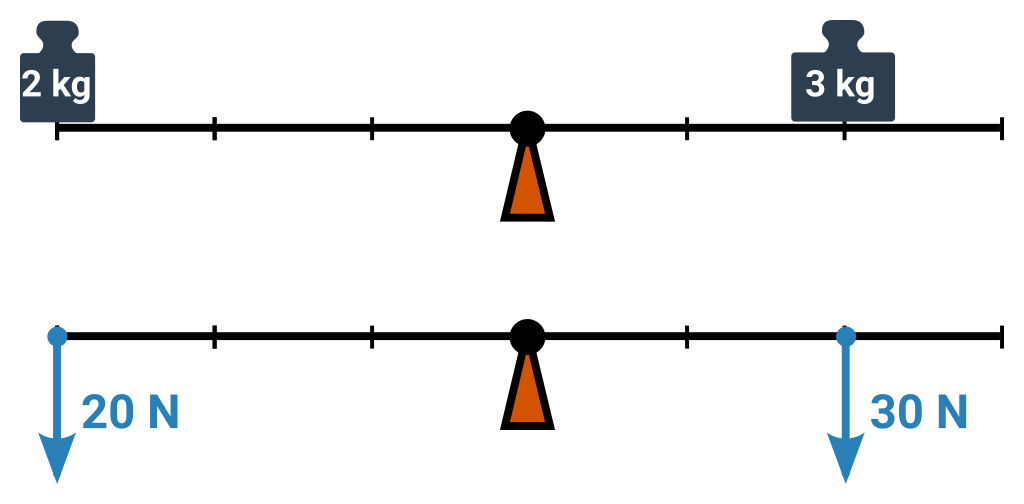
Pokud kombinujeme hmotnost a síly, musíme hmotnosti převést na tíhové síly. Každý kg odpovídá síle asi 10 N. Bedna o 3 kg, tedy bude působit silou 30 N. Člověk s 85 kg pak silou 850 N.
Příklad: Naložený trakař
Jakou silou musíme zvedat řídítka trakaře? 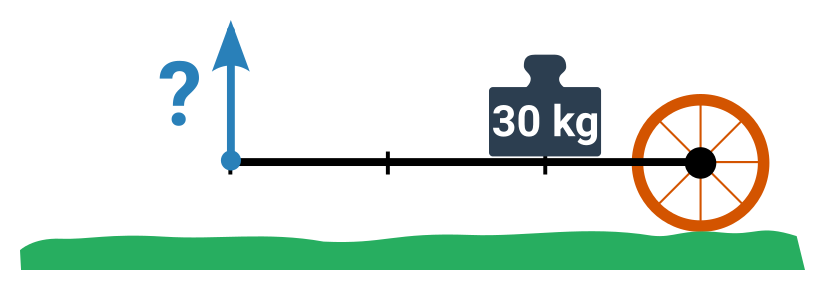
- Kombinujeme sílu a hmotnost. Musíme tedy nejprve převést hmotnost trakaře na tíhovou sílu.
- 30 kg znamená tíhovou sílu 300 N.
- Platí F_1:F_2=r_2:r_1 – síly musí mít opačný poměr než vzdálenosti do osy.
- Poměr vzdáleností r_2:r_1 je 3 ku 1. Tedy zvedáme trakař v trojnásobné vzdálenosti od osy.
- Poměr sil tedy bude 1 ku 3. Bude tedy stačit třetinová síla (vůči těm 300 N).
- Zvedat musíme silou 100 N.
Druh páky
Pokud působí všechny síly na jedné straně od osy otáčení jde o jednozvratnou páku (osa otáčení je pak obvykle na kraji, např. pinzeta, trakař). Pokud působíme silami na opačných stranách od osy otáčení, jde o dvojzvratnou páku (např. kleště, nůžky, houpačka).
Proč platí podobné vztahy pro hmotnosti i síly?
- Díky přímé úměře tíhy závaží a hmotnosti (F=m g).
- Konstanta g je pro všechna závaží stejná.
- Dosadíme za F_1 a F_2 do rovnice F_1:F_2=r_2:r_1.
- Dostaneme (m_1g):(m_2g)=r_2:r_1.
- Protože m_1g:m_2g je vlastně zlomek, můžeme v něm krátit konstantu g.
- Dostaneme m_1:m_2=r_2:r_1.
Kladka je v podstatě upevněné nebo zavěšené kolečko, které pomocí lanka nese nějaký náklad. Systém kladek se nazývá kladkostroj. Kladky dělíme na pevné (1) a volné (2).
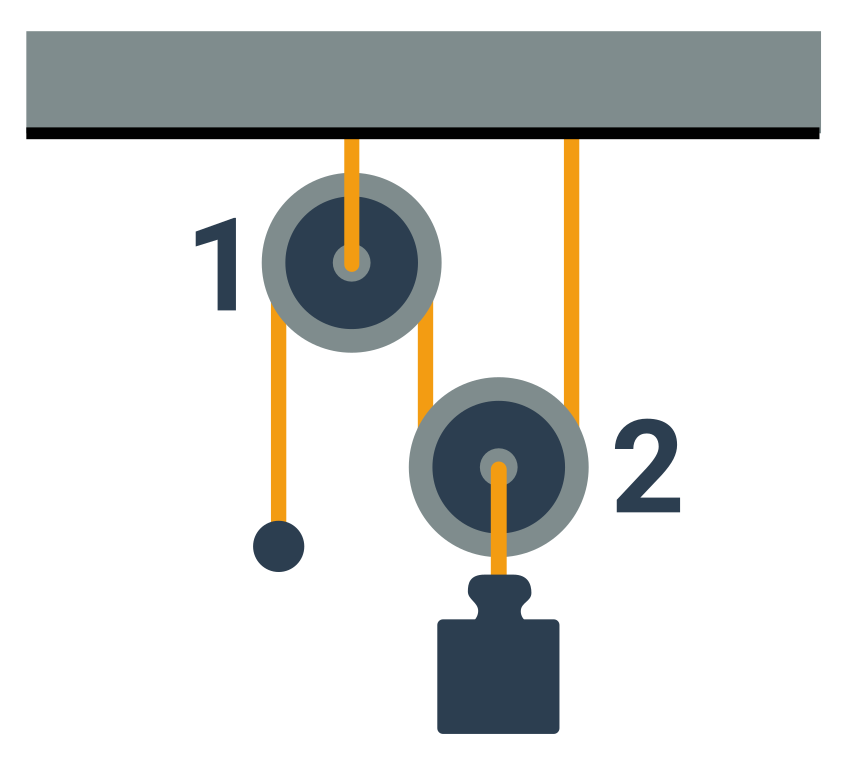
Pevná kladka se nemůže při zatáhnutí za lano hýbat. Volná se naopak bude pohybovat nahoru a dolů podle toho, jak se lanko, které ji nese, zkracuje či prodlužuje.
Kladky a kladkostroje fungují podobně jako páky (tedy umožňují unést těžký náklad pomocí malé síly). Navíc ale přidávají přenos směru síly. Tedy (otočením lanka přes kolečko) umožňují např. zvedat kyblík pomocí síly směřující dolů. Nebo šikmo.
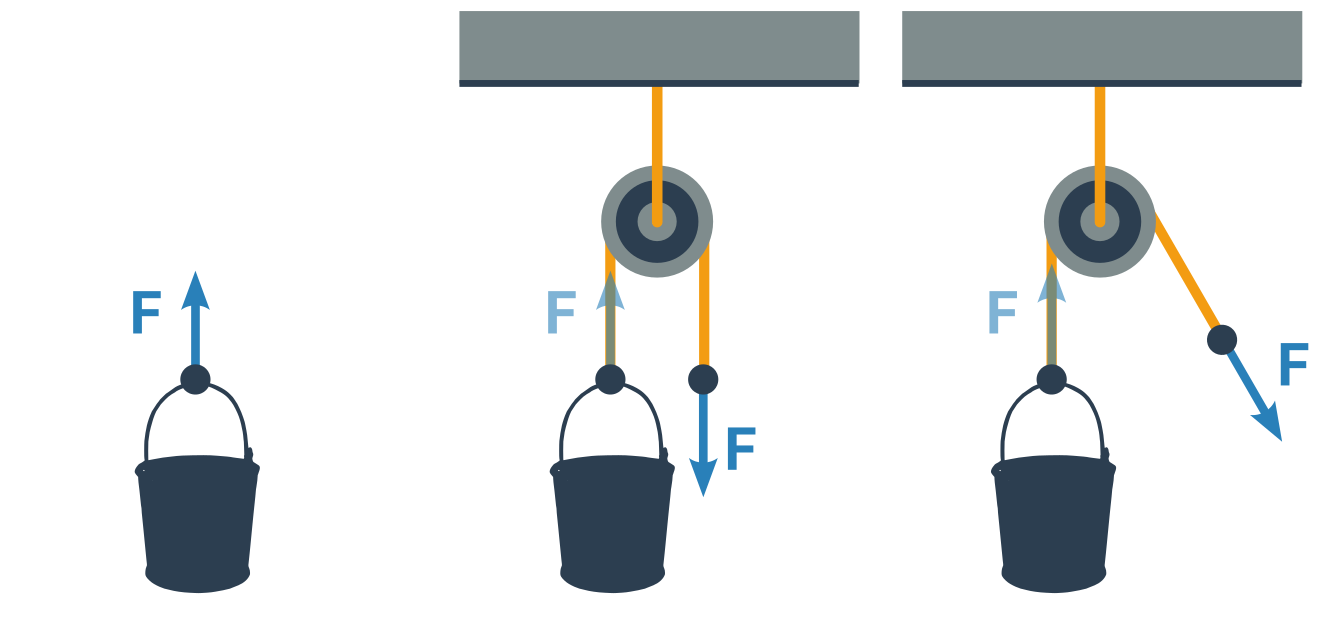
Pevná kladka
Otáčí se na ose v pevné konstrukci, nebo je osa zavěšena na laně, které má neměnnou délku.
Kolečko kladky je vlastně rovnoramenná páka. Obě vzdálenosti od osy jsou stejné a proto je velikost síly na obou stranách kolečka v rovnováze stejná. Pevná kladka tedy pouze přenáší směr síly po laně.
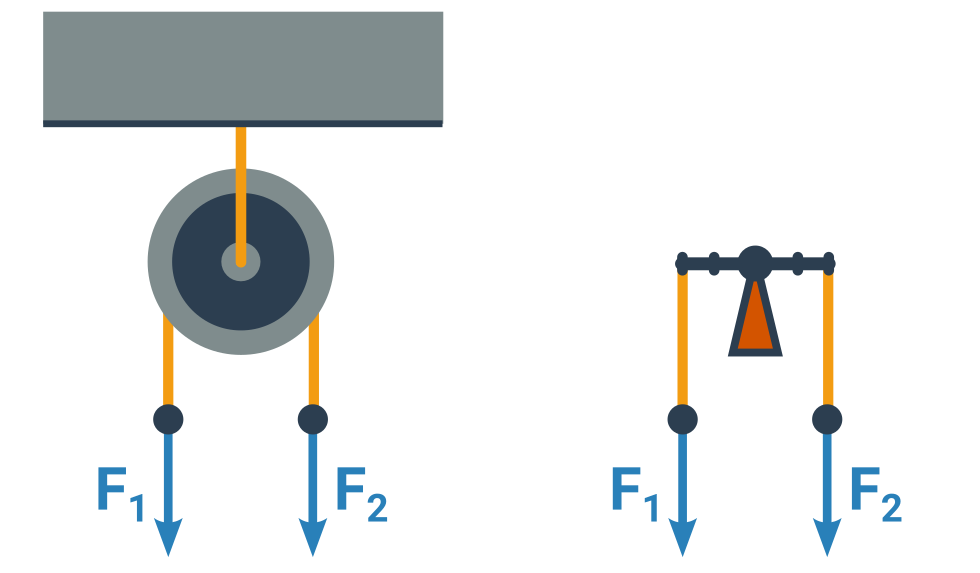
Volná kladka
Kladka zavěšená na pohyblivém laně funguje také jako páka, takže síly, které ji z obou stran táhnou nahoru, musí být stejné. Zároveň ale v rovnováze musí viset ve vzduchu a nepadat. Součet těchto sil tedy musí být stejný jako tíha, kterou kladka nese na své ose (aby výsledná síla byla 0).
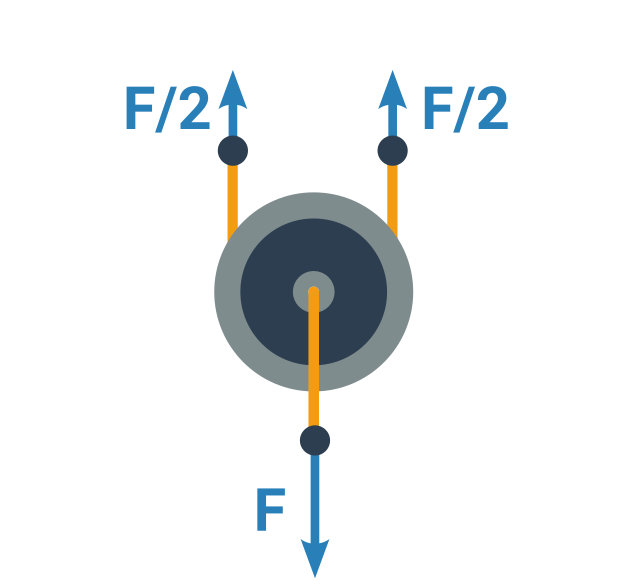
Každá volná kladka tedy zmenšuje sílu, kterou musíme za jeden konec lanka tahat, na polovinu.
Příklad: Síly na volné kladce
Nese volná kladka větší tíhovou sílu závaží, než kterou taháme za volný konec lana v drážce? (kladka se nehýbe)
- Podle obrázku výše musí být síly tahající za každý konec lana v drážce poloviční, než tíhová síla závaží.
- Na kladce tedy visí dvakrát tak síla, než kterou taháme.
- Odpověď je ano – tíhová síla je větší (dvojnásobná).
Příklad: Závaží na volné kladce
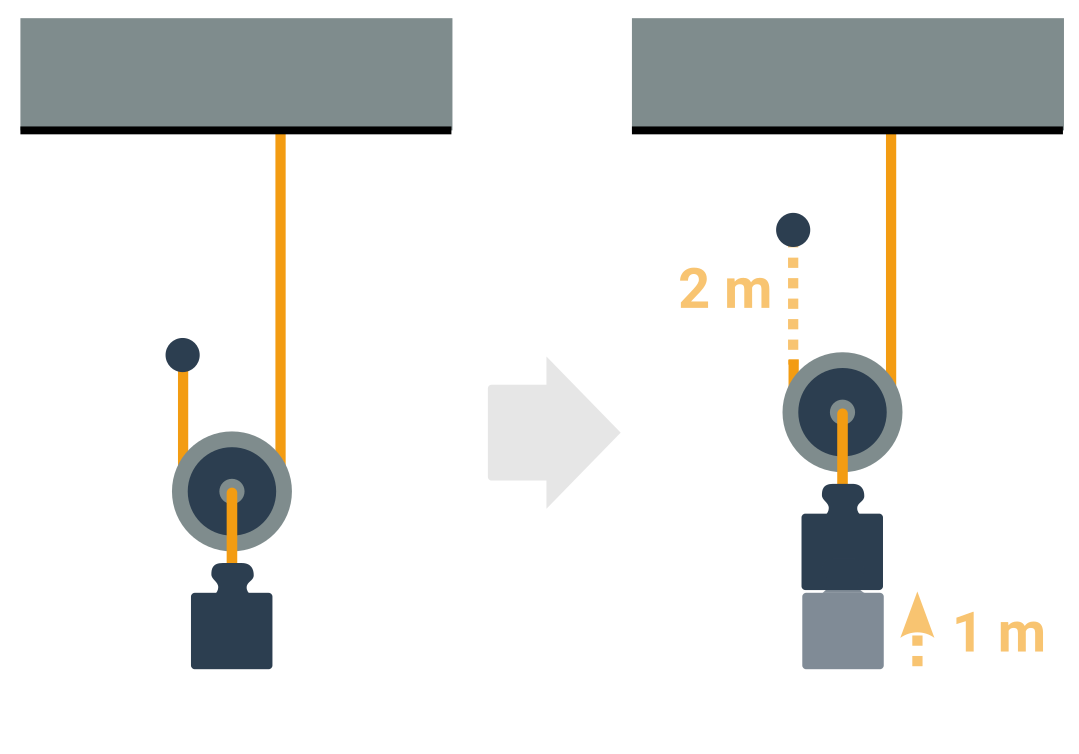
Obrázek ukazuje postup při zjištění síly, která drží kladku nahoře:
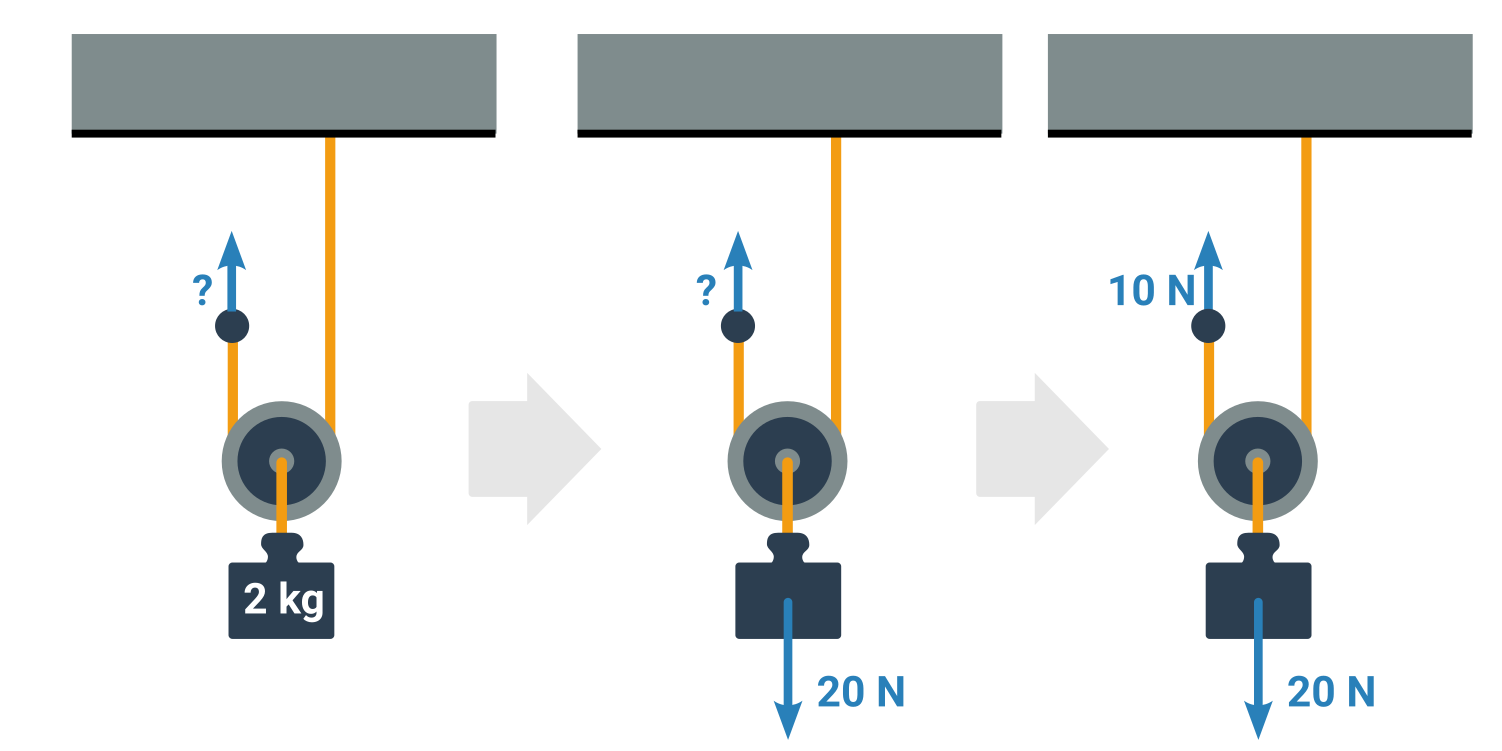
- Nejprve převedeme hmotnost závaží na tíhovou sílu. Stejnou silou musí ostatní lana kladku nést.
- Poté uplatníme pravidlo dělení sil nesoucích volnou kladku napůl.
- Vyjde nám 10 N.
Zároveň ale pro zvednutí závaží na volné kladce o určitou výšku taháme dvojnásobnou délku lana (protože se musí zkrátit lano na obou stranách kolečka).
Kladkostroj
Je kombinace více kladek. Pokud rozložíme síly zátěže na volných kladkách, můžeme potřebnou sílu zmenšit i mnohonásobně.
Příklad: Závaží v kladkostroji
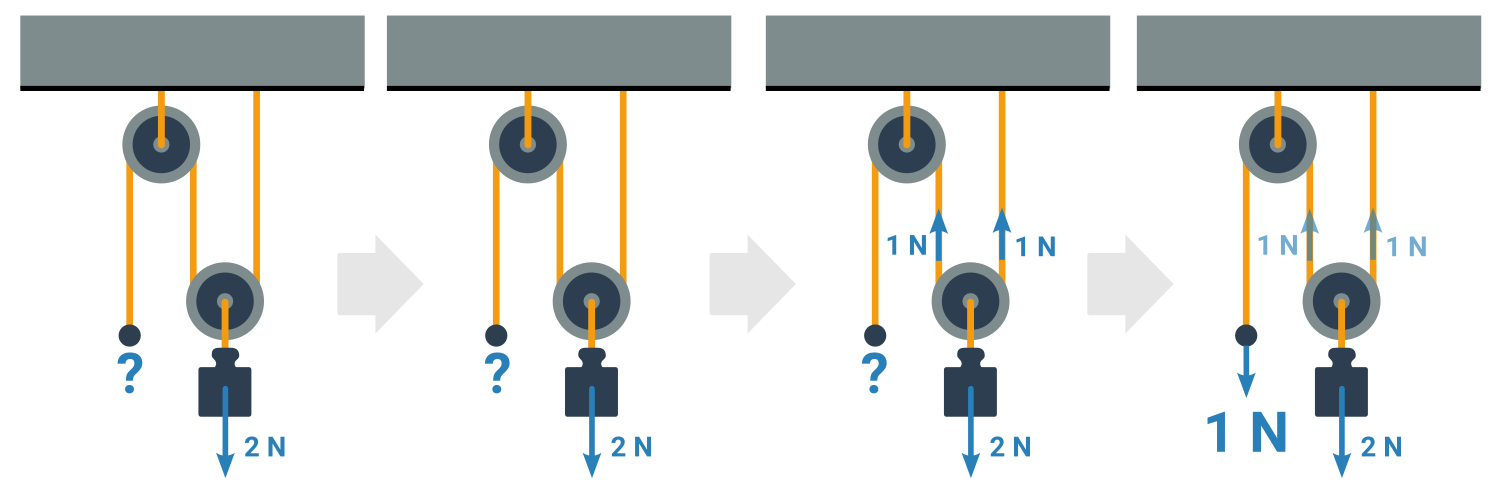
Mechanika kapalin a plynů
Důležitou roli v mechanice kapalin a plynů hraje tlak. Obecně tento tlak můžeme rozdělit na
tlak vyvolaný (gravitační) tíhou samotné tekutiny (hydrostatický tlak u kapalin a atmosférický tlak u plynů)
tlak vyvolaný působením vnější síly na tekutinu v uzavřené nádobě (popisuje Pascalův zákon).
Celkový, nebo také absolutní tlak je pak součtem těchto dílčích tlaků.
1. Tlak vyvolaný tíhou tekutiny
Pokud něco neseme na hlavě, například těžký klobouk, cítíme jak na nás působí jeho tíha (neseme jej). Pokud si ale stoupneme my na klobouk (nezkoušejte!), jeho tíhu necítíme.
Podobně působí na tělesa ponořená v tekutině i tíha této tekutiny. A stejně jako v analogii s kloboukem je rozhodující jen ta část tekutiny, která se nachází nad tělesem. Projevem takového působení je tedy tlak tekutiny, který bude tím větší čím hlouběji je těleso ponořeno (tlačí větší sloupec tekutiny).
2. Tlak vyvolaný působením vnější síly
Je určen silou F a plochou S (například pístu), na kterou tato síla působí. Přenáší se do celého objemu kapaliny a je v celém tomto objemu stejný.
Toho využívají hydraulická zařízení, která fungují podobně jako jednoduché stroje. Pomocí různě velkých pístů převádíme sílu, takže například dokážeme sami zvednout auto (hydraulický zvedák).
NahoruHydrostatický tlak: základy
U kapalin je projevem jejího tíhového působení hydrostatický tlak. Jeho působením na plochu je hydrostatická tlaková síla.
Hydrostatický tlak značíme p_\mathrm h a závisí na hloubce pod hladinou h, přitažlivosti planety (tíhové zrychlení g) a na tom, o jak těžkou kapalinu jde (hustota \rho). Je to přímo součin:
p_\mathrm h=h\cdot\rho\cdot g
Hlavní rozdíl vůči tlaku vyvolanému vnější silou je ten, že není v celém objemu kapaliny stejný (roste s hloubkou).
Příklad: Tlak na dně bazénu
Plavecký bazén má hloubku 1,5 m. Jaký je hydrostatický tlak u dna?
- Chceme určit p_\mathrm h a známe hloubku bazénu h.
- Protože v zadání není nic navíc, máme nejspíš předpokládat, že se bazén nachází na Zemi a použijeme obvyklou hodnotu g\approx 10\,\mathrm{m/s^2}. Také bude asi napuštěn vodou a ne kyselinou. Tedy přibližně \rho\approx 1000\,\mathrm{kg/m^3}.
- Můžeme tedy dosadit do p_\mathrm h=h\cdot\rho\cdot g.
- p_\mathrm h=1{,}5\cdot 1000\cdot 10 \,\mathrm{Pa}=15 000\,\mathrm{Pa}.
- Hydrostatický tlak na dně je tedy 15 000 Pa.
Příklad: Mumie ponořená ve rtuti
Jaký hydrostatický tlak by drtil zlou filmovou mumii 1 m pod hladinou rtuti (hustota 13 500 kg/m³)?
- Hloubka h je 1 m a tíhové zrychlení g je přibližně 10 m/s².
- Jako \rho musíme použít hustotu rtuti (ne vody), tedy 13 500 kg/m³
- Dosadíme: p_\mathrm h=h\cdot\rho\cdot g= 1\cdot 13 500\cdot 10 \,\mathrm{Pa}=135 000\,\mathrm{Pa}.
- Stvůru tedy drtí 135 000 Pa.
Podle známé definice tlaku jako síly na plochu (p=F/S) můžeme odvodit i vzorec pro sílu vyvolanou hydrostatickým tlakem (působící na plochu S).
Do vzorce F=p\cdot S stačí jen dosadit hydrostatický tlak p_\mathrm h:
F= S \cdot h\cdot \rho\cdot g
Příklad: Síla na tělo potápěče
Jaká síla drtí tělo (1,8 m²) potápěče v hloubce 50 m pod vodou?
- Síla je F=p_\mathrm h\cdot S.
- Plochu S známe a z p_\mathrm h=h\cdot\rho\cdot g máme hloubku h. Za g a \rho dosadíme obvyklé hodnoty 10\,\mathrm{m/s^2} a 1000\,\mathrm{kg/m^3} (voda).
- Dosadíme F= S \cdot h\cdot \rho\cdot g = 1{,}8\cdot 50\cdot 1000\cdot 10\,\mathrm N
- Po vyčíslení dostaneme 900 000 N. Tedy 0,9 meganewtonu.
Zajímavosti
- Už v hloubce 10 m pod vodu je hydrostatický tlak stejně velký jako tlak celé atmosféry Země.
Archimédův zákon: intuitivně
Základní znění
Těleso ponořené do kapaliny je nadlehčováno vztlakovou silou. Její velikost se rovná velikosti tíhy kapaliny stejného objemu, jako je objem ponořené části tělesa.
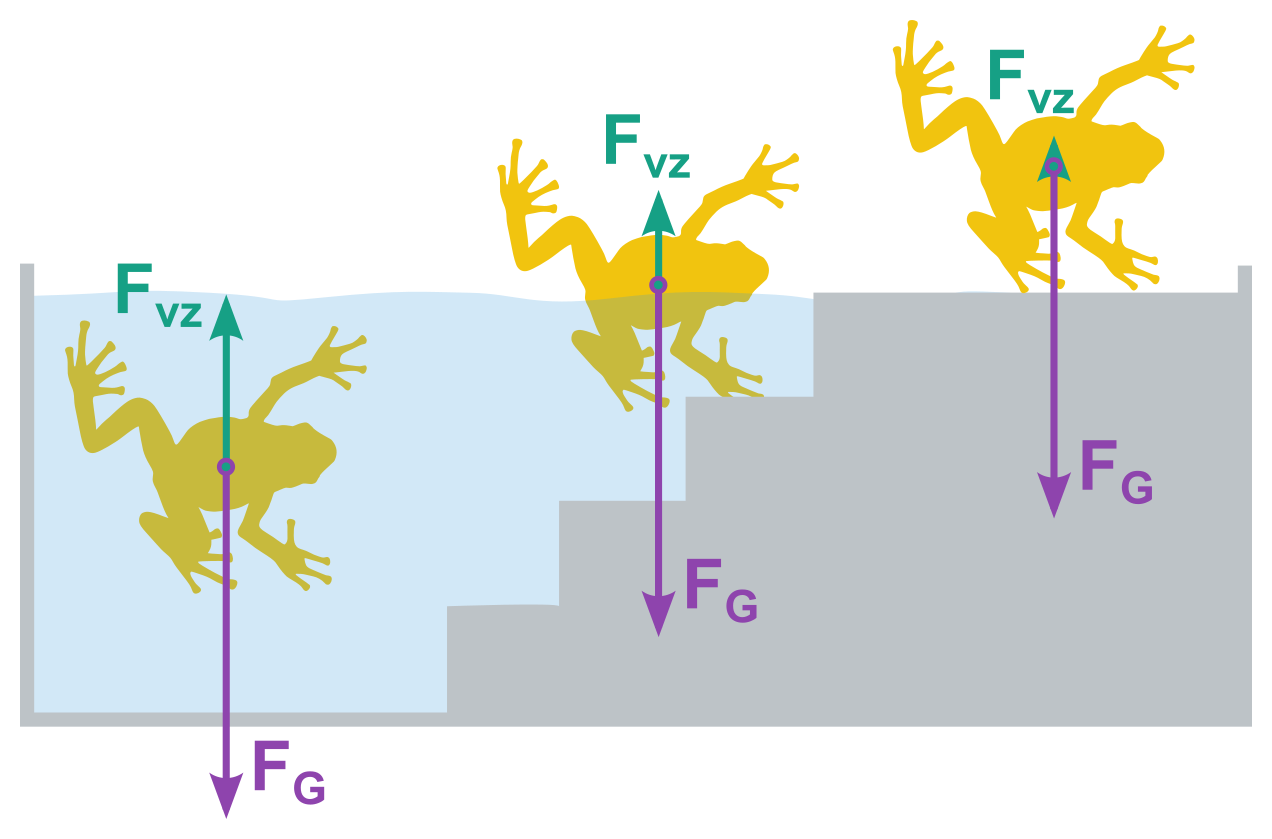
Platí jak pro kapaliny, tak pro plyny. Velikost vztlakové síly (F_\mathrm{vz}) je v plynech výrazně menší než v kapalinách kvůli jejich nižším hustotám.
F_{\mathrm{vz}} = V_{\mathrm{pod}} \cdot \rho_{\mathrm K} \cdot g
kde je g velikost tíhového zrychlení, V_{\mathrm {pod}} objem ponořené části tělesa a \rho_{\mathrm K} hustota kapaliny (případně plynu).
Těleso plovoucí po vodní hladině
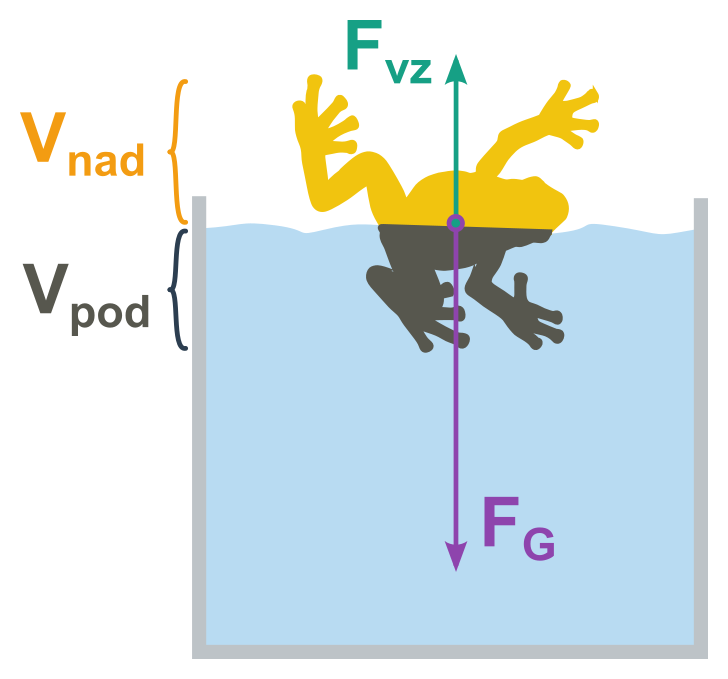
Pro těleso plovoucí po hladině lze odvodit vztah mezi hustotami tělesa a kapaliny:
\frac{V_{\mathrm {pod}}}{V_{\mathrm {nad}} + V_{\mathrm {pod}}} = \frac{\rho_{\mathrm T}}{\rho_{\mathrm K}}
(\rho_{\mathrm T} je hustota tělesa, \rho_{\mathrm K} je hustota kapaliny, V_{\mathrm {pod}} je objem ponořené části tělesa a V_{\mathrm {nad}} + V_{\mathrm {pod}} = V je celkový objem tělesa.)
Příklady a využití Archimédova zákona
Archimédův zákon se uplatňuje v plynném prostředí, ale zejména v kapalném prostředí. Díky Archimédovu zákonu létají pouťové balonky i vzducholodě, na moři se nepotopí lodě, ponorky a ryby mohou ovlivňovat svůj pohyb ve vertikálním směru.
Tíha tělesa
- Při plavání určitě cítíte, že vás voda nadnáší. Vztlaková síla totiž působí na všechna tělesa – jak ve vodě, tak ve vzduchu.
- Proto když měříme „hmotnost“, zjistíme „váhu“ tělesa. Ta se od skutečné hmotnosti právě o tu nadlehčenou část.
- Rozdíl je ve vzduchu (\rho\approx 1{,}23\,\mathrm{kg/m^3}) jen nepatrný, ve vodě (\rho\approx 1000\,\mathrm{kg/m^3}) jej ale poznáme.
Pohyb pod vodou ve svislém směru
Archimédova zákona využívají k vertikálnímu pohybu ve vodě ryby. Jsou totiž vybaveny plynovým měchýřem.
Při pohybu ↑ jej nafouknou, a tím vzroste jejich V a tedy i F_\mathrm{vz}.
Při pohybu ↓ jej zase vyfouknou a F_\mathrm{vz} klesne.Stejně to děláme i my při potápění s bombou. Když se více nadechneme a nafoukneme plíce stoupáme vzhůru, když dýcháme mělce klesáme.
- Podobný princip využívají ponorky, ve kterých jsou instalovány vzduchové komory. Během ponoru jsou tyto komory naplněny vodou, a tedy je ponorka tažena dolů. Pro výnor se komory naplní vzduchem, čímž se její hmotnost výrazně sníží a velikost vztlakové síly převýší velikost síly tíhové.
Pohyb ve vzduchu ve svislém směru
- Letecké stroje využívají toho, že je jejich průměrná hustota menší než hustota vzduchu. Poznáme je hlavně díky tomu, že největší objem zaujímá vak nebo plynová nádrž.
- Vzducholodě byly plněny plynem s menší hustotou než vzduch, tedy vodíkem (v dnešní době se již nevyužívá), nebo heliem. Horkovzdušný balón zase využívá řídkého horkého vzduchu.
Zajímavosti
- Nezáleží na tom, jaký objem těleso vytlačilo vzhůru. Jelikož hydrostatický tlak závisí pouze na hloubce kvůli hydrostatickému paradoxu, je nejdůležitější objem ponořené části tělesa.
Atmosférický tlak
Pro tíhové působení plynů naší (nebo jiné) atmosféry definujeme atmosférický tlak. Princip je podobný jako u hydrostatického tlaku. I atmosférický tlak závisí na přitažlivosti (tíhovém zrychlení g), výšce atmosféry a její hustotě. Nemůžeme ale jednoduše použít stejný vzorec jako pro hydrostatický tlak, protože hustota plynu \rho není konstantní, výška atmosféry není jasně ohraničená a dokonce i g není v 60km výšce stejné jako u hladiny moře.
Platí alespoň, že čím výše se nacházíme, tím nižší atmosférický tlak tam bude (menší část vzduchového sloupce nad námi). Rozdíly se ale projeví až na větších výškových rozdílech, i kvůli malé hustotě vzduchu \rho\approx 1{,}2\,\mathrm{kg/m^3}.
U hladiny moře počítáme s tlakem kolem 100 000 Pa. Standardní hodnota je stanovena na 101 325 Pa. Znamená to také, že podle F=p\cdot S nám na 1 m² kůže působí síla 101 325 N. Naštěstí stejná síla působí i zevnitř těla (např. plíce), takže nejsme slisováni do malých masových kuliček.
Kromě pascalů se používají jednotky jako bar (1 bar = 100 000 Pa), atmosféra (1 atm. = 101 325 Pa) Často se atmosférický tlak také uvádí v neobvyklém násobku – hektopascalech (hPa).
Rozdíly v atmosférickém tlaku z velké části tvoří počasí (tlakové výše a níže, přesun vzduchu mezi nimi a vznik větru).
NahoruRovnice kontinuity
U proudění tekutin definujeme tzv. objemový průtok Q_V. Je to objem tekutiny, který proteče trubkou za jednotku času. Jednotkou je tedy m³/s a platí:
Q_V=\frac{V}{t}
Příklad: ropovod
Jaký byl průtok ropovodem, pokud za 1 minutu proteklo 30 m³ ropy?
- Známe V i t.
- Čas t není v základních jednotkách, musíme jej tedy převést na sekundy t= 60\,\mathrm s
- Dosadíme do Q_V=V/t
- Q_V=30/ 60 \,\mathrm {m^3/s}=0{,}5 \,\mathrm {m^3/s}.
- Průtok je 0{,}5 \,\mathrm {m^3/s} ropy.
Objem V je ale roven součinu průřezu trubice S a posunu kapaliny o dráhu s. Po dosazení máme Q_V=\frac{S\cdot s}{t}.
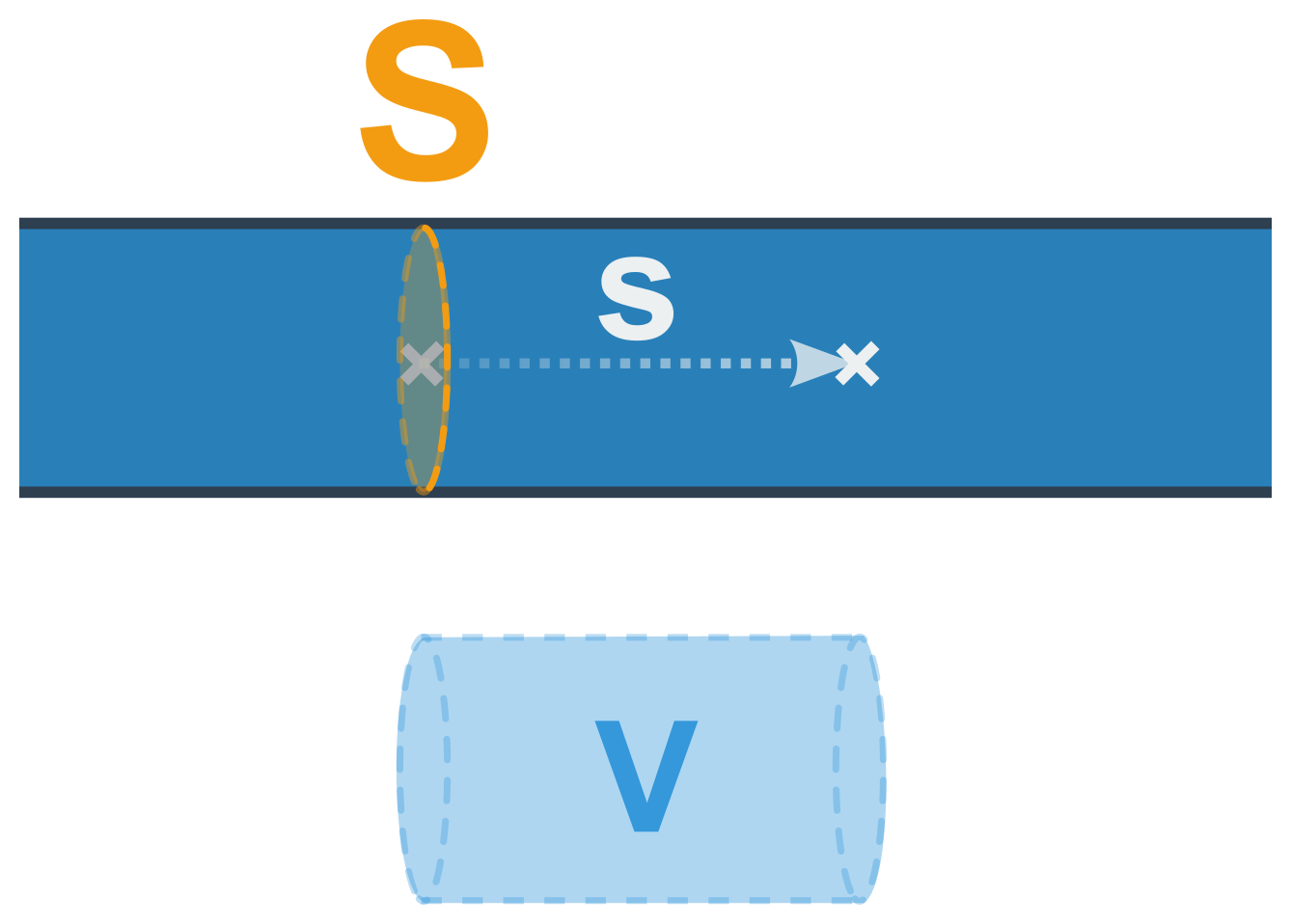
Víme přitom, že \frac{s}{t} je klasická definice rychlosti, tedy i rychlosti proudění v. Pak můžeme průtok zapsat ekvivalentní rovnicí:
Q_V=S\cdot v
Příklad: Lipno
Jaký průtok vody míří na turbínu vodní elektrárny Lipno I, pokud v její 15 m² přívodní šachtě proudí voda rychlostí 2 m/s?
- Známe S i v a to v základních jednotkách.
- Stačí tedy dosadit dosadit do Q_V=S\cdot v
- Q_V=15\cdot 2 \,\mathrm {m^3/s}=30 \,\mathrm {m^3/s}
- Průtok je 30 \,\mathrm {m^3/s}.
Protože jsou kapaliny nestlačitelné, musí být průtok Q_V v uzavřeném plném potrubí všude stejný (jinak by se někde musela hromadit).
Pokud tedy porovnáme dvě místa (Q_{V{,}1}=Q_{V{,}2}) a dosadíme za jednotlivé průtoky, vznikne známý vzorec rovnice kontinuity:
S_1\cdot v_1=S_2\cdot v_2
Příklad: stále stejně tlusté potrubí
Jak se mění rychlost ideální kapaliny při průchodu stále stejně tlustým potrubím?
- Nabízí se odpověď „všude stejná“. Ověříme to.
- Pro dvě místa v trubici platí S_1\cdot v_1=S_2\cdot v_2.
- Oba průřezy S_1 i S_2 jsou stejné, označme je tedy jednotně jako S.
- Máme S\cdot v_1=S\cdot v_2. V této rovnici můžeme krátit S.
- Dostaneme v_1=v_2. Tedy i rychlosti musí být stejné.
Příklad: přechod potrubí na třikrát větší průřez
Jak se změní rychlost ideální kapaliny při rozšíření potrubí na trojnásobný průřez?
- Nejprve přiřadíme jednotlivým místům v potrubí označení: užší část bude (1) a širší (2).
- Platí S_1\cdot v_1=S_2\cdot v_2.
- Víme že S_2=3\cdot S_1. Dosadíme to do rovnice.
- S_1\cdot v_1=3\cdot S_1\cdot v_2. Můžeme krátit S_1.
- Dostaneme v_1=3\cdot v_2. Hledáme ale rychlost v_2.
- Dělíme tedy 3 a dostaneme v_2=\frac{1}{3} v_1.
- Rychlost tedy bude třetinová.
Zajímavosti
- Přibližně platí i pro volně proudící kapalinu (řeka a její koryto).
- Někdy přibližně platí pro plyny (jsou stlačitelné).
- Obdobné rovnice kontinuity platí například i v elektřině (1. Kirchhoffův zákon).
- Rovnice V=S\cdot s je spolehlivá jen pro malé s (mohl by se změnit průměr trubice). Naštěstí rovnice Q_V=S\cdot v je už platná obecně.
Bernoulliho rovnice
Bernoulliho rovnice popisuje souvislost mezi tlakem p v kapalině (o hustotě \rho) a rychlostí jejího proudění v. Podél jedné proudnice platí:
\frac{1}{2}\rho v^2+p = \mathrm{konst.}
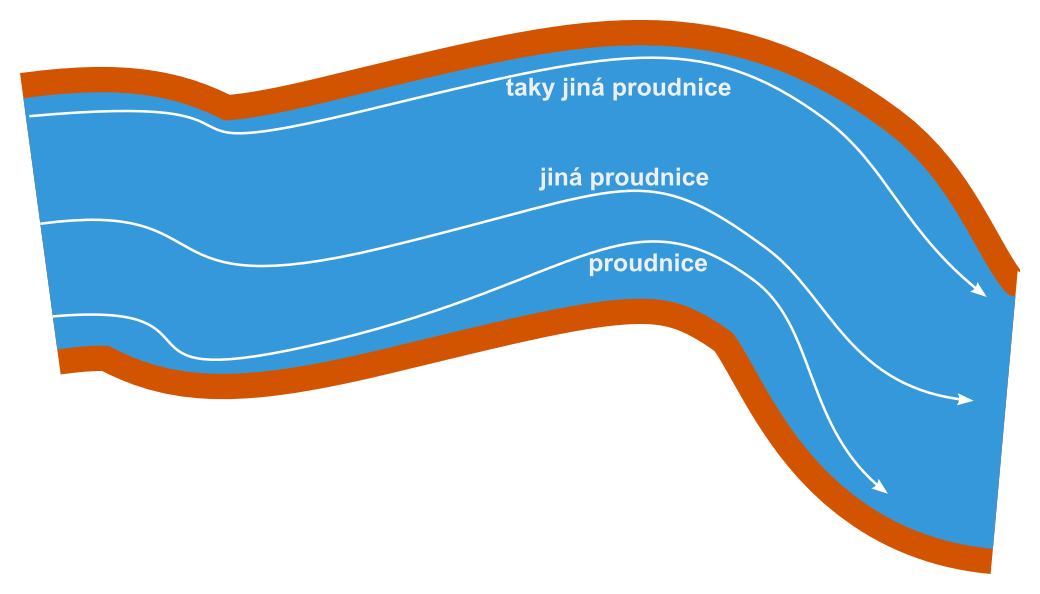
Příklad: Zužující se trubice
Rychlost se v užší části trubice zvedla na dvojnásobek. Jak se tam změní tlak kapaliny?
- Protože se zvedla rychlost v, zvedla se i hodnota \frac{1}{2}\rho v^2 (\rho je u kapalin konstantní).
- Podle Bernoulliho rovnice má ale být \frac{1}{2}\rho v^2+p stále stejné. Musí tedy klesnout druhá část součtu – p.
- Odpověď tedy zní, že tlak klesne.
Pro dvě místa na téže proudnici tedy platí (pro konstantní hustotu):
\frac{1}{2}\rho v_1^2+p_1 = \frac{1}{2}\rho v_2^2+p_2
Příklad: Rychlost proudění podle změny tlaků
Voda proudí potrubím 1 m/s a má v něm tlak 5000 Pa. Jaký je tlak v části, kde voda proudí rychlostí 2 m/s?
- Platí \frac{1}{2}\rho v_1^2+p_1 = \frac{1}{2}\rho v_2^2+p_2.
- Známe všechno (voda má \rho=1000\,\mathrm{kg/m^3}) kromě p_2. To je naše neznámá, kterou musíme vyjádřit.
- Tlak p_2 osamostatníme odečtením \frac{1}{2}\rho v_2^2 od obou stran rovnice.
- Dostaneme: p_2=\frac{1}{2}\rho v_1^2+p_1-\frac{1}{2}\rho v_2^2
- Dosadíme: p_2=\frac{1}{2}1000\cdot 1^2+5000-\frac{1}{2}1000\cdot 2^2\,\mathrm{Pa}=500\cdot 1+5000-500\cdot 4\,\mathrm{Pa}=3500\,\mathrm{Pa}
- Tlak tedy klesne na 3500 Pa.
Pro jednoduchost obvykle definujeme Bernoulliho rovnici pro vodorovnou uzavřenou trubku.
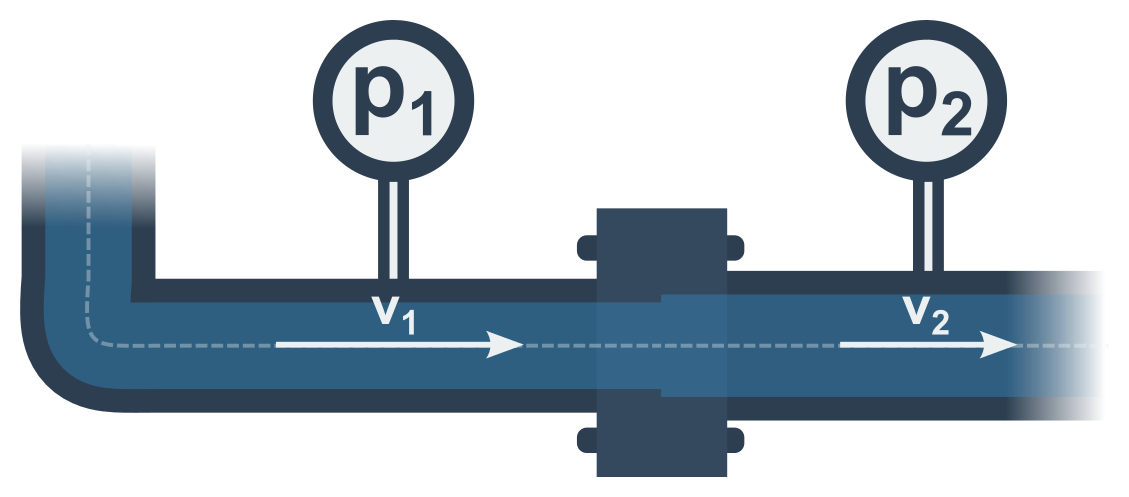
Jak by to bylo pro nevodorovnou trubku?
Pro nevodorovnou trubku bychom museli do rovnice započítávat i hydrostatický tlak p_h.
Bernoulliho rovnice vlastně říká, že zvýšením rychlosti proudění poklesne tlak. Tento princip platí i pro libovolné neturbulentní proudění kapaliny nebo plynu. Matematický vzorec sice v takovém případě neplatí přesně, ale jako odhad se hodí.
Tohoto principu se využívá v řadě případů, kde chceme vůči okolnímu prostředí vytvořit podtlak (fixírka, některé typy vývěv, profil křídla letadel).
Zajímavosti
Bernoulliho rovnice je vlastně rovnice zachování energie na jednotku objemu. Po vynásobení objemem je to ještě patrnější – získáte \frac{1}{2}m v^2 (kinetická energie) a p\cdot V=p\cdot S\cdot s=F\cdot s (práce/potenciální energie).
Vytékání kapaliny malým otvorem
Pomocí Bernoulliho rovnice (\frac{1}{2}\rho v_1^2+p_1 = \frac{1}{2}\rho v_2^2+p_2) můžeme odvodit rychlost tryskání vody z (malého) otvoru v nějaké nádobě.
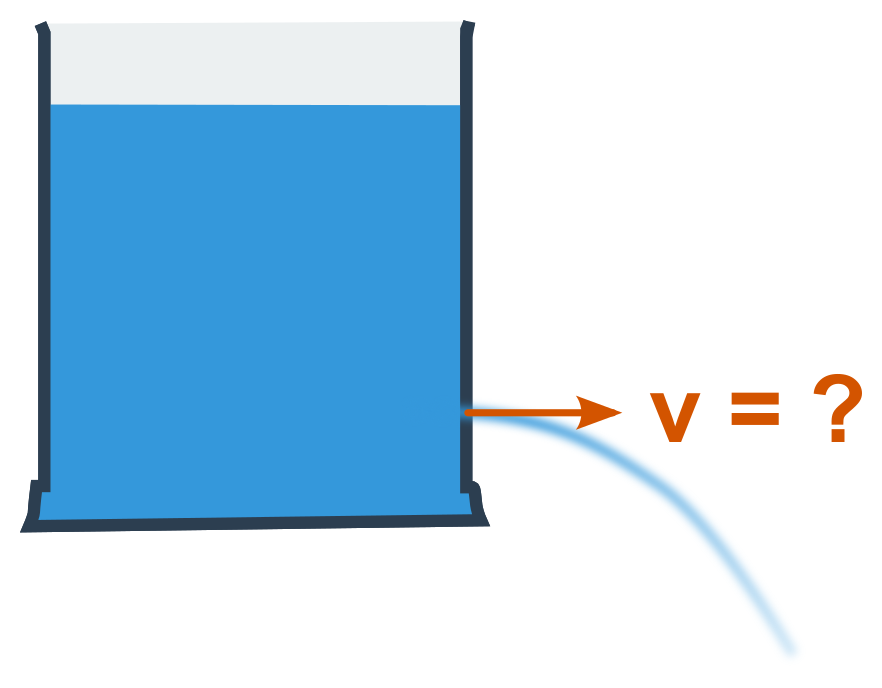
Zevnitř (index 1) je rychlost prakticky nulová a vně (index 2) je zase nulový tlak (pokud od obou stran odečteme atmosférický tlak). Po dosazení těchto nul do rovnice výše dostaneme p_1 = \frac{1}{2}\rho v_2^2.
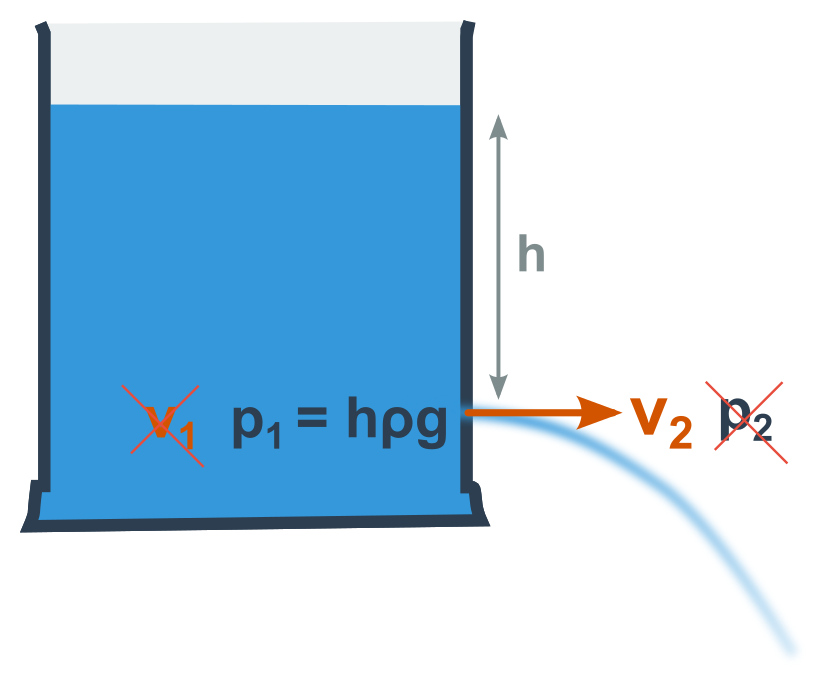
Tlak p_1 je vlastně hydrostatický tlak v nádobě (h\rho g) a rychlost zůstala jen jedna, nemusíme ji tedy indexovat. Máme h\rho g=\frac{1}{2}\rho v^2, z čehož vyjádříme rychlost:
v = \sqrt{2 h g}
Příklad: dvojnásobná hloubka
- Bude z otvoru v dvojnásobné hloubce nebude stříkat voda dvakrát rychleji?
- Podle vzorce v = \sqrt{2 h g} závisí rychlost na odmocnině z hloubky.
- Pokud tedy změníme h na 2h, dostaneme v = \sqrt{2\cdot 2 h g}= \sqrt{2}\cdot \sqrt{2 h g}.
- Rychlost tedy bude jen \sqrt 2-krát větší.
Příklad: stav beztíže
- Jaká bude rychlost stříkání vody z děravé lahve ve stavu beztíže?
- Ve stavu beztíže je g nulové.
- Do v = \sqrt{2 h g} tedy dosazujeme nulu. A součin s nulou je nulový celý.
- A odmocnina z nuly je nula. Rychlost tedy bude nulová – ve stavu beztíže voda samovolně nevytéká.
Deformace pevných látek
Způsoby deformace tělesa
- tahem – dvojice sil, směřují ven z tělesa, leží na jedné přímce (těleso se natahuje):

- tlakem – dvojice sil, směřují do tělesa, leží na jedné přímce (těleso se stlačí):

- smykem – dvojice sil opačných směrů, leží na různých přímkách (těleso se zkosí):

ohybem – dvě síly působící jedním směrem, třetí síla v opačném směru, na různých přímkách (těleso se prohne):
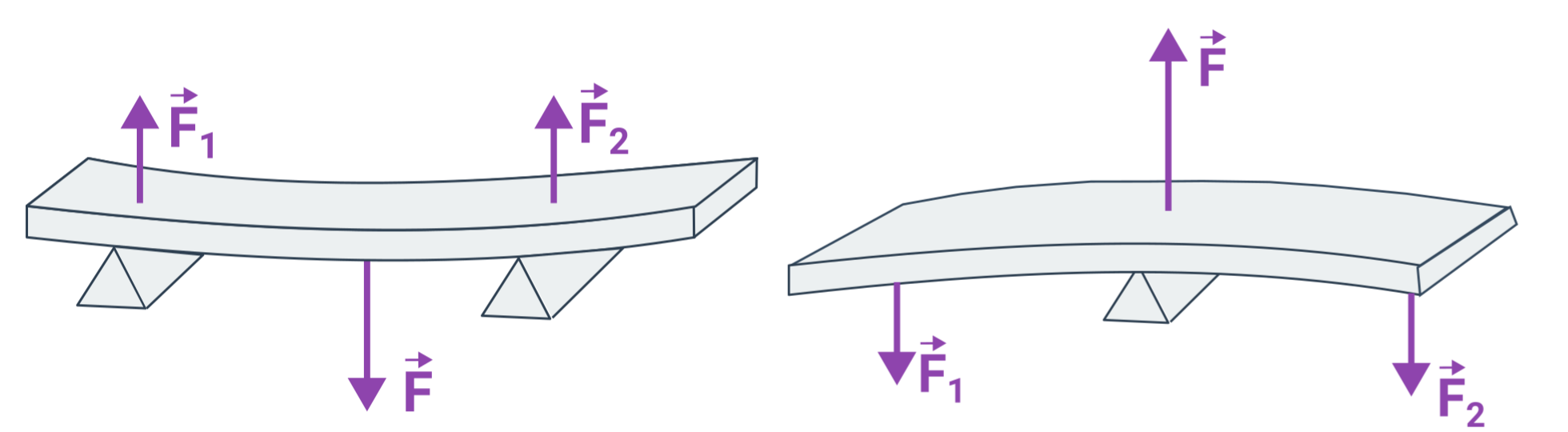
kroucením – dvě dvojice sil, otáčejí těleso v různých místech opačnými směry (těleso se zkroutí):
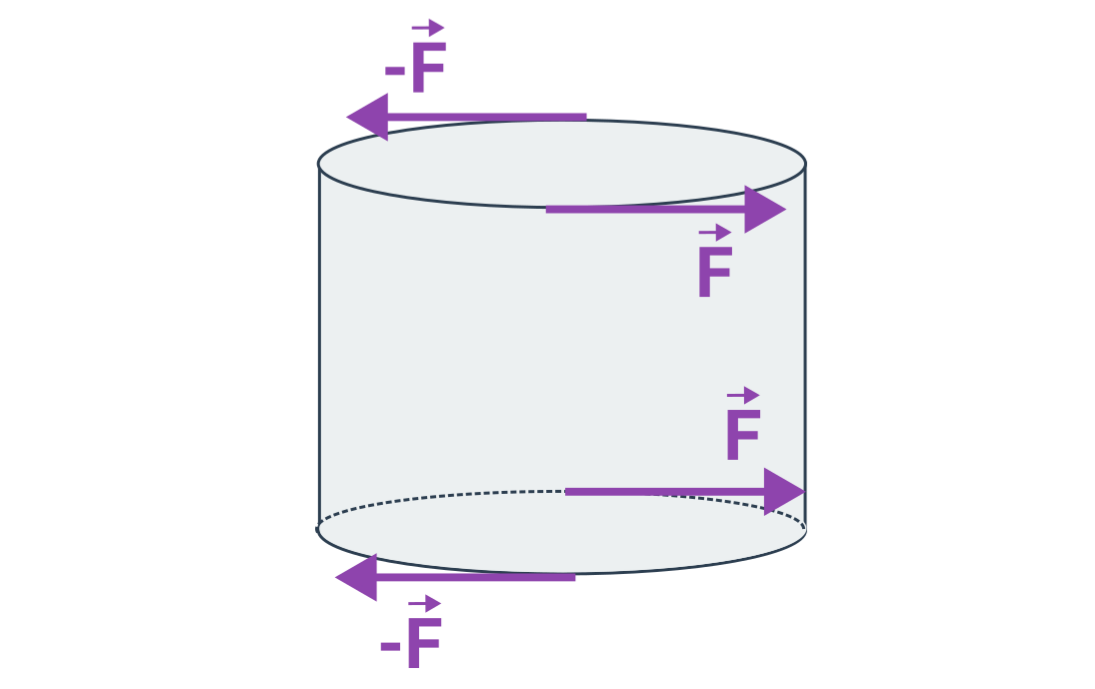
Normálové napětí \sigma_\mathrm{n}
Popisuje napětí v materiálu. Definujeme jej jako podíl síly F a průřezu tělesa S, na které síla působí.
\sigma_\mathrm{n} = \frac{F}{S}
V přeneseném významu odpovídá \sigma_\mathrm{n} tlaku, což naznačuje i pravá strana vzorce (shodná s obecnou definicí tlaku). I jednotkou je tedy pascal.
Hookův zákon
Když se deformací těleso prodlouží (nebo zkrátí), můžeme tu změnu popsat pomocí bezrozměrné veličiny relativní prodloužení \varepsilon. Tedy kolikanásobně se těleso prodlouží. Matematicky je to změna délky \Delta l děleno původní délka l_0 tělesa:
\varepsilon = \frac{\Delta l}{l_0}.
Příklad: Prodloužení tyče
Gumové lano jsme z původních 2 metrů natáhli na 2,4 m. Jaké je \varepsilon?
- Původní délka l_0 je 2 m.
- Změna délky \Delta l je rozdíl mezi 2,4 m a 2 m. Tedy 0,4 m.
- Dosadíme do \varepsilon = \frac{\Delta l}{l_0}=\mathrm{\frac{0{,}4\,m}{2\,m}}=0{,}2
- Relativní prodloužení je tedy 0,2 (nebo také 20 procent).
Hookův zákon udává, že normálové napětí \sigma_\mathrm{n} je přímo úměrné tomuto relativnímu prodloužení. Tedy:
\sigma_\mathrm{n} = E\cdot\varepsilon
Konstanta úměrnosti E je tzv. Youngův modul pružnosti (jednotka pascal). Hookův zákon ale platí jen pro menší normálová napětí (po mez úměrnosti \sigma_\mathrm{u}).
Příklad: Napětí v ocelové tyči
Jaké je napětí v ocelové tyči s E=200\,\mathrm{GPa}, když se kvůli němu prodloužila o desetinu své původní délky?
- Relativní prodloužení \varepsilon je desetina, tedy 0,1.
- E máme zadáno, to je 200 GPa, tedy 200 miliard Pa.
- Dosadíme do \sigma_\mathrm{n} = E\cdot\varepsilon
- Dostaneme 200 miliard krát 0,1.
- Napětí v tyči \sigma_\mathrm{n} je tedy 20 miliard Pascalů.
Jak na relativní prodloužení lana se znalostí působící síly?
Známe velikost působící síly F, materiál tělesa (tedy i modul pružnosti v tahu) a průřez materiálu S, jak se lano prodlouží?
- Využijeme definice normálového napětí (\sigma_\mathrm{p} = \frac{F}{S}) i Hookova zákona (\sigma_\mathrm{p} = E\cdot\varepsilon), dosadíme za \sigma_\mathrm{p}, potom \frac{F}{S} = E\cdot\varepsilon.
- Obě dvě strany podělíme modulem pružnosti E a obdržíme hledaný výsledek \varepsilon = \frac{F}{S\cdot E}.
Křivka deformace
Deformace pevné látky popisuje tzv. křivka deformace 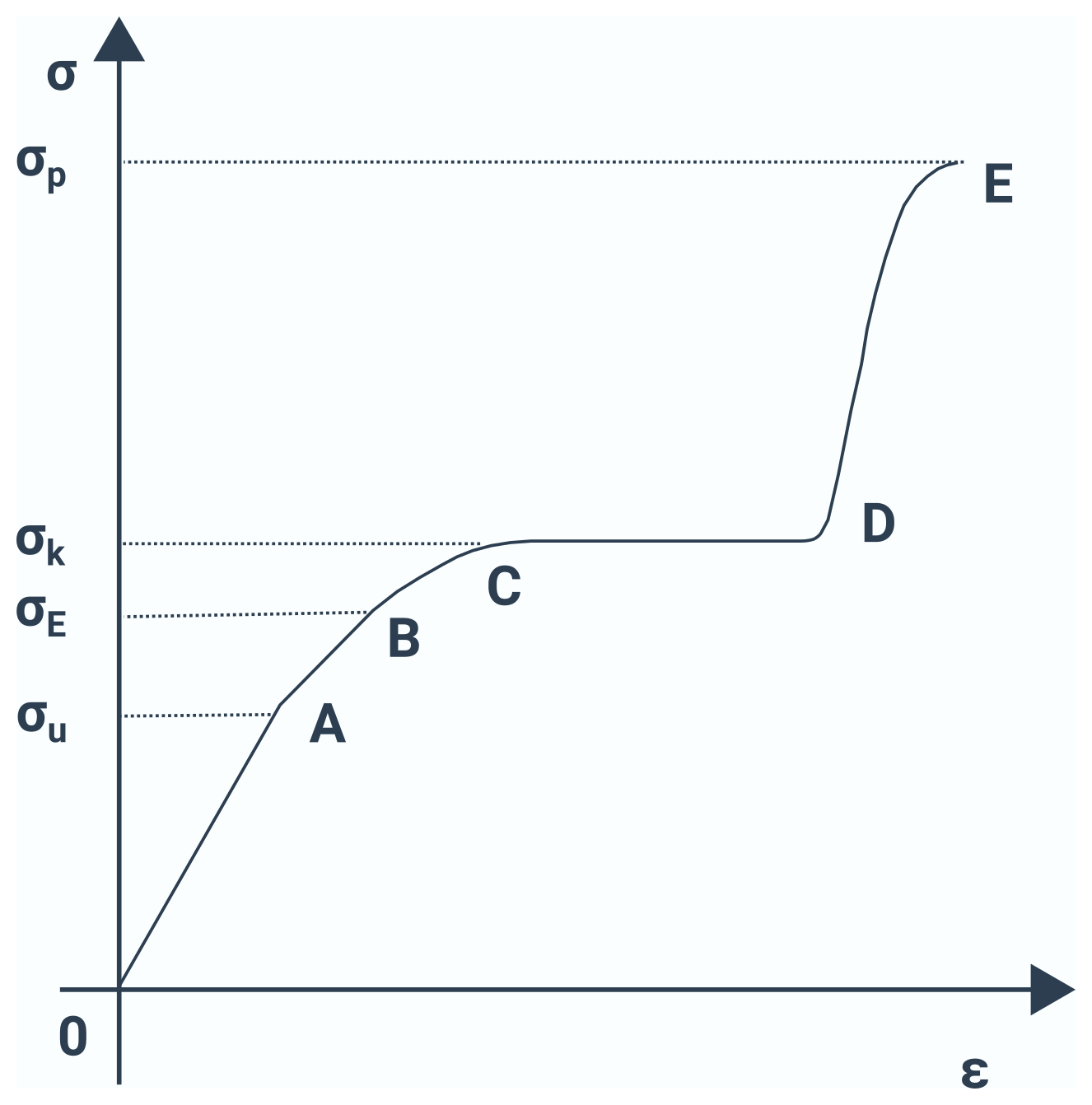 na křivce se nachází několik charakteristických bodů a intervalů
na křivce se nachází několik charakteristických bodů a intervalů
- 0B – pružná deformace (\sigma_\mathrm{u} je mez platnosti Hookova zákona a \sigma_\mathrm{E} mez pružnosti)
- BC – nepružná deformace (\sigma_\mathrm{k} je mez kluzu)
- CD – tečení materiálu
- DE – zpevnění
- oblast za E – těleso již nedrží pohromadě (\sigma_\mathrm{p} je mez pevnosti)
Vlnění: pojmy
Vlnění si představíme intuitivně podle vln na vodě. Obecně je to kmitání (nějaké veličiny), které se šíří do prostoru.
Dělíme jej podle směrů šíření a výchylky:
- podélné – výchylka je rovnoběžná se směrem šíření (např. zvukové vlny, zhušťování a ředění)
- příčné – výchylka je kolmá na směr šíření (např. struna na kytaře, vypadají tak i vlny na vodě)
- ani jedno – výchylka je vůči směru šíření orientovaná libovolně (skutečné vlny na vodě)
Vlny mají stejně jako kmity frekvenci f (kolikrát za sekundu jedním místem prokmitnou) a periodu T (čas, po kterém se začne vlna opakovat). Platí:
f\cdot T=1
Navíc mají vlnovou délku \lambda (vzdálenost, po jaké se začne vlna opakovat). Vlna se šíří rychlostí v. Platí:
v=\lambda \cdot f
Vlnová délka má jednotku m, a rychlost má jednotku m/s.
NahoruZvuk: základy
Zvuk je vlnění. Tedy, zvuková vlna je mechanická vlna, která se šíří látkovým prostředím (např. vzduchem, vodou). Vzniká, když nějaké těleso v tomto prostředí kmitá.
Podle toho, zda je kmitání periodické, můžeme rozlišovat tóny a hluky.
Tón
Zvuková vlna tónu je periodická – je v ní vzor, který se pravidelně opakuje. Jak často se opakuje, nám udává frekvence.
Pravidelně se opakující vzor
Vzor, který se opakuje, může vypadat třeba takto:

Tóny rozdělujeme na jednoduché a složené. Jednoduché tóny můžeme popsat harmonickou funkcí.
Harmonická funkce
Vysvětlit, co je harmonická funkce, je složité. My si vystačíme s tím, že příkladem harmonické funkce je funkce sinus.
Složené tóny lze vytvořit kombinací několika jednoduchých tónů, které se sečtou. Popisují je složitější funkce.
Příklad: Kombinace jednoduchých tónů
Jak můžeme složený tón rozložit na několik jednoduchých tónů?

- oranžová a modrá křivka odpovídají jednoduchým tónům
- fialová křivka odpovídá složenému tónu, který vznikl kombinací modrého a oranžového
Složené tóny většinou najdeme v hudbě (zpěv, zvuk flétny, klavíru nebo klarinetu), zatímco jednoduché tóny umí vytvořit počítač nebo ladička. Složené tóny od sebe rozlišíme sluchem, díky tomu že obsahují zastoupení různých tónů vyšších frekvencí.
Příklady tónu:
- vyslovení samohlásky, např. samohlásky a, e, o, i (naše hlasivky kmitají pravidelně)
- hra na flétnu
- drnknutí na kytaru
- zvuk vrtačky (pravidelně se opakuje)
- bzučení hmyzu (moucha periodicky kmitá křídly)
Hluk
Zvuková vlna hluku není periodická. Tím, že je nepravidelná, nemá přesnou frekvenci (počet opakování vzoru za sekundu). Speciálním případem hluku je šum (náhodné změny tlaku ve vzduchu).
Příklady hluku:
- vyslovení souhlásky, např. souhláska r, t, z (naše hlasivky kmitnou nepravidelně)
- kýchnutí
- zvuk rozbité sklenice
- výstřel
- štěrchání rumbakoulemi (přesto že to je hudební nástroj, nevydávají pravidelný zvuk)
Vlastnosti zvuku
Stejně jako jiné druhy vlnění má zvuk frekvenci, periodu, rychlost šíření a vlnovou délku.
frekvence f
- vyjadřuje, kolikrát se vlna zopakuje za jednu sekundu
- jednotka frekvence je hertz (Hz), počet hertzů odpovídá počtu kmitů za sekundu
- lidé slyší pouze zvuku z omezeného rozsahu frekvencí
jednotka frekvence
1 \,\mathrm{ Hz} = \frac{1}{\mathrm s} = 1 \,\mathrm{ s}^{-1} Jeden hertz znamená, že předmět kmitne jednou za sekundu – takovou frekvenci mají třeba běžné hodiny (s vteřinovou ručičkou). Zvuková vlna tónu s frekvencí 440 Hz se za sekundu zopakuje čtyři sta čtyřicetkrát!
perioda T
- vyjadřuje, jak dlouho trvá jedno kmitnutí
- měříme ji v sekundách
- platí: T\cdot f = 1, tedy čím je perioda větší, tím je frekvence menší a naopak
To dává smysl, když si představíme, co vlastně frekvence a perioda znamenají. Pokud je vysoká frekvence, kmitá vlna rychle. A čím rychleji kmitá, tím víckrát stihne kmitnout za jednu sekundu – její perioda tedy bude kratší.
rychlost šíření v
- vyjadřuje, jak rychle se zvuk šíří daným prostředím
- vyjadřujeme ji v metrech za sekundu (m/s)
vlnová délka λ
- vzdálenost, kterou zvuk v prostoru urazí za dobu jedné periody T (za jedno kmitnutí)
- odpovídá vzdálenosti mezi dvěma po sobě jdoucími místy s nejvyšším tlakem (nejvíce nahuštěný vzduch)
- platí v = \lambda \cdot f
Vlnová délka se tedy při stejné frekvenci mění podle toho, v jakém prostředí se zvuk šíří. Slyšitelné zvuky mají ve vzduchu vlnovou délku mezi 2 cm a 20 m, ve vodě je víc než čtyřikrát větší.
Výška, hlasitost, barva
Mezi základní vlastnosti, které jsou specifické pro zvuk, patří výška, hlasitost, barva a délka.
výška
Výšku tónu vnímáme subjektivně, je dána základní frekvencí zvuku. Čím je frekvence vyšší, tím vyšší zvuk slyšíme.
Vysokým zvukům tak odpovídají vlny s vysokou rychlostí kmitání nebo také krátkou vlnovou délkou a krátkou periodou.
hlasitost
Hlasitost souvisí s amplitudou zvukové vlny (jak moc se změní tlak vzduchu nebo intenzita zvukové vlny) – čím je změna vyšší, tím hlasitější zvuk slyšíme. Vnímáme ji subjektivně.
Fyzikálně hlasitosti odpovídá veličina zvaná hladina intenzity zvuku. Hladina intenzity zvuku je bezrozměrná (podobně jako např. procento). Využíváme pro ni ale jednotku Bel (nebo častěji její násobek – decibel (dB)), která vyjadřuje logaritmus poměru dvou hodnot: naměřené hladiny intenzity zvuku k hladině intenzity nejtiššího slyšitelného zvuku. Nejtišší slyšitelný zvuk se nazývá práh slyšení (0 dB). Nad 130 dB se pak nachází práh bolesti.
Intenzita zvuku a hladina intenzity zvuku
Hladina intenzity zvuku (označujeme L) pro zvuk o intenzitě I se spočítá jako L= 10 \mathrm{log}\frac{I}{I_0} kde I_0 je intenzita prahu slyšení, tedy intenzita nejtiššího zvuku, který člověk dokáže slyšet.
A co je to vlastně ta intenzita?
- intenzita souvisí s energií zvukové vlny, vyjadřuje, jakou energii přenese zvuková vlna
- intenzita klesá čím dále jsme od zvukového zdroje, protože zvuk část své energie ztrácí při průchodu prostředím
Decibel je logaritmická jednotka. Lidské ucho totiž vnímá i velké změny podnětů (například nárůst změny tlaku ve vzduchu) jako malou změnu počitku. Pokud se intenzita změní stokrát, hladina intenzity se zvedne o dvacet decibelů.
hlasitost a výška – příklad
- zvukové vlny v grafu se liší frekvencí i amplitudou
- oranžová vlna má vyšší frekvenci než modrá vlna, slyšeli bychom ji tedy jako vyšší
barva
Barva zvuku souvisí s tvarem zvukové vlny. Díky barvě zvuku od sebe můžeme odlišit lidské hlasy nebo tóny různých hudebních nástrojů, přestože vydávají zvuk stejné frekvence.
Složené tóny kromě základní (nejnižší) frekvence obsahují také směs dalších (tzv. vyšších harmonických) frekvencí. Vyšší harmonické frekvence jsou celočíselné násobky základní frekvence. V tónech různé barvy jsou vyšší harmonické frekvence zastoupené s různou intenzitou, ovlivňují tvar zvukové vlny a tím i barvu tónu.
výška a barva – příklad
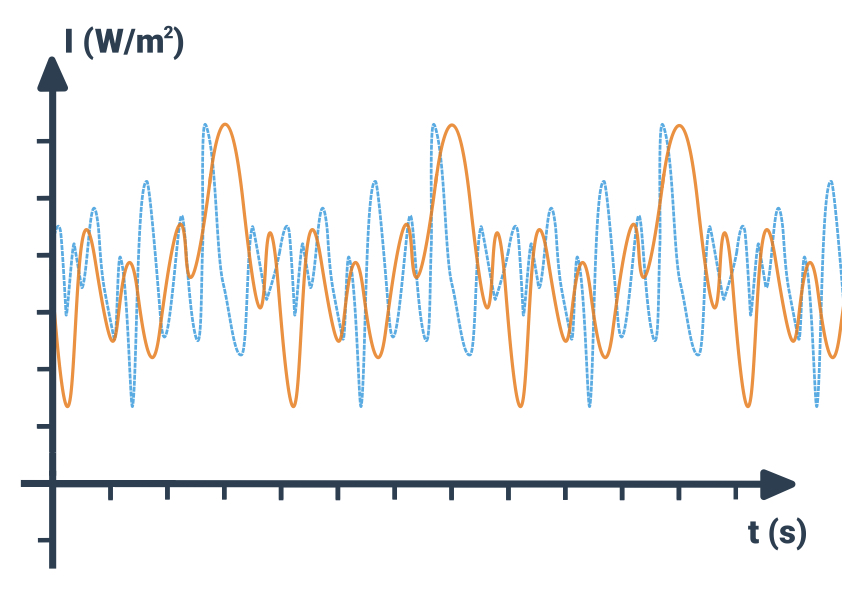
- zvukové vlny v grafu mají stejnou frekvenci, takže bychom je slyšeli stejně vysoko
- liší se ale tvarem vlny – barvou
Rychlost zvuku a šíření zvuku
Zvuk je mechanické vlnění, ke svému šíření potřebuje látkové prostředí (např. voda, vzduch, pevná látka). Na rozdíl od světla (elektromagnetické vlnění) se tedy zvuk nešíří ve vakuu.
mechanické a elektromagnetické vlnění
Mechanické vlnění se šíří prostředím, kde jsou částice. Kmitání jedné částice se díky vzájemným vazbám přenáší na další částici a tak dál. Mechanické vlnění jsou třeba vlny na vodní hladině, kmitání tyče, do které jsme udeřili, nebo zvuk.
Elektromagnetické vlnění ke svému šíření částice nepotřebuje. Jedná se vlastně o kmity elektrického a magnetického pole (časově proměnné silové pole). Elektromagnetické vlnění různé vlnové délky je viditelné světlo, rentgenové záření, mikrovlnné záření nebo rádiové vlny.Čím jsou v daném prostředí částice k sobě blíž a čím pevnější mají vazby, tím rychleji se zvuk šíří. Ve vzduchu (rychlost zvuku ~340 m/s) se tedy šíří pomaleji než ve vodě (~1500 m/s) nebo třeba v oceli (~5000 m/s).
Šíření zvuku ve vzduchu
- Zvuková vlna se šíří všemi směry jako změna tlaku. Šíření zvuku odpovídá kmitání částic, které se k sobě přibližují a pak se zase vzdalují.
- Zvuk ve vzduchu je podélné vlnění. To znamená, že částice kmitají ve směru šíření vlny.
- Rychlost zvuku závisí na teplotě vzduchu: čím je vzduch teplejší, tím rychleji se zvuk šíří. Tato závislost je v rozumném rozsahu teplot (rozuměj zhruba od -100 °C do 100 °C) přibližně lineární.
- Pokud považujeme vzduch za ideální plyn, nezávisí rychlost šíření zvuku na tlaku.
- Zvuk se taky šíří nepatrně rychleji ve vlhkém vzduchu (třeba při bouřce), rychlost závisí i na složení vzduchu (např. v lehčích plynech se šíří rychleji než v těžších).
Odraz zvuku
Když zvuková vlna narazí na překážku, část se odrazí. Podle toho, o jakou překážku se jedná, odrazí se více nebo méně zvuku – tvrdé a hladké povrchy (skála, dlaždice) vedou k silnějšímu odrazu, zatímco měkčí povrchy (molitan, koberce) více zvuku pohltí. Proto když si zpíváme v koupelně, zvuk se hezky “rozléhá” – odráží se od hladkých povrchů.
Ozvěna a dozvuk
- Pokud je překážka, od které se zvuk odráží, plochá a velká (např. skalní stěna, rozměrná budova), může vzniknout ozvěna nebo dozvuk.
- Pokud se odražený zvuk vrátil za více než 0,1 sekundy, mluvíme o ozvěně. Desetina sekundy je totiž čas, který zhruba trvá vyslovit jednu slabiku. Takovou ozvěnu pak tedy slyšíme jako opakování původního zvuku, například poslední slabiky.
- Pokud se odražený zvuk vrátí za méně než desetinu sekundy, jedná se o dozvuk. Lidské ucho v takovém případě nezvládne jasně rozlišit původní a odražený zvuk.
Jak musí být vzdálená taková překážka, aby vznikla ozvěna?
Zvuk se ve vzduchu šíří rychlostí asi 340 m/s a chceme vědět, jak daleko je překážka, od které se vrátí za 0,1 s.
Protože se zvuk šíří rovnoměrně, můžeme využít vztah pro výpočet dráhy:
s = v\cdot t = 340 \cdot 0,1 = 34\,\mathrm{m}, kde t bude čas a v rychlost zvuku.
Celková dráha s zahrnuje cestu k překážce a zpátky (34 m). Abychom získali vzdálenost od překážky, musíme ji ještě podělit dvěma.
Aby vznikla ozvěna, musí být překážka vzdálená nejméně 17 metrů.Využití odrazu zvuku
- Odraz zvuku využívají v přírodě například delfíni nebo netopýři při lovu kořisti (echolokace).
- Lidé tento postup napodobili – například k měření hloubky moře využívají sonar.
- Odrazu zvuku se také využívá například při kontrole materiálů nebo při měření vzdálenosti pomocí ultrazvukových měřičů.
Ohyb zvuku
Zvuk se může šířit i za překážkami. Díky ohybu zvuku slyšíme, když někdo mluví za rohem, přestože jej nevidíme. Ohyb zvuku je výraznější u překážek, které mají podobnou velikost jako vlnová délka zvuku. Zvuky vysokých frekvencí se tlumí snáz než nízkofrekvenční zvuky. Proto ve velké vzdálenosti slyšíme hrom už jen jako hluboké dunění.
NahoruUltrazvuk, infrazvuk a sluch
Lidé slyší zvuky z omezeného rozsahu frekvencí – 16 Hz až 20 000 Hz.
Pokud má nějaká zvuková vlna frekvenci nižší než 16 Hz, jedná se o infrazvuk. A naopak vlna o frekvenci vyšší než 20 000 Hz je zase ultrazvuk. S věkem postupně ztrácíme citlivost k vysokým frekvencím (horní hranice toho, co slyšíme, klesá např. na 16 000 Hz).
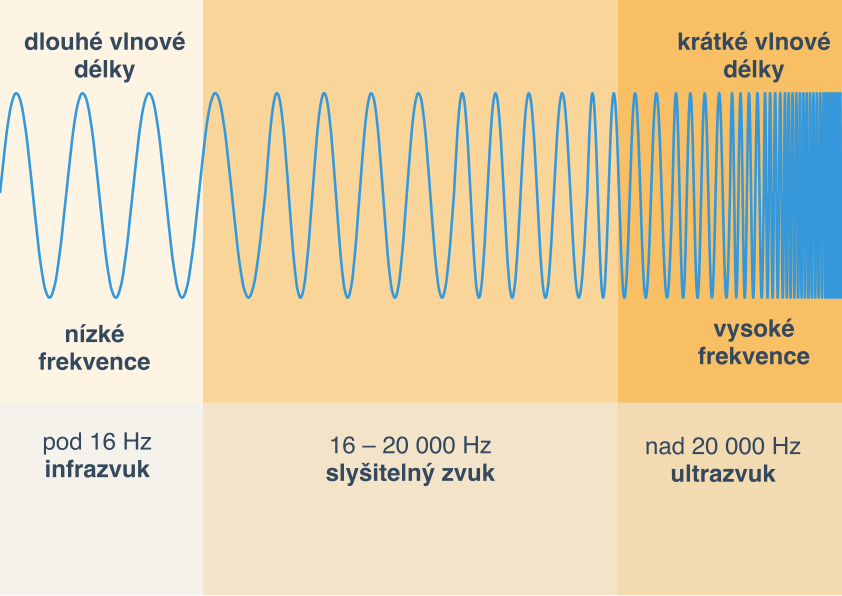
Přestože lidé infrazvuky a ultrazvuky neslyší, některá zvířata je slyšet mohou. Sloni využívají infrazvuky ke komunikaci, netopýři zase využívají ultrazvuk při orientaci v prostoru a lovu kořisti (tzv. echolokace). A tak dále:
Infrazvuk se využívá například:
- k predikci zemětřesení (seismograf) nebo sopečné aktivity
- k sledování pohybu slonů
Ultrazvuk se využívá například:
- ke kontrole materiálů
- k vyšetřování měkkých tkání ve zdravotnictví (sonografie)
- k čištění
Zvuk v hudebních nástrojích
Na světě existují stovky hudebních nástrojů. Tóny v nich vznikají různými způsoby, podle toho nástroje dělíme na různé druhy.
Bicí nástroje (blanozvučné a samozvučné)
- Jsou to například: triangl, kastaněty, dřívka, xylofon, zvon, …
- Zvuk v nich vzniká buď rozkmitáním membrány (např. buben) nebo samotného nástroje (např. gong, zvon).
- Čím je membrána tenčí a napjatější, tím vyšší základní tón buben vydává.
Většina bicích nástrojů má jednu základní frekvenci, ale například u tympánů může hudebník sešlápnutím pedálu napínat nebo povolovat membránu bubnu, čímž zvyšuje nebo snižuje základní frekvenci. U xylofonu získáme různé tóny zase úderem do různě dlouhých kamenů.
Strunné nástroje
- Patří mezi ně například: kytara, banjo, ukulele, housle, viola, violoncello, kontrabas, klavír, harfa, cimbál, …
- Zvuk vzniká rozechvěním struny, zesiluje se často v rezonanční dutině (např. tělo kytary či houslí).
Strunné: smyčcové (housle, viola, violoncello, kontrabas)
Chvění struny vzniká díky tření mezi smyčcem a strunou. Pro zvýšení tření se často smyčec potírá kalafunou.
Strunné: úderné (klavír, cimbál)
Klavír: Při stisknutí klávesy udeří kladívko do struny, ta pak rozkmitá rezonanční desku, která tón zesílí.
Cimbál: Při hře na cimbál rozechvívá struny hudebník tím, že do nich udeří paličkou.
Strunné: drnkací (kytara, harfa, ukulele)
Kytara, ukulele: Hmatník a pražce využívá muzikant pro zkrácení struny, díky tomu zní vyšší tóny. Nástroj se dá také ladit kolíky, které napínají nebo povolují strunu – napjatější struna kmitá s vyšší frekvencí.
Harfa: Výšku tónu ovlivňuje hudebník pedály, které zkracují kmitající část struny.
Dechové nástroje
- V řadě dechových nástrojů může muzikant měnit výšku tónu tím, že prodlužuje nebo zkracuje vzduchový sloupec. Například ve flétně mění hráč délku sloupce zakrýváním nebo odkrýváním otvorů prsty.
- Čím je sloupec kratší (např. při hře na flétnu nezakrývám prstem žádné otvory), tím je tón vyšší.
- Jiné nástroje se dají prodloužit, aby hrály hlubší tóny (např. klarinet nebo trubka).
Flétna: Tón ve flétně vzniká nárazem proudu vzduchu na hranu otvoru. To vytváří opakující se víry, které rozkmitají vzduchový sloupec ve flétně a vzniká stojaté vlnění.
Trubka, tuba: Zdrojem kmitání jsou hudebníkovy rty, mezi kterými vyfukuje tenký proud vzduchu. Pro hru na tyto nástroje musí mít hudebník správný nátisk – kombinace napětí rtů a tlaku vzduchu, který mezi ně hráč vpouští. Plechovým dechovým nástrojům (trubka, tuba, lesní roh, pozoun a další) se také říká nástroje žesťové.
Saxofon, klarinet: Vzduch, který hudebník fouká do nástroje, rozkmitá plátek, který rozkmitá vzduch v nástroji.
Hoboj: V hoboji jsou plátky dva, muzikant fouká mezi ně. Díky tomu se přibližují a oddalují, čímž vznikají kmity.
Varhany: Varhany mají ke každé klávese připojenou píšťalu (dřevěnou nebo kovovou trubici), do které vhání vzduch měchy.
Elektrické nástroje
- Řada nástrojů má také svou elektrickou variantu, ve které se elektrické signály převádějí na akustické.
- Například v elektrické kytaře zaznamenávají snímače (malé cívky) změny v magnetickém poli, které vznikají díky kmitání struny s ocelovým jádrem. Kmity jsou pak převedeny do reproduktorů.

